08届高考数学第一次模拟考试试题
(命题人 杨帆)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,试卷满分150分,考试用时120分钟。
☆祝你考试顺利☆
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案填在答题卷上。
1.(理)复数![]() =
=
(A)0 (B)![]() (C)1 (D)
(C)1 (D)![]()
(文)若集合A={x∣2},B={x∣x2-3x=0},则集合AB=
(A){3} (B){0} (C){0,2} (D){0,3}
2.函数 y=(x0)的反函数是
(A)y=(x) (B)y=-(x)
(C)y=(x0) (D)y=-(x0)
3.sin15°cos165°的值是
(A)![]() (B)
(B)![]() (C)-
(C)-![]() (D)-
(D)-![]()
4.椭圆与双曲线 -y2=1有共同的焦点,一条准线的方程是x=3,则此椭圆的方程为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
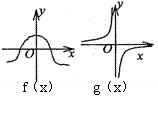
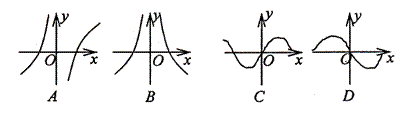
5.函数![]() 的图像如左图:则函数
的图像如左图:则函数![]() 的图像可能是
的图像可能是
 |  | ||
6.已知直线l平面α,直线m平面β,有如下四个命题:
①若αβ,则lm; ② 若α β,则lm;
③ 若lm,则αβ;④ 若lm,则αβ.其中正确的两个命题是
(A)①与② (B)①与③ (C)②与④ (D)③与④
7.等差数列{an}的前n项和为Sn,若a3+a17=10,则S19的值是
(A)55 (B)95 (C)100 (D)190
8.定义运算![]() =
=![]() . 将函数
. 将函数![]() 的图像向左平移φ(φ>0)个单位,所得图像对应的函数为偶函数,则φ的最小值为
的图像向左平移φ(φ>0)个单位,所得图像对应的函数为偶函数,则φ的最小值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9.已知向量![]() 平行,则x等于
平行,则x等于
(A)-6 (B)6 (C)-4 (D)4
10.(理)设![]() 是随机变量,且
是随机变量,且![]() ,则
,则![]() 等于 ( )
等于 ( )
(A) 0.4 (B) 4 (C) 40 (D) 400
(文)函数![]() 的值域是
的值域是
(A)R (B)[8,+![]() (C)(-∞,-3
(C)(-∞,-3![]() (D)[-3,+∞
(D)[-3,+∞![]()
11. 如果一个三位正整数的中间一个数字比另两个数字小,如305,414,879等,则称这个三位数为“凹数”,那么所有“凹数”的个数是
(A)240 (B)285 (C)729 (D)920
12、与抛物线x2=4y关于直线x+y=0对称的抛物线的焦点坐标是
(A)(1,0) (B)(![]() ,0) (C)(-1,0)
(D)(0,
,0) (C)(-1,0)
(D)(0,![]() )
)
二、填空题:本大题共4小题,每小题5分,共20分.请把答案填在答题纸题中的横线上.
13.W国参加2008奥运会有男运动员56人,女运动员42人.比赛后立即用分层抽样的方法从全体队员中抽出一个容量为28的样本进行尿样兴奋剂检查.女运动员应分别抽取 人。
14.在条件 下,函数z=-2x+y 的最大值是 。
15.若![]() 的展开式的第四项是常数项,则为
的展开式的第四项是常数项,则为![]() =
。
=
。
16.(理)设函数![]() ,则
,则![]() 是
是![]() 的导数,则
的导数,则![]() =_______。
=_______。
(文)已知正方体的表面积为18,则正方体的外接球的体积等于 。
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
乌鲁木齐市高级中学的成功同学到甲、乙、丙三所高校参加自主招生考试,各高校是否录取他相互独立。成功同学被甲、乙、丙三所高校录取的概率分别为![]() 。(假设允许成功同学可以被多所高校同时录取)
。(假设允许成功同学可以被多所高校同时录取)
(Ⅰ)求成功同学没有被录取的概率;
(Ⅱ)(理)求录取成功同学的高校数ξ的分布列和数学期望。
(文)成功同学被几个高校同时录取的可能性最大?
18.(本小题满分12分)
在锐角ABC中,设a、b、c分别为角A、B、C的对边,S为ABC的面积,且满足条件: 2sinB [
1+cos(![]() -B)] +cos2B=1+.
-B)] +cos2B=1+.
(Ⅰ)求B的度数;
(Ⅱ)若a=4,S=5,求c和b的值。
19.(本小题满分12分)
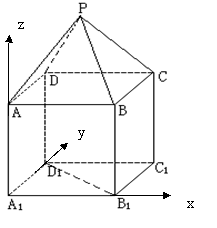
如图,P—ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2, PA=![]()
![]()
(Ⅰ)求证:PA⊥B1D1;
(Ⅱ)求平面PAD与平面BDD1B1所成的锐二面角θ的大小;
 (Ⅲ)求B1到平面PAD的距离。
(Ⅲ)求B1到平面PAD的距离。
20.(本小题满分12分)
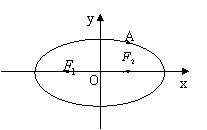
如图,设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() :
:![]() (
(![]() )的左、右焦点.设椭圆C上的点
)的左、右焦点.设椭圆C上的点![]() 到F1、F2两点距离之和等于4。
到F1、F2两点距离之和等于4。
(Ⅰ)求椭圆C的方程和离心率;
(Ⅱ)若P(x,y)是该椭圆上的一个动点,求![]() 的最大值和最小值。
的最大值和最小值。
21.(本小题满分12分)
两个二次函数![]() 与
与![]() 的图像有唯一的公共点
的图像有唯一的公共点![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)(理)设![]() ,若
,若![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的范围。并说明函数是R上的单调递增函数还是单调递减函数。
的范围。并说明函数是R上的单调递增函数还是单调递减函数。
(文)设![]() ,求
,求![]() 在x∈[-1,2]上的最大值和最小值。
在x∈[-1,2]上的最大值和最小值。
22.(本小题满分12分)
已知![]()
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)定义正数数列![]() ,证明:数列
,证明:数列 是等比数列;
是等比数列;
| |
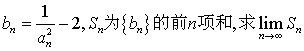 。
。
(文) 令![]() 成立的最小n值。
成立的最小n值。
参考答案
一、选择题(批改 叶素英)
1.C(文B) 2.B 3.C 4.A 5.A 6.B 7.B 8.C 9.C 10. A(文C) 11.B 12.C
二、填空题(批改 叶素英)
13. 12 14. 2 15. 21 16. (理)-3 (文)![]()
三、解答题
17(批改 林强)解:(Ⅰ)设成功同学没有被录取的概率为P0,则P0=![]() .
.![]() .
.![]() =
=![]() …4分
…4分
(Ⅱ) (文)设成功同学恰被一个高校录取的概率为P1
P1=![]() +
+![]() +
+![]() =
=![]() ……6分
……6分
设成功同学恰被两个高校录取的概率为P2
P2=![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() =
=![]() ……8分
……8分
设成功同学恰被三个高校录取的概率为P3
P3=![]() =
=![]() ……9分
……9分
∴成功同学恰被两个高校录取的可能性最大。……10分
(Ⅱ)(理)ξ可能取的值为0,1,2,3
P(ξ=0)=![]() ,P(ξ=1)=
,P(ξ=1)= ![]() , P(ξ=3)=
, P(ξ=3)=![]() ,
,
P(ξ=2)=1-![]() -
-![]() -
-![]() =
=![]() ,……7分
,……7分
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| p |
|
|
|
|
………8分
Eξ=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() ………10分
………10分
18(批改 林强)解:(Ⅰ)由已知得:2sinB·(1+sinB)+1-2sin2B=1+,………2分
化简整理,得:2sinB=,sinB=,………3分
∵三角形ABC是锐角三角形 ∴ B=60°………5分
(Ⅱ)∵ a=4,S=5,∴S= acsinB=5,∴ c=5;………8分
由b2=42+52-2·4·5·cos60°=21,得b=;………12分
19. (批改 杨帆)
解:以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系 (其他建系亦可)…2分
轴建立空间直角坐标系 (其他建系亦可)…2分
(Ⅰ)设E是BD的中点,![]() P—ABCD是正四棱锥,∴
P—ABCD是正四棱锥,∴![]()
又![]() , ∴
, ∴![]() ∴
∴![]() ………4分
………4分
∴ ![]() ∴
∴ ![]() 即
即![]() …6分
…6分
 (Ⅱ)设平面PAD的法向量是
(Ⅱ)设平面PAD的法向量是![]() ,
, ![]()
∴ ![]() 取
取![]() 得
得![]() , ………8分
, ………8分
又平面![]() 的法向量是
的法向量是![]()
∴ 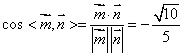 ∴
∴![]() …10分
…10分
(Ⅲ)![]()
∴![]() 到平面PAD的距离
到平面PAD的距离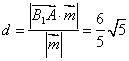 ………12分
………12分
(其他解法酌情给分)
20. (批改唐惠玲)
(Ⅰ)![]() ,
,![]() .
. ![]() ,
,![]() .…分
.…分
椭圆的方程为![]() ,………4分 因为
,………4分 因为![]() . 所以离心率
. 所以离心率![]() .………6分
.………6分
(Ⅱ)由(Ⅰ)易知![]() …………8分
…………8分
∵P(x,y),则![]() (*)
(*)
=![]() ………………10分
………………10分
![]() ,
,
∴![]() ,即点P为椭圆短轴端点时,
,即点P为椭圆短轴端点时,![]() 有最小值2;
有最小值2;
当![]() ,即点P为椭圆长轴端点时,
,即点P为椭圆长轴端点时,![]() 有最大值3 ……12分
有最大值3 ……12分
(Ⅱ)法二:还可以从(*)处用三角代换法求解
∵![]() ∴x=2sinθ,y=
∴x=2sinθ,y=![]() cosθ
cosθ
![]() =4sin2θ+3cos2θ-1=sin2θ+2………10分
=4sin2θ+3cos2θ-1=sin2θ+2………10分
∴sin2θ=0,即x=0时,![]() 有最小值2
有最小值2
sin2θ=1,即![]() 时,
时,![]() 有最大值3。………………12分
有最大值3。………………12分
21. (批改 杨华)解:(Ⅰ)由已知得 ![]() 化简得
化简得 ![]() ……………2分
……………2分
且![]() 即
即![]() 有唯一解 …3分
有唯一解 …3分
所以![]() 即
即 ![]() ……5分
……5分
消去![]() 得
得 ![]() ,解得
,解得![]() …………6分
…………6分
(Ⅱ)(理)![]() ,
,![]() ∴
∴![]()
![]()
![]() ……7分
……7分
![]() ………8分
………8分
若![]() 在
在![]() 上为单调函数,则
上为单调函数,则![]() 在
在![]() 上恒有
上恒有![]() 或
或![]() 成立。……9分
成立。……9分
因为![]() 的图象是开口向下的抛物线,所以
的图象是开口向下的抛物线,所以![]() 时
时![]() 在
在![]() 上为减函数,10分
上为减函数,10分
所以![]() ,解得
,解得 ![]() 即
即![]() 时,
时,![]() 在
在![]() 上为减函数。 12分
上为减函数。 12分
或![]() 恒成立,
恒成立,![]() =2 即
=2 即![]() 时,
时,![]() 在
在![]() 上为减函数。 12分
上为减函数。 12分
(Ⅱ)(文)由(Ⅰ)![]() ,
,![]()
∴![]()
∴![]()
![]() ∴
∴![]()
| x | -1 | (-1, 1) | 1 | (1,2) | 2 | |
|
|
| 0 |
| |||
|
| 16 | 递减 | 0 | 递增 | -2 |
令![]() =0,则x=1
=0,则x=1
列表如右
∴![]() 的最大值为16,最小值为0。
的最大值为16,最小值为0。
22. (批改 朱永红)
解:(Ⅰ)![]() 为奇函数
为奇函数
则![]() ∴
∴![]() …2分
…2分 ![]()
又![]()
![]()
![]()
![]() ………4分
………4分
(Ⅱ)![]()
![]()
![]()
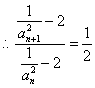 (常数)
(常数)
∴数列 是以2为首项,
是以2为首项,![]() ………8分
………8分
(Ⅲ)(理)![]() ∴ b1=2,
公比q=
∴ b1=2,
公比q=![]()
 ………10分
………10分
∴ ![]() =
=![]() =4 ………12分
=4 ………12分
(文)![]() ∴b1=2,公比q=
∴b1=2,公比q=![]()
 ………10分
又
………10分
又![]()
![]() ∴满足
∴满足![]() ………12分
………12分