【参数方程和普通方程的互化】
例1 求曲线 (
(![]() 为参数)与曲线
为参数)与曲线![]() (
(![]() 为参数)的交点.
为参数)的交点.
解:把 代入
代入![]()
得: 两式平方相加可得
两式平方相加可得![]()
∴ ![]() (
(![]() 舍去)
舍去)
于是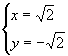 即所求二曲线的交点是(
即所求二曲线的交点是(![]() ,-
,-![]() ).
).
说明:在求由参数方程所确定的两曲线的交点时,最好由参数方程组求解,如果化为普通方程求交点时要注意等价性.如该例若化为普通方程求解时要注意点(-![]() ,
,![]() )是增解.
)是增解.
例2化直线的普通方程![]() 为参数方程(其中倾斜角
为参数方程(其中倾斜角![]() 满足
满足![]() 且
且![]() )
)
解法一:因![]() ,
,![]() ,故
,故![]()
∴ ![]()
设![]() 。取
。取![]() 为参数,则得所求参数方程
为参数,则得所求参数方程
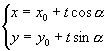
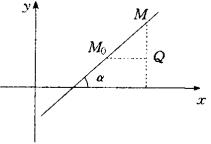 解法二:如图,
解法二:如图,![]() (
(![]() )为直线上的定点,
)为直线上的定点,![]() 为直线上的动点.因动点M与
为直线上的动点.因动点M与![]() 的数量
的数量![]() 一一对应(当M在
一一对应(当M在![]() 的向上方向或正右方时,
的向上方向或正右方时,![]() ;当M在
;当M在![]() 的下方或正左方时,
的下方或正左方时,![]() ;当M与
;当M与![]() 重合时,
重合时,![]() ),故取
),故取![]() 为参数.
为参数.
过点M作y轴的平行线,过点![]() 作
作![]() 轴的平行线,两直线相交于点Q(如图).则有
轴的平行线,两直线相交于点Q(如图).则有
![]()
![]()
∴ ![]()
![]()
即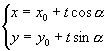 为所求的参数方程。
为所求的参数方程。
说明:①在解法二中,不必限定![]() ,
,![]() ,即不必限定
,即不必限定![]() ,
,![]() .由此可知,无论
.由此可知,无论![]() 中任意值时,所得方程都是经过
中任意值时,所得方程都是经过![]() (
(![]() ),倾斜角为
),倾斜角为![]() 的直线的参数方程.可称它是直线参数方程的“点角式”或“标准式”.
的直线的参数方程.可称它是直线参数方程的“点角式”或“标准式”.
②要充分理解解法二所示的参数![]() 的几何意义,这对解决某些问题较为方便.
的几何意义,这对解决某些问题较为方便.
③如果取![]() 为参数,则得直线参数方程
为参数,则得直线参数方程

一般地,直线的参数方程的一般形式是
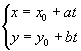 (
(![]() ,
,![]() 为参数)
为参数)
但只有当且仅当![]() ,且
,且![]() 时,这个一般式才是标准式,参数
时,这个一般式才是标准式,参数![]() 才具有上述的几何意义.
才具有上述的几何意义.
例3 求椭圆![]() 的参数方程.
的参数方程.
分析一:把![]() 与
与![]() 对比,不难发现,可设
对比,不难发现,可设![]() ,也可设
,也可设![]()
解法一:设![]() (
(![]() 为参数),则
为参数),则
![]()
∴ ![]()
故![]()
因此,所得参数方程是
(Ⅰ)![]() 或 (Ⅱ)
或 (Ⅱ)![]()
由于曲线(Ⅱ)上的点(![]() ,
,![]() ),就是曲线(Ⅰ)上的点(
),就是曲线(Ⅰ)上的点(![]() ,
,![]() ),所以曲线(Ⅱ)上的点都是曲线(Ⅰ)上的点.
),所以曲线(Ⅱ)上的点都是曲线(Ⅰ)上的点.
显然.椭圆![]() 的参数方程是
的参数方程是
![]()
分析二:借助于椭圆的辅助圆,可明确椭圆参数方程中![]() 的几何意义.
的几何意义.
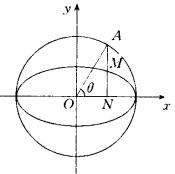 解法二:以原点O为圆心,
解法二:以原点O为圆心,![]() 为半径作圆,如图.设以
为半径作圆,如图.设以![]() 轴正半轴为始边,以动半径OA为终边的变角为
轴正半轴为始边,以动半径OA为终边的变角为![]() ,过点A作
,过点A作![]() 轴于N,交椭圆于M,取
轴于N,交椭圆于M,取![]() 为参数,则点M(
为参数,则点M(![]() )的横坐标
)的横坐标![]() (以下同解法一).
(以下同解法一).
由解法二知,参数![]() 是点M所对应的圆半径OA的转角,而不是OM的转角,因而称
是点M所对应的圆半径OA的转角,而不是OM的转角,因而称![]() 为椭圆的离角.(如果以O为圆心,
为椭圆的离角.(如果以O为圆心,![]() 为半径作圆,过M作
为半径作圆,过M作![]() ,交圆于B,由
,交圆于B,由![]() 可知
可知![]() 也是半径OB的转角).
也是半径OB的转角).
例4 用圆上任一点的半径与x轴正方向的夹角![]() 为参数,把圆
为参数,把圆![]() 化为参数方程。
化为参数方程。
分析:由圆的性质及三角函数的定义可把圆上任意一点化为![]() 的参数形式。
的参数形式。
解:如图所示,圆方程化为![]() ,设圆与x轴正半轴交于A,
,设圆与x轴正半轴交于A,![]() 为圆上任一点,过P作
为圆上任一点,过P作![]() 轴于B,OP与x轴正半轴所成角为
轴于B,OP与x轴正半轴所成角为![]() ,
,![]() ,则:
,则:
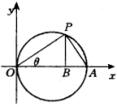
![]()
又![]() 中
中![]() ,
,
∴![]()
∴此圆的参数方程为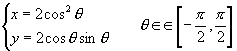
例5 设![]() (
(![]() 为参数)把普通方程
为参数)把普通方程![]() 化为以
化为以![]() 为参数的参数方程。
为参数的参数方程。
解:把![]() 代入原方程,得
代入原方程,得![]() ,
,
解得 ![]()
∴参数方程为![]() (
(![]() 为参数)
为参数)
∵![]() 与
与![]() 表示的是同一曲线,所以它们是等价的,可以省略一个。
表示的是同一曲线,所以它们是等价的,可以省略一个。
∴所求参数方程![]()
例6 化双曲线![]() 为参数方程。
为参数方程。
解:设![]() ,代入
,代入![]() 为,得
为,得![]()
∴![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() )
)
这是同学中较为常见的解法,这种解法是错误的,那么错在哪里呢?请你找出来。
错误在于,双曲线![]() 上x的取值范围是不等于零的一切实数,错解中得到的参数方程中x的取值范围仅仅
上x的取值范围是不等于零的一切实数,错解中得到的参数方程中x的取值范围仅仅![]() ,故错解中得到的参数方程只表示双曲线
,故错解中得到的参数方程只表示双曲线![]() 上一部分,不符合普通方程与参数方程的等价性要求,普通方程化为参数方程时关键是选择适当的参数,注意使所得参数方程与原普通方程中变量x、y的允许值范围要保持一致。
上一部分,不符合普通方程与参数方程的等价性要求,普通方程化为参数方程时关键是选择适当的参数,注意使所得参数方程与原普通方程中变量x、y的允许值范围要保持一致。
下面给出正确解法:设![]() ,代入
,代入![]() 得
得![]() 。
。
∴![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数,
为参数,![]() )
)
例7 化参数方程
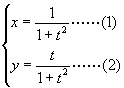 (
(![]() 为参数)为普通方程。
为参数)为普通方程。
分析一:用代入消元法,从已知方程中解出参数![]() ,代入后消去参数。
,代入后消去参数。
解法一:∵![]()
∴ 即
即![]()
将它代入(1),并化简得
![]() (
(![]() )
)
分析二:用整体消参法。注意![]() 表达式的分母相同,而分子的平方和恰为原来相同的分母。
表达式的分母相同,而分子的平方和恰为原来相同的分母。
解法二:![]() 得
得
![]()
又∵![]() ∴
∴ ![]()
于是得所求普通方程为![]()
即![]()
分析三:因为![]() ,所以
,所以![]() 。从
。从![]() 表达式可联想万能公式。于是可用三角变换,然后利用三角公式再消参。
表达式可联想万能公式。于是可用三角变换,然后利用三角公式再消参。
解法三:∵![]() ,
,
∴ 可令![]() (
(![]() ,
,![]() )
)
又∵![]()
于是得
![]() 得
得 ![]()
即![]()
∵![]() ,(
,(![]() )
)
∴![]() (
(![]() )
)
即![]() ,∴
,∴![]()
∴普通方程是![]() (
(![]() )
)
说明:解法一是用代入法消参,解法二是整体消参法,解法三是运用万能公式,三角变换消参,三种解法中都应注意![]() 的限制条件,使参数方程化为普通方程时保持等价性。
的限制条件,使参数方程化为普通方程时保持等价性。
例8将下列参数方程(其中![]() ,
,![]() 为参数)化为普通方程。
为参数)化为普通方程。
(1)![]() (2)
(2)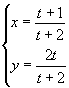 (3)
(3)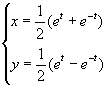
解:(1)∵
∴ ![]() (
(![]() )为所求。
)为所求。
(2)由![]() ,得
,得![]() (
(![]() )
)
将它代入![]() ,并化简得
,并化简得![]() (
(![]() )
)
另解:∵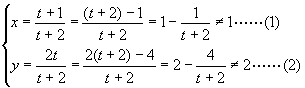
![]() 并整理得
并整理得
![]() (
(![]() )
)
(3)∵![]()
且![]()
∴所求普通方程为![]()
说明:(1)小题是用三角公式变形后用代入法消参,(2)是用代入(消元)法消参变形后整体消参,(3)小题是通过代数变换法消参。但都应特别注意等价性。
例9 对于方程![]() (a,b为常数)
(a,b为常数)
(1)当t为常数,![]() 为参数时,方程表示何种曲线;
为参数时,方程表示何种曲线;
(2)当t为参数,![]() 为常数时,方程表示何种曲线
为常数时,方程表示何种曲线
解:(1)当t为常数,原方程可变形为
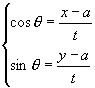 两式平方相加得
两式平方相加得![]()
即![]()
这是以(a,b)为圆心,![]() 为半径的圆。
为半径的圆。
(2)当![]() 为常数时,
为常数时,
由第一式得![]() 代入第二式得
代入第二式得![]()
即![]()
这是过点(a,b),斜率为![]() 的一条直线
的一条直线
小结:同一参数方程,由于参数不同,所表示的曲线也不同,消去参数化为普通方程后,曲线的类型也就显现出来。
例10 已知直线![]() 过点P(2,0),斜率为
过点P(2,0),斜率为![]() 。直线
。直线![]() 和抛物线
和抛物线![]() 相交于A、B两点,线段AB的中点为M。求:
相交于A、B两点,线段AB的中点为M。求:
(1)线段PM的长![]() ;
;
(2)M点的坐标;
(3)线段AB的长![]()
解:如图。
(1)由直线![]() 过点P(2,0),斜率为
过点P(2,0),斜率为![]() 。设其倾斜角为
。设其倾斜角为![]() ,则有
,则有
![]()
可得直线![]() 的标准参数方程为:
的标准参数方程为:
 (其中
(其中![]() 为参数)
为参数)
设直线![]() 上两点A、B分别对应参数
上两点A、B分别对应参数![]() 、
、![]() ,
,
由方程组: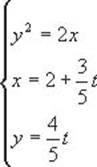
消去![]() 可得:
可得:![]()
有 ![]() ,
,![]()
由M为AB的中点,
∴ ![]()
(2)设M点对应参数为![]() ,则有
,则有
![]()
∴ M点坐标为:

∴M点坐标为(![]() ,
,![]() )
)
(3)由![]()
分别代入![]() ,
,![]()
可得 ![]()
点拨:利用直线的标准参数方程中参数![]() 的几何含义,在解决诸如直线
的几何含义,在解决诸如直线![]() 上的两点距离、某两点的中点以及与此相关的一些问题时,显得很方便和简捷。
上的两点距离、某两点的中点以及与此相关的一些问题时,显得很方便和简捷。
例11 已知椭圆![]() 上的一个点P(
上的一个点P(![]() ),求
),求![]() 的最值。
的最值。
解:设椭圆![]() 的参数方程为:
的参数方程为:
![]() (
(![]() 为参数,
为参数,![]() )
)
∴![]()
![]()
![]() ,(其中
,(其中![]() )
)
∵ ![]()
∴ ![]()
即![]() 的最大值是
的最大值是![]() ,最小值是-
,最小值是-![]() 。
。
点拨:这个题虽然很简单,但它说明了一个道理:曲线的参数方程不仅表示了曲线,同时也表示了曲线上的点的坐标.当曲线的参数方程表示曲线上的点的坐标时,实际上起到了消元的作用,即用一个参数表示了![]() 、
、![]() ,因此,在求某些几何量的最值时,参数方程可以起到一元化即消元的作用.
,因此,在求某些几何量的最值时,参数方程可以起到一元化即消元的作用.
例12 过点M(2,1)作曲线![]() (
(![]() 为参数)的弦AB,若M为AB的三等分点,求AB直线方程。
为参数)的弦AB,若M为AB的三等分点,求AB直线方程。
解:设AB的方程为![]() (t为参数),将x,y代入曲线
(t为参数),将x,y代入曲线![]() (
(![]() 为参数)即
为参数)即![]() ,
,
整理、化简得![]() ,
,
![]() ①
①
![]() ②
②
∵点M在AB的内部 ∴![]()
∴![]() 。
。
将①、②代入上式有![]() 。
。
解得![]() ,
,
则AB的方程为![]()
小结:本题是首先设出过定点的参数方程,然后和椭圆方程联立,再利用韦达定理及直线参数方程中t的意义,求得斜率,用点斜式写出直线方程。
例13 圆O内一定点A,过A任作两互相垂直的弦,求证这两弦长的平方和为定值。
证明:以圆心O为原点,OA所在的直线为x轴建立直角坐标系,
设圆的方程![]() ,过定点
,过定点![]() 互相垂直的两弦PQ、RS的方程分别为
互相垂直的两弦PQ、RS的方程分别为 即
即
分别代入圆方程,得![]() ,其二根为
,其二根为![]() 、
、![]() ,
,
![]() ,其二根为
,其二根为![]() 、
、![]() ,故有
,故有

∴两弦平方和为定值![]()
小结:涉及圆的弦长问题,可利用直线参数方程来解。
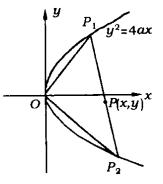 例14 已知
例14 已知![]() 是抛物线
是抛物线![]() 的一动弦,O为原点。当
的一动弦,O为原点。当![]() 恒为直角时,如图求弦
恒为直角时,如图求弦![]() 的中点P的轨迹方程。
的中点P的轨迹方程。
分析 点P是![]() 的中点,点P的坐标
的中点,点P的坐标![]() 与
与![]() ,
,![]() 的坐标
的坐标![]() ,
,![]() ,
,![]() 、
、![]() 相关,如果选取
相关,如果选取![]() ,
,![]() ,
,![]() 、
、![]() 作为参数,则要列出
作为参数,则要列出![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 有关的五个方程,最后消去参数
有关的五个方程,最后消去参数![]() ,
,![]() ,
,![]() 、
、![]() 就可以得到P点的轨迹方程。
就可以得到P点的轨迹方程。
解 设P(![]() ),
),![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() )
)
∵P是![]() 的中点
的中点
∴![]() ①
①
![]() ②
②
∵![]() ,
,![]() 在抛物
在抛物![]() 上
上
∴![]() ③
③
![]() ④
④
又∵![]() 恒为直角,即
恒为直角,即![]()
∴![]() ⑤
⑤
由③×④:![]()
∴![]()
由③+④:![]()
∴![]()
把①、②式代入得:![]()
∴ P点的轨迹方程是![]()
说明 此题的解法是利用参数求点的轨迹方程,参数的个数可以是一个,也可以是几个,所列出的参数与点的坐标![]() 之间的方程的个数要比参数个数多一个,最后消去参数,得出轨迹方程.解决这类问题的关键是如何选取参数.此题还有一种选取参数的方法.
之间的方程的个数要比参数个数多一个,最后消去参数,得出轨迹方程.解决这类问题的关键是如何选取参数.此题还有一种选取参数的方法.
设直线![]() 的斜率为
的斜率为![]() ,根据
,根据![]()
则![]() 的方程是
的方程是![]() ,
,
![]() 的方程是
的方程是![]() 。
。
由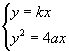 解得
解得![]()
由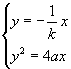 解得
解得![]()
设![]() ,根据P是
,根据P是![]() 的中点
的中点
∴![]() (1)
(1)
![]() (2)
(2)
由![]()
把(1)代入:![]()
∴P点的轨迹方程是:![]()