高考数学试题精选(一)
卞志业 2008-1-17
1.(0712广东深圳)设![]() 是方程
是方程![]() 的解,则
的解,则![]() 属于区间
( )
属于区间
( )
A. (0,1) B. (1,2) C. (2,3) D.(3,4)
2. (0712广东深圳)过原点与曲线![]() 相切的直线方程是
相切的直线方程是
A.![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
3(理). (0712广东深圳)4张软盘与5张光盘的价格之和不小于20元,而6张软盘与3张光盘的价格之和不大于24元,则买3张软盘与9张光盘至少需要 ( )
A.15元 B.22元 C.36元 D.72元
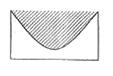 3.(0712山东青岛)右图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影、部分的面积约
( )
3.(0712山东青岛)右图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影、部分的面积约
( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
4(理).(0712广东深圳)若![]() 的展开式中的第五项等于
的展开式中的第五项等于![]() ,则
,则![]() ( )
( )
A.1
B.![]() C.2
D.4
C.2
D.4
4. (0712广东深圳)下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量a的性质a2=a2类比得到复数z的性质z2=z2;
③方程![]() 有两个不同实数根的条件是
有两个不同实数根的条件是![]() 可以类比得到:方程
可以类比得到:方程![]() 有两个不同复数根的条件是
有两个不同复数根的条件是![]() ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义.
其中类比错误的是 ( )
A.①③ B. ②④ C. ①④ D. ②③
5.(0712广东深圳)已知![]() ,
,![]() ,曲线
,曲线![]() 上一点P到F(3,0)的距离为6,Q为PF的中点,O为坐标原点,则OQ= ( )
上一点P到F(3,0)的距离为6,Q为PF的中点,O为坐标原点,则OQ= ( )
A.1 B.5 C.1或5 D. 4
6.(0712广东深圳)抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,且与抛物线有公共点,
,且与抛物线有公共点,
则直线![]() 的倾斜角的取值范围是
( ) A.
的倾斜角的取值范围是
( ) A.![]() B.
B.![]()
C.![]() D.
D.![]()
 7. (0712广东深圳)定义
7. (0712广东深圳)定义![]() 的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是
的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是
(1) (2) (3) (4) (A) (B)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(0712广东深圳)正三棱锥底面边长为a,侧棱与底面成角为![]() ,过底面一边作一截面使其与底面成
,过底面一边作一截面使其与底面成![]() 的二面角,则此截面的面积为( )
的二面角,则此截面的面积为( )
A.![]() B.
B.![]() C .
C .![]() D.
D.![]()
9.(0712广东深圳)对于![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是(
)
的取值范围是(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.(0712山东潍坊)一化工厂明年一月起,若不改善生产环境按现状生产,每月收入72万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月增加2万元. 如果明年一月投资600万元增加废物回收净化设备(改造设备时间不计),一方面可以改善环境,另一方面也可以大大降低原料成本,据测算设备投产后每月收入为150万元,同时该厂不仅不受处罚而且能得到环保部门一次性100万元的奖励,则投资后(从一月算起)第( )个月开始见效(即投资改造后的纯收入大于不改造时的纯收入)? ( )
A.4 B.5 C.6 D.7
11.(0801福建福州)设![]() 的平均数,m是
的平均数,m是![]() 的平均数,n是
的平均数,n是![]() 的平均数,则下列各式正确的是 ( )
的平均数,则下列各式正确的是 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.(0712甘肃张掖)为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文![]() 对应密文
对应密文![]() ,例如,明文
,例如,明文![]() 对应密文
对应密文![]() .当接收方收到密文
.当接收方收到密文![]() 时,则解密得到的明文为 ( )
时,则解密得到的明文为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13(理). (0712广东深圳)函数 的图象与x轴所围成的封闭图形的面积等于 .
的图象与x轴所围成的封闭图形的面积等于 .
 13. (0712广东深圳)一个算法的程序框图如右图所示,若该程序输出的结果为
13. (0712广东深圳)一个算法的程序框图如右图所示,若该程序输出的结果为![]() ,则判断框中应填入的条件是
.
,则判断框中应填入的条件是
.
14(理). (0712广东深圳)若![]() ,则
,则![]() .
.
14.(0712甘肃张掖)函数![]() 是定义在R上的奇函数,给出下列命题:①
是定义在R上的奇函数,给出下列命题:①![]() =0, ②若
=0, ②若![]() 在
在![]() 上有最小值为-1,则
上有最小值为-1,则![]() 在
在![]() 上有最大值1;③若
上有最大值1;③若![]() 在
在![]() 上为增函数,则
上为增函数,则![]() 在
在![]() 上为减函数;④若x>0,
上为减函数;④若x>0,![]() =x2-2x;则x<0时,
=x2-2x;则x<0时,![]() =-x2-2x.
=-x2-2x.
其中所有正确的命题序号是______________ .
15(理).(0712广东深圳)某工程队有6项工程需要先后单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后才能进行,又工程丁必须在工程丙完成后立即进行,那么安排这6项工程的不同的排法种数是 .(用数字作答)
15.(0712安徽蚌埠)一只蚂蚁在边长分别为3,4,5的三角形的边上爬行,某时刻该蚂蚁距离三角形的三个顶点的距离均超过1的概率是_______。
16.(0712山东实验)在数列中,已知![]() ,这个数列的通项公式是
,这个数列的通项公式是![]() =
。
=
。
17. (0712甘肃张掖)
设函数![]()
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,的对边,![]()
求b,c的长.
18. (0712广东深圳)一个几何体的三视图如右图所示,其中正视图和侧视
图是腰长为6的两个全等的等腰直角三角形.
(Ⅰ)请画出该几何体的直观图,并求出它的体积;
 (Ⅱ)用多少个这样的几何体可以拼成一个棱长为
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为
6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1
的棱CC1的中点为E, 求平面AB1E与平面ABC所成锐二面
角的余弦值.
19.(理科)(0712广东深圳)高校招生是根据考生所填报的志愿,从考试成绩所达到的最高第一志愿开始,按顺序分批录取,若前一志愿不能录取,则依次给下一个志愿(同批或下一批)录取.某考生填报了三批共6个不同志愿(每批2个),并对各志愿的单独录取以及能考上各批分数线的概率进行预测,结果如“表一”所示(表中的数据为相应的概率,a、b分别为第一、第二志愿).
(Ⅰ)求该考生能被第2批b志愿录取的概率;
| 批次 | 高考上线 | a | b |
| 第1批 | 0.6 | 0.8 | 0.4 |
| 第2批 | 0.8 | 0.9 | 0.5 |
| 第3批 | 0.9 | 0.95 | 0.8 |
(Ⅱ)求该考生能被录取的概率;
(Ⅲ)如果已知该考生高考成绩已达到第2批分数线却未能达到第1批分数线,请计算其最有可能在哪个志愿被录取?
(以上结果均保留二个有效数字)
19.从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件![]() :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率![]() .
.
(1)求从该批产品中任取1件是二等品的概率![]() ;
;
(2)若该批产品共100件,从中任意抽取2件,求事件![]() :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率![]() .
.
20. (0712广东深圳)定义在D上的函数![]() ,如果满足:
,如果满足:![]() ,
,![]() 常数
常数![]() ,都有
,都有![]() ≤M成立,则称
≤M成立,则称![]() 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
(Ⅰ)试判断函数![]() 在[1,3]上是不是有界函数?请给出证明;
在[1,3]上是不是有界函数?请给出证明;
(Ⅱ)若已知质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
21. (0712广东深圳)双曲线M的中心在原点,并以椭圆![]() 的焦点为焦点,以抛物线
的焦点为焦点,以抛物线![]() 的准线为右准线.
的准线为右准线.
(Ⅰ)求双曲线M的方程;
(Ⅱ)设直线![]() :
:![]() 与双曲线M相交于A、B两点,O是原点.
与双曲线M相交于A、B两点,O是原点.
① 当![]() 为何值时,使得
为何值时,使得![]()
![]()
![]()
![]() ?
?
② 是否存在这样的实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称?若存在,求出
对称?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
22.(0712广东深圳)已知数列![]() 满足
满足![]() ,
,![]()
(1)设![]() ,求证数列
,求证数列![]() 是等差数列,并写出其通项公式;
是等差数列,并写出其通项公式;
(2)在(1)的条件下,数列![]() ,
,![]() 满足
满足![]() ,且对于任意正整数
,且对于任意正整数![]() ,不等式
,不等式 ![]() 恒成立,求正数
恒成立,求正数![]() 的取值范围.
的取值范围.
高考数学试题精选(一)答案
一、选择题:本大题主要考查基本知识和基本运算 共12小题,每小题5分,满分60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | C | C | B A | C D | C | B | B | D | C | C | C | C |
二、填空题: 本大题主要考查基本知识和基本运算. 本大题共4小题,每小题4分,满分16分。
13. 5/6 (无) 14. 0 ①②④ _
15. 1800
1/2
16.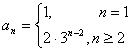
三、解答题: 本大题共6小题,其中17~21题每题12分,22题14分,满分74分.解答应写出文字说明、演算步骤或推证过程.
17.解(Ⅰ)![]()
![]()
![]() ……………………(3分)
……………………(3分)
∴![]() …………………(5分)
…………………(5分)
(Ⅱ)f
(A) =
2 即![]() …………………(7分)
…………………(7分)
![]()
∴b2 + c2-bc = 3 ①
又b2 + c2 + 2bc = 9 ②
②-① bc = 2 ③
b + c = 3 ④
b > c ⑤
 由③,④解出
由③,④解出![]() ……………………(10分)
……………………(10分)
18.
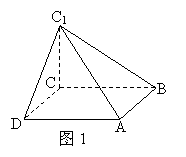
解:(Ⅰ)该几何体的直观图如图1所示,它是有一条
侧棱垂直于底面的四棱锥. 其中底面ABCD是边长为6的
正方形,高为CC1=6,故所求体积是
![]() ------------------------4分
------------------------4分
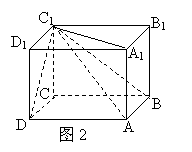
(Ⅱ)依题意,正方体的体积是原四棱锥体积的3倍,
故用3个这样的四棱锥可以拼成一个棱长为6的正方体,
其拼法如图2所示. ------------------------6分
证明:∵面ABCD、面ABB1A1、面AA1D1D为全等的
正方形,于是
![]() 故所拼图形成立.---8分
故所拼图形成立.---8分
(Ⅲ)方法一:设B1E,BC的延长线交于点G,
连结GA,在底面ABC内作BH⊥AG,垂足为H,
连结HB1,则B1H⊥AG,故∠B1HB为平面AB1E与
平面ABC所成二面角或其补角的平面角. --------10分
在Rt△ABG中,![]() ,则
,则

![]() ,
,![]() ,
,
![]() ,故平面AB1E与平面ABC所成二面角的余弦值为
,故平面AB1E与平面ABC所成二面角的余弦值为![]() .---14分
.---14分
方法二:以C为原点,CD、CB、CC1所在直线分别为x、y、z轴建立直角坐标系(如图3),∵正方体棱长为6,则E(0,0,3),B1(0,6,6),A(6,6,0).
设向量n=(x,y,z),满足n⊥![]() ,n⊥
,n⊥![]() ,
,
于是![]() ,解得
,解得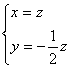 .
--------------------12分
.
--------------------12分
取z=2,得n=(2,-1,2). 又![]() (0,0,6),
(0,0,6),
故平面AB1E与平面ABC所成二面角的余弦值为![]() .
----------------14分
.
----------------14分
19. 解:分别记该考生考上第1、2、3批分数线为事件A、B、C,被相应志愿录取为事件Ai、Bi、Ci,(i=a、b), 则以上各事件相互独立. -------------------------------------2分
(Ⅰ)“该考生被第2批b志愿录取”包括上第1批分数线和仅上第2批分数线两种情况,故所求概率为
![]()
![]()
![]() . -----------------------------------------------------------------------------------6分
. -----------------------------------------------------------------------------------6分
(Ⅱ)设该考生所报志愿均未录取的概率为![]() ,则
,则
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
∴该考生能被录取的概率为![]() . ------------10分
. ------------10分
|
| 批次 | a | b |
| 第2批 | 0.9 | 0.05 |
| 第3批 | 0.048 | 0.0020 |
从表中可以看出,该考生被第2批a志愿录取的概率最大,故最有可能在第2批a志愿被录取. ------14分
20.(本小题满分14分)
解:(Ⅰ)∵![]() ,当
,当![]() 时,
时,![]() .
.
∴![]() 在[1,3]上是增函数.---------------------------------3分
在[1,3]上是增函数.---------------------------------3分
∴当![]() 时,
时,![]() ≤
≤![]() ≤
≤![]() ,即 -2≤
,即 -2≤![]() ≤26.
≤26.
∴存在常数M=26,使得![]() ,都有
,都有![]() ≤M成立.
≤M成立.
故函数![]() 是[1,3]上的有界函数.---------------------------6分
是[1,3]上的有界函数.---------------------------6分
(Ⅱ)∵![]() . 由
. 由![]() ≤1,得
≤1,得![]() ≤1
≤1
∴
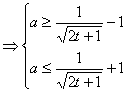
令![]() ,则
,则![]() .
.
当![]() 时,有
时,有![]() ,
,
∴![]() 在[0,+∞
在[0,+∞![]() 上单调递减.
-------------------------------10分
上单调递减.
-------------------------------10分
故当t=0 时,有![]() ;
;
又![]() ,当t→+∞时,
,当t→+∞时,![]() →0,
→0,
∴ ![]() ,从而有
,从而有![]() ≤0,且
≤0,且![]() . ∴0≤a≤1;
故所求a的取值范围为0≤a≤1.---------------------------------------------14分
. ∴0≤a≤1;
故所求a的取值范围为0≤a≤1.---------------------------------------------14分
21.(本小题满分14分)
解:(Ⅰ)易知,椭圆![]() 的半焦距为:
的半焦距为:![]() ,
,
又抛物线![]() 的准线为:
的准线为:![]() .
.
设双曲线M的方程为![]() ,依题意有
,依题意有![]() ,
,
故![]() ,又
,又![]() .
.
∴双曲线M的方程为![]() . ------------------------4分
. ------------------------4分
(Ⅱ)设直线![]() 与双曲线M的交点为
与双曲线M的交点为![]() 、
、![]() 两点
两点
联立方程组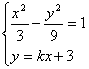 消去y得
消去y得
![]() ,
,
∵![]() 、
、![]() 两点的横坐标是上述方程的两个不同实根,
∴
两点的横坐标是上述方程的两个不同实根,
∴![]()
∴![]()
![]() ,从而有
,从而有
![]() ,
,![]() .
.
又![]() ,
,![]()
∴![]() .
.
① 若![]()
![]()
![]()
![]() ,则有
,则有 ![]() ,即
,即![]()
![]() .
.
∴当![]() 时,使得
时,使得![]()
![]()
![]()
![]() . -----------------------------8分
. -----------------------------8分
② 若存在实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称,则必有
对称,则必有 ![]() ,
,
因此,当m=0时,不存在满足条件的k;------------------------------------10分
当![]() 时,由
时,由 得
得 ![]()
![]()
![]()
![]()
∵A、B中点![]() 在直线
在直线![]() 上,
上,
∴![]() 代入上式得
代入上式得
![]()
![]() ;又
;又![]() , ∴
, ∴![]()
将![]() 代入并注意到
代入并注意到![]() ,得
,得 ![]() .
.
∴当![]() 时,存在实数
时,存在实数![]() ,使A、B两点关于直线
,使A、B两点关于直线![]() 对称.
对称.
22.解:(1)证明:由![]() 得
得![]() ,
,
因![]() ,所以
,所以![]()
又![]() ,
,![]()
![]() 是以1为首项,2为公差的等差数列,其通项公式为
是以1为首项,2为公差的等差数列,其通项公式为![]()
(2)由题意,即![]() 对任意正整数
对任意正整数![]() 恒成立,记
恒成立,记 ![]()
![]() ,
,
则![]()
 ,
,
所以![]() ,即
,即![]() 单调递增,故
单调递增,故![]()
所以![]()