08高考数学第七次月考模拟卷

08高考数学第七次月考模拟卷

数学试题（文科）

一、选择题（本大题共10小题，每小题5分典50分。在每小题给出的四个选项中，只有一项是符合题目要求的。）

1．直线的倾斜角大小为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．30°　　　　　　　　　 B．60°　　　　　　　　　 C．120°　　　　　　　　 D．150°

2．设集合，若，则实数可取不同值的个数是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

A．2　　　　　　　　　　　　B．3　　　　　　　　　　　　C．4　　　　　　　　　　　　D．5

3．已知，且，则向量与向量的夹角是　　　　　　　　　　 （　　）

A．30°　　　　　　　　　 B．45°　　　　　　　　　 C．90°　　　　　　　　　 D．135°

4．椭圆的一个焦点是（0，2），那么的值为　　　　　　　　　　　　　　　　 （　　）

A．　　　　　　　　　　B．　　　　　　　　　C．1　　　　　　　　　　　　D．

5．二项式的展开式中，常数项为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．30　　　　　　　　　　　B．48　　　　　　　　　　　 C．60　　　　　　　　　　　D．120

6．已知是等差数列的前项和，且，则的值为　　　　　　　 （　　）

A．117　　　　　　　　　　 B．118　　　　　　　　　　 C．119　　　　　　　　　　 D．120

7．在平面直角坐标系中，不等式组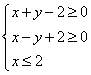表示的平面区域的面积等于　　　 （　　）

　　　 A．1　　　 　　　　 B．2　　　　　 　　 C．3　　　　　 　　 D．4

8．从5位男生和4位女生中选取3人担任年级学生会干部中的三个不同职务，其中一个职务必须由女生担任，则不同的可能情形种数为　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．674　　　　  　 B．224　　　　  　 C．324　　　　　 D．464

9．已知直线，直线，则下列四个命题：①∥；

②　　 ∥；③∥；④∥。其中正确的是（　　）

A．①②　　　　　　　　　 B．③④　　　　　　　　　 C．②④　　　　　　　　　 D．①③

1,3,5

10．已知函数的图象与函数的图角的交点为，，则有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　　　　　B．　　　　　　 C．　　　　　　D．

二、填空题（本大题共5小题，每小题5分，共25分，把答案填写在答卷上。）

11．已知A，B，C是△ABC的三个内角，则的最大值为　　　　　  。

12．已知正三棱柱ABC—A₁B₁C₁的侧棱长与底面边长相等，则AB₁与侧面ACC₁A₁所成角的正弦值等于　　　　　  。

13．圆上的点处的切线方程为　　　　　　　  。

14．函数的单调递增区间为　　　　　　　　 。若将函数的图像向左平移个单位，得到的图像关于原点对称，则的最小值为　　　　　　 。

15．对于函数，给出下列命题：①当时，在定义域上为单调增函数；②的图象的对称中心为；③对任意，都不是奇函数；④当时，为偶函数；⑤当时，对于满足条件的所有，总有。其中正确命题的序号为　　　　　  。

三、解答题（本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。）

16．（本题满分12分）

　　已知

　 （1）若，求的最小正周期；

　 （2）若对任意时，恒成立，求的取值范围。

17．（本小题满分12分）

如图所示，直三棱柱ABC—A₁B₁C₁中，AC=BC=1，

∠ACB=90°，点D为AB的中点。

　 （1）求证：BC₁ ∥面A₁DC；

　 （2）若，求二面角A₁—CD—A的平面角的大小。

18．（本小题满分12分）

某大型体育网站对2008年北京奥运会部分体育竞技项目进行预测，其中进入女子羽毛球团体决赛的队伍可能是中国女羽与印尼女羽，由于奥运会女羽冠军争夺是以“五局三胜”制进行，根据以往战况，中国女羽每一局赢的概率为，倘若在比赛中，第一局印尼女羽先胜一局，在这个条件下：

　 （1）求中国女羽取胜的概率（用分数作答）；

　 （2）设决赛中比赛总的局数，求的分布列及（用分数作答）。

19．（本小题满分13分）

在数列中，已知，

且

　 （1）求证：数列为等比数列；

　 （2）求数列的通项公式；

　 （3）求最大的正整数，使得数列前项和满足。

20．（本题满13分）

如图所示，曲线OMB是函数的图象，BA⊥轴于A（6，0），曲线段OMB上一点处的切线PQ交轴于P，交线段AB于Q。

　 （1）试用表示切线PQ的方程；

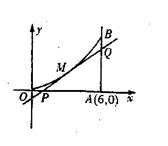　 （2）试用表示出△QAP的面积；若函数在上单调递减，试求出的最小值。

21．（本小题满分13分）

设抛物线C：过点，其准线为，焦点为F。

　 （1）求抛物线C的方程；

　 （2）若准线与轴的交点为M，AB是经过焦点F的抛物线的任意弦，记为MA的斜率，为MB的斜率，求的值；

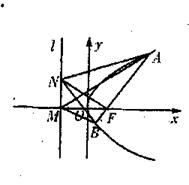　 （3）试探究：对于抛物线的准线上的任意一点N，经过焦点F的抛物线的任意弦AB，记为NA的斜率，为NB的斜率，为NF的斜率，是否有、、成等差数列，请说明理由。

参考答案

一、选择题

1．D　 2．B　 3．B　 4．C　 5．C　 6．C　 7．D　 8．B　 9．D　 10．D

1,3,5

二、填空题

11．　 12．　 13．　

14．；　 15．②③⑤

三、解答题

16．解：（1）由已知，有

　 （2）依题意得：

17．解：（1）连接AC₁与A₁C交于点E，则E为AC₁的中点，又点D是AB中点，则DE//BC₁，而DE面A₁DC，BC₁面A₁DC，则有BC₁//面A₁DC；

　 （2）因为CD⊥AB，CD⊥AA₁，则CD⊥面ADA₁，

所以CD⊥A₁D，则∠A₁DA为二面角A₁—CD—A的平面角，

又AA₁==AD，故∠A₁DA=45°，

即二面A₁—CD—A的平面角大小为45°。

18．解：（1）中国女羽取胜的情况有两种：

①中国女羽连胜三局

②中国女羽在第2局到第4局中赢两局，且第5局赢

故中国女羽取胜的概率为

故所求概率为；

　 （2）比赛局数：

的分布列为：

	3	4	5
P

19．解：（1）证明：由

则为等比数列；

　 （2）由（1）知

　 （3）由（2）知，

将其代入不等式

20．解析：（1）设点，

　 （2）由（1）可求得，

　　

21．解：（1）由H（3，—6）在抛物线C上得：，则抛物线C的方程为；

　 （2）因为点F（3，0），设直线AB的方程为：。

　　（3）因为点F（3，0），设直线AB的方程为：，

　　故k₁、k、k₂成等差数列。