高考理科数学模拟示范卷(一)
数学(理科,江西专用)
江西金太阳教育研究所数学研究室 编
一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)
1.数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,数列
的等差数列,数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.若
的等差数列.若![]() ,则
,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 的最小正周期为( ).
的最小正周期为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,则
,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.两个集合![]() 与
与![]() 之差记为“
之差记为“![]() ”,定义为
”,定义为![]() .如果集合
.如果集合
![]() ,集合
,集合![]() ,那么
,那么![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设![]() ,
,![]() ,则
,则![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.
C. ![]() 或
或![]() D.不存在
D.不存在
6.已知球面上的四点![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 的长分别为
的长分别为![]() 、
、![]() 、
、![]() ,且这三条线段两两 垂直,则这个球面的表面积为( ).
,且这三条线段两两 垂直,则这个球面的表面积为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.正方体![]() 中,若
中,若![]() 为棱
为棱![]() 的中点,则直线
的中点,则直线![]() 与平面
与平面![]() 所成角的正切值为( ).
所成角的正切值为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知椭圆![]() 的两焦点分别为
的两焦点分别为![]() 、
、![]() ,点
,点![]() 满足
满足![]() ,则
,则![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,若满足
两点,若满足![]() ,则
,则![]() (
(![]() 为坐标原点)等于( ).
为坐标原点)等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知方程![]() 的两根为
的两根为![]() ,且
,且![]() ,则
,则![]() 的取值范围是( ).
的取值范围是( ).
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.五个人站在图中![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个位置上互相传球,规定每次
五个位置上互相传球,规定每次
只能传给相邻的人,如![]() 不能直接传给
不能直接传给![]() 等.若开始时球在
等.若开始时球在![]() 手中,则经
手中,则经
过四次传球后,球又回到![]() 手中的传法种数是( ).
手中的传法种数是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.设![]() 为整数
为整数![]() (十进制)的各位数上的数字的平方之和,比如
(十进制)的各位数上的数字的平方之和,比如![]() ,
,
记![]() ,
,![]() ,则
,则![]() 等于( ).
等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第(Ⅱ)卷 (非选择题 共90分)
二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.已知![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]()
![]() .
.
14.已知![]() ,且
,且![]() ,那么二项式
,那么二项式![]() 的展开式中常数项为
的展开式中常数项为![]() .
.
15.过双曲线![]() :
:![]() 的左顶点
的左顶点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,若
,若![]() 与双曲线
与双曲线![]() 的两条渐近线分别交于点
的两条渐近线分别交于点![]() 、
、![]() ,且
,且![]() ,则双曲线
,则双曲线![]() 的离心率
的离心率![]() .
.
16.在![]() 这
这![]() 个连号中抽奖,若抽出的号码中,出现仅出现两个偶数数字则中奖,那么抽取一个号码能中奖的概率是
个连号中抽奖,若抽出的号码中,出现仅出现两个偶数数字则中奖,那么抽取一个号码能中奖的概率是![]() .
.
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,且
,且![]() 、
、 ![]() 、
、![]() 成等比数列.
成等比数列.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
18.(本小题满分12分)四个纪念币![]() 、
、![]() 、
、![]() 、
、![]() ,投掷时正面向上的概率如下表所示
,投掷时正面向上的概率如下表所示![]() .
.
| 纪念币 |
|
|
|
|
| 概率 |
|
|
|
|
这四个纪念币同时投掷一次,设![]() 表示出现正面向上的个数.
表示出现正面向上的个数.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在概率![]() 中,若
中,若![]() 的值最大,求
的值最大,求![]() 的取值范围;
的取值范围;
19.(本小题满分12分)如图,在斜三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() 与底面
与底面![]() 成
成![]() 的角,
的角,![]() .底面
.底面![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,
 其重心为
其重心为![]() 点.
点.![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() .
.
(Ⅰ)求证:![]() 侧面
侧面![]() ;
;
(Ⅱ)求平面![]() 与底面
与底面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
20.(本小题满分12分)设![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求证:当![]() 时,
时,![]() 对任意正实数
对任意正实数![]() 成立.
成立.
21.(本小题满分12分)已知为正实数,数列![]() 由
由![]() ,
,![]() 确定.
确定.
(Ⅰ)对于一切的![]() ,证明:
,证明:![]() ;
;
(Ⅱ)若![]() 是满足
是满足![]() 的正实数,且
的正实数,且![]() ,证明:
,证明:![]() .
.
22.(本小题满分14分)已知常数列![]() ,点
,点![]() 是直角
是直角![]() 的直角顶点,顶点
的直角顶点,顶点![]() 在定直线
在定直线![]() :
:![]() 上移动,斜边
上移动,斜边![]() 所在直线恒过定点
所在直线恒过定点![]() .
.
(Ⅰ)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设![]() 是轨迹
是轨迹![]() 上的任一点,
上的任一点,![]() 是过点
是过点![]() 法线(即与过
法线(即与过![]() 点的切线垂直的直线),且
点的切线垂直的直线),且![]() ,
,![]() ,证明:直线
,证明:直线![]() 、
、![]() 与直线
与直线![]() 的夹角相等.
的夹角相等.
高考理科数学模拟示范卷(一)
数学(理科,江西专用) 参考答案
江西金太阳教育研究所数学研究室 编
一.选择题(本大题12个小题,每小题5分,共60分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | C | D | B | C | C | D | A | D | B | B |
二.填空题(本大题4个小题,每小题4分,共16分,)
13.0 14. ![]() 15.
15.
![]() 16.
16.
![]() .
.
三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,已知
,已知![]() ,且
,且![]() 、
、 ![]() 、
、![]() 成等比数列.
成等比数列.
(Ⅰ)求![]() 的值; (Ⅱ)若
的值; (Ⅱ)若![]() ,求
,求![]() 的值.
的值.
解:(Ⅰ)依题意,![]() ,由正弦定理及
,由正弦定理及![]() ,得
,得![]() .
.
![]() .
.
(Ⅱ)由![]() ,得
,得![]() ,即
,即![]() .由
.由![]() ,得
,得![]() (舍负)
(舍负)
∴![]() ,由余弦定理,得
,由余弦定理,得![]() ,∴
,∴![]() ,故
,故![]() .
.
18.(本小题满分12分)四个纪念币![]() 、
、![]() 、
、![]() 、
、![]() ,投掷时正面向上的概率如下表所示
,投掷时正面向上的概率如下表所示![]() .
.
| 纪念币 |
|
|
|
|
| 概率 |
|
|
|
|
这四个纪念币同时投掷一次,设![]() 表示出现正面向上的个数.
表示出现正面向上的个数.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在概率![]() 中,若
中,若![]() 的值最大,求
的值最大,求![]() 的取值范围;
的取值范围;
解:(Ⅰ)![]() 是
是![]() 个正面向上,
个正面向上,![]() 个背面向上的概率.其中
个背面向上的概率.其中![]() 的可能取值为
的可能取值为![]() .
.
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
∴![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 的数学期望为
的数学期望为![]() .
.
(Ⅱ)∵![]() ,∴
,∴![]() ,
,![]() .则
.则![]()
![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
 19.(本小题满分12分)如图,在斜三棱柱
19.(本小题满分12分)如图,在斜三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() 与底面
与底面
![]() 成
成![]() 的角,
的角,![]() .底面
.底面![]() 是边长为
是边长为![]() 的正三角形,
的正三角形,
其重心为![]() 点.
点.![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() .
.
(Ⅰ)求证:![]() 侧面
侧面![]() ;
;
(Ⅱ)求平面![]() 与底面
与底面![]() 所成的锐二面角的大小.
所成的锐二面角的大小.
解:(Ⅰ)延长![]() 交
交![]() 于点
于点![]() ,则
,则![]() ,即
,即![]() 为
为![]() 的中点.∵
的中点.∵![]() 为
为![]() 的重心,
的重心,
∴![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]() ,∴
,∴![]() ,故
,故![]() 侧面
侧面![]() .
.
(Ⅱ)作![]() 于
于![]() ,∴
,∴![]() 面
面![]() .∵侧棱
.∵侧棱![]() 与底面
与底面![]() 成
成![]() 的角,
的角,![]() .
.
∴![]() ,
,![]() ,
,![]() .作
.作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,∴
,∴![]() 为
为
所求二面角的平面角.又![]() ,
,![]() ,∴
,∴![]() ,在
,在
![]() 中,
中,![]() ,故所求锐二面角的大小为
,故所求锐二面角的大小为![]() .
.
20.(本小题满分12分)设![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求证:当![]() 时,
时,![]() 对任意正实数
对任意正实数![]() 成立.
成立.
(Ⅰ)解:当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() .∵当
.∵当![]() 时,
时,
![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() 的单调增区间是
的单调增区间是![]() ,
,![]() ;单调增区间是
;单调增区间是![]() .
.
(Ⅱ)证明:令![]() ,则
,则![]() .当
.当![]() 时,由
时,由![]() ,
,
![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上的最小值
上的最小值
是![]() ,故当
,故当![]() 时,
时,![]() 对任意正实数
对任意正实数![]() 成立.
成立.
21.(本小题满分12分)已知为正实数,数列![]() 由
由![]() ,
,![]() 确定.
确定.
(Ⅰ)对于一切的![]() ,证明:
,证明:![]() ;
;
(Ⅱ)若![]() 是满足
是满足![]() 的正实数,且
的正实数,且![]() ,证明:
,证明:![]() .
.
解:(Ⅰ)用数学归纳法证明:当![]() 时,
时,![]() ,
,![]() ,
,![]() 成立.
成立.
假设![]() 时结论成立,即
时结论成立,即![]() ,则
,则![]() ,即
,即![]() .
.
∴![]() ,∴
,∴![]() 时结论也成立,综上,对一切的
时结论也成立,综上,对一切的![]() ,
,![]() 成立.
成立.
(Ⅱ)![]() ,
,
∴![]() .当
.当![]() 时,
时,![]() ,与
,与![]() 矛盾,故
矛盾,故![]() .
.
∴![]()
![]() .
.
22.(本小题满分14分)已知常数列![]() ,点
,点![]() 是直角
是直角![]() 的直角顶点,顶点
的直角顶点,顶点![]() 在定直线
在定直线
![]() :
:![]() 上移动,斜边
上移动,斜边![]() 所在直线恒过定点
所在直线恒过定点![]() .
.
(Ⅰ)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设![]() 是轨迹
是轨迹![]() 上的任一点,
上的任一点,![]() 是过点
是过点![]() 法线(即与过
法线(即与过![]() 点的切线垂直的直线),且
点的切线垂直的直线),且![]() ,
,
![]() ,证明:直线
,证明:直线![]() 、
、![]() 与直线
与直线![]() 的夹角相等.
的夹角相等.
解:(Ⅰ)设![]() ,
,![]() ,依题意
,依题意![]() ,∴
,∴![]() ,即
,即![]() ①.
①.
又![]() 与
与![]() 共线,∴
共线,∴![]() ②. 由①②消去
②. 由①②消去![]() ,得
,得![]() .
.
(Ⅱ)由双曲线的对称性,不妨设![]() 是双曲线上位于
是双曲线上位于![]() 轴上方的点,由
轴上方的点,由![]() ,
,
得![]() ,∴
,∴![]() .故过点
.故过点![]() 的切线的斜率
的切线的斜率![]() ,而
,而![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() .设
.设![]() 是
是![]() 与直线
与直线![]() 的夹角,则
的夹角,则
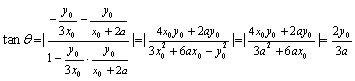 . 设
. 设![]() 是
是![]() 与直线
与直线![]() 的夹角,
的夹角, ![]() ,则
,则 .
.
∴![]() ,又
,又![]() ,∴
,∴![]() ,故直线
,故直线![]() 、
、![]() 与直线
与直线![]() 的夹角相等.
的夹角相等.