高考数学函数的图象测试

专题考案(1)函数板块 第3课  函数的图象

(时间：90分钟　满分：100分)

题型示例

作出下列函数的图象.

(1)y=x-2(x+1);　(2)y=10^lgx.

解　(1)当x≥2时，即x-2≥0时，y=(x-2)·(x+1)=x²-x-2=(x-)²-.

当x<2时，即x-2<0时，y=-(x-2)(x+1)=-x²+x+2=-(x-)²+.

所以y=.

这是分段函数，每段函数图象可根据二次函数的图象作出.如图1所示.

(2)当x≥1时，lgx≥0,y=10^lgx=10^lgx=x.

当0<x<1时，lgx<0,y=10^lgx=10^-lgx=，

所以y=.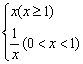

这是分段函数，每段函数可根据正比例函数或反比例函数作出，见图2.

点评　作不熟悉的函数图象，可以变形成基本函数再作图，但要注意，变形过程是否等价以及x,y的范围.因此必须以五类基本函数的图象为依托求解.

一、选择题(7×4′＝28′)

1．函数y=-e^x的图象　　　　　　　　　　　　　　　　　　　　　　　　　　  (　　)

A.与y=e^x的图象关于y轴对称

B.与y=e^x的图象关于坐标原点对称

C.与y=e^-x的图象关于y轴对称

D.与y=e^-x的图象关于坐标原点对称

2．若函数f(x)=a^x-b-1(a>0且a≠1)的图象通过第一、三、四象限，则有　　　　  (　　)

A．a>1且b<　　 B.a>1且b>0　　 C.0<a<1且b>0　　 D.0<a<1且b<0

3．已知函数y=log₂x的反函数是y=f^-1(x),则函数y=f^-1(1-x)的图象(如图3)是　　(　　)

		图3

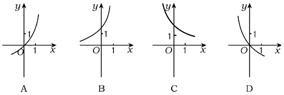4．定义在R上的函数y=f(x-1)是单调递减函数，其图象如图4所示，给出四个结论：

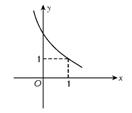①f(0)=1;　　　②f(1)<1;　　　③f^-1(1)=0;　　　④f^-1()>0.

其中正确命题的个数是 　　　　　　　　　　　　　　　　(　　)

A.1　　　　  B.2　　　　  C.3　　　　  D.4

5．设k>1,f(x)=k(x-1)(x∈R)在平面直角坐标系xOy中，函数y=f(x)的图象与

图4

x轴交于A点，它的反函数y=f^-1(x)的图象与y轴交于B点，并且这两个函

数的图象交于P点.已知四边形OAPB的面积是3，则k等于　　　(　　)

A.3　　　　  B.　　　　  C.　　　　  D.

6．现向一球形容器内匀速注入某种液体，在注入过程中容器的液面高度h随时间t的函数关系如图5　　　　 中所示.(其中球的半径为R)　　　　　　　　　　　　 (　　)

7．如图6,点P在边长为1的正方形的边上运动，设M是CD的中点，

则当P沿A—B—C—M运动时，点P经过的路程x与△APM的面积y

的函数y=f(x)的图象的形状大致是图7中的　　　　　　　 (　　)

			图6

	图7

二、填空题 (4×4′＝16′)

8．函数f(x)=的图象的对称中心是　　　　  .

9．若函数y=log₂ax-1(a≠0)的图象关于直线x=2成轴对称图形，则a=　　　　 .

10．某工厂八年来某种产品总产量C与时间t(年)的函数关系

如图8所示，则下列四种说法中正确的是　　　　  .

①前三年中产量增长速度越来越快

②前三年中产量增长的速度越来越慢

图8

③第三年后，这种产品停止生产

④第三年后，年产量保持不变

11．设f(x)表示-x+6和-2x²+4x+6中的较小者，则函数f(x)的最大值是　　　　 .

三、解答题(12′＋2×10′＋12′＝44′)

12．分别画出下列函数的图象.

(1)y=x²-2x-3;

(2)y=x²-2x;

(3)y=x²-2x-1.

13．设a∈R,试讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实数解的个数.

14．已知函数f(x)=m(x+)的图象与h(x)=(x+)+2的图象关于点A(0，1)对称.

(1)求m的值;

(2)若g(x)=f(x)+在(0,2)上是减函数,求实数a的取值范围.

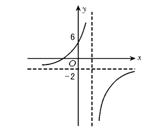
15．已知函数f(x)=(a≠0)的反函数f^-1(x)的图象如图9所示.

求a,b的值并写出f^-1(x)的解析式.

图9

四、思考与讨论 (12′)

16．设实数m、n满足4m²+n²=8，求：

的最小值．

参考答案

1．D　如图10所示，只有D项正确.

2．B　要使f(x)的图象经过第一、三、四象限，则必须有

3．C　∵y=log₂x其反函数y=f^-1(x)=2^x.

图10

则y=f^-1(1-x)=2^1-x=2·2^-x=2·()^x.

故排除A、B，又∵此函数过（0，2）,∴选C.

4．D　由y=f(x-1)的图象向左平移一个单位即得y=f(x)的图象.

5．B　如图11，∵f(x)=k(x-1)过定点A（1，0）知其反函数图象必过

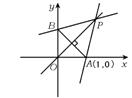B（0，1）,y=f(x)与f ′(x)=y交点位于直线y=x上.

图11

∴P,OP=·,

S_{四边形OAPB}=S_△OAP+S_△OBP=OP·AB=···=3.解得:k=.

6．C　在注入过程中，当0≤t≤t₀时，h随t的变化越来越慢；当t>t₀时，h随t的变化越来越快.

0≤x≤1 1<x≤2 2<x≤

7．A　经计算知y=

8．(-1,1)　f(x)=f(x)的对称中心是(-1,1).

9．　若y=log₂ax-1的图象关于x=2对称，则函数y=ax-1的图象也关于x=2对称，

∴=2a=

10．②③　∵在0到3之间经过曲线上的点和原点的直线的斜率k=随时间增加越来越小，故前三年中产量增长的速度越来越慢，第三年后产品总量没变，故这种产品停止生产.

11．6　在同一坐标系中作出y=-x+6,y=-2x²+4x+6的图象取函数值较大的即可.

12．解　如图12所示.

	图12

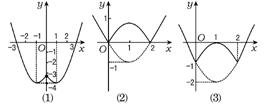13．解　原方程等价于:即等价于

以下只须考虑抛物线y=-x²+5x-3=-(x-)²+(1<x<3)与直线y=a的交点个数，

作出图象可知:

(1)当a∈(-∞,1)∪［,+∞］时，原方程无实数解.

(2)当a∈(1,3)∪{}时，原方程只有一个实数根.

(3)当a∈(3,)时,原方程有两个不同的实数根.

点评　本题重点考查函数图象的应用，数列结合的思想.

14．解　(1)设P(x,y)是h(x)图象上一点，点P关于A（0，1）的对称点为Q（x₀,y₀）,则x₀=-x,y₀=2-y.

∴2-y=m(-x-),∴y=m(x+)+2,从而m=.

(2)g(x)=(x+)+=(x+).

设0<x₁<x₂≤2,则g(x₁)-g(x₂)=(x₁+)-(x₂+)

=(x₁-x₂)+(a+1)·=(x₁-x₂)·>0,并且在x₁,x₂∈(0,2)上恒成立,

∴x₁x₂-(a+1)<0,∴1+a>x₁x₂,1+a≥4,∴a≥3.

15．解　由图象知f^-1(x)的图象过点(0,6),∴f(x)的图象必过点(6,0),

∴=6或a=0(舍去)　∴f(x)=.

又由图象知f^-1(x)的图象以y=-2为一条渐近线，因此y=f^-1(x)的值域为{yy≠-2},即函数f(x)的定义域为{xx≠-2},又∵f(x)= 的定义域为x≠,

∴=-2,∴b=4,∴f(x)=，求得f^-1(x)=(x≠3).

16．解　建立直角坐标系，动点(m,n)落在椭圆=1上，

而

表示动点(m,n)到两定点(0,2)与(2，2)的距离和．

∴最小值为两定点间的距离为2．