高考数学函数的定义域和值域测试

专题考案(1)函数板块 第1课 函数的定义域和值域

 (时间：90分钟　满分：100分)

题型示例

已知函数f(x)=log_a(x+1)的定义域和值域都是［0,1］，则a的值等于　　　　　 (　　)

A.　　　　B.　　　　C.　　　　D.2

分析　由题可知函数f(x)恒过(0,0),由于其定义域和值域都是［0,1］,故可判断a>1,且函数f(x)过(1,1)，即1=log_a(1+1)a=2,故选D.

答案　D

点评　仔细审题、数形结合是解答本题的关键.

一、选择题(8×3′＝24′)

1．函数y=的定义域是　　　　　　　　　　　　　　　　　　　  (　　)

A.［1,+∞　　 B.(,+∞)　　 C.［,1］　　 D.(，1)

2．已知函数f(x)=的定义域为A，函数y=f［f(x)］的定义域为B,则　　　　  (　　)

A.A∪B=B　　　　B.AB　　　　C.A=B　　　　D.A∩B=B

3．值域是(0,+∞)的函数是　　　　　　　　　　　　　　　　　　　　　　　　 ( 　 )

A.y=x²-x+1　　　B.y=()^1-x　　　C.y=+1　　　D.y=log₂x²

4．定义域为R的函数y=f(x)的值域为［a,b］，则函数y=f(x+a)的值域为　　　　　 (　　)

A.［2a,a+b］　　 B.［a,b］　　 C.［0,b-a］　　 D.［-a,a+b］

5．函数y=-1(-1≤x<0)的反函数是　　　　　　　　　　　　　　　　　　　  (　　)

A.y=　　　　　 B.y=-

C.y=　　　　D.y=-

6．若函数y=x²-3x-4的定义域为［0,m］，值域为［-,-4］，则m的取值范围是　 (　　)

A.(0,　　  B.［,4］　　  C.［,3］　　  D.［,+∞

7．函数y=x-3-x+1的值域是　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A.［0,4］　　　B.［-4,0］　　　C.［-4,4］　　  D.(-4,4)

8．函数y=的值域为　　　　　　　　　　　　　　　　　　　　　　  (　　)

A.［-,］　　 B.［-,0］　　 C.［0,］　　 D.(0,］

二、填空题 (5×3′＝15′)

9．设f(2^x-1)=2x-1，则f(x)的定义域为　　　　.

10．函数y=的定义域为(-∞,+∞),则实数a的取值范围是　　　　.

11．函数y=(x≥0)的值域是　　　　.

12．函数f(x)=x²+x+的定义域是［n,n+1］(n∈N^*)，则函数f(x)的值域中共有　　 个整数.

13．函数y=x-3+的值域是　　　　.

三、解答题(9′＋3×10′＋12′＋10′＝61′)

14．求函数y=的值域.

15．已知f(x)的定义域是［］,g(x)=f(x)+，试求y=g(x)的值域.

16．已知函数f(x)=log₃的定义域为(-∞,+∞),值域为［0,2］，求m、n的值.

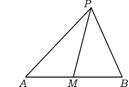
17．如图所示，A、B、P为平面上的三个点，M为线段AB的中点，

已知AB=4，PA+PB=6，求MP的最大、最小值.

18．已知函数f(x)的定义域是［a,b］，且a+b>0，求下列各函数的定义域.

(1)f(x²);

(2)g(x)=f(x)-f(-x);

(3)h(x)=f(x+m)+f(x-m)(m>0).

19．设f(x)=x²-2ax+2,当x∈［-1,+∞］时,f(x)≥a恒成立，求a的取值范围.

参考答案

1．D  若使函数有意义，则必有(3x-2)≥0,即0<3x-2≤1<x≤1.

2．D　y=f［f(x)］的定义域由确定.

3．B　逐一验证.

4．B　∵x∈R,x+a∈R,∴函数y=f(x+a)的值域与函数y=f(x)的值域相同且都为［a,b］.

故选B.

5．D　由y=得x²-1=log₃y,∵-1≤x<0

∴x=-,x、y互换得y=-

∵-1≤x<0,∴-1<x²-1≤0,∴<≤1

故原函数的反函数为:y=-.

6．C　作图判断.

7．C　作图或根据不等式a-b≤a-b确定.

8．C　先变形为acosx+bsinx=c的形式，由a²+b²≥c²确定.

9．(-1,+∞)　由u=2^x-1的值域确定.

10．［0,］　由ax²+4ax+3≠0恒成立确定，注意a=0的情况.

11．(-,3)　反解出x=f(y)，由x≥0求y的范围.

12．2n+2　f(x)=(x+)²+.由此可知，f(x)在［-,+∞］上为单调递增函数，故在［n,n+1］上f(x)与x存在一一对应关系.f(n+1)=(n²+3n+2)+,比f(n+1)小的整数中最大的是n²+3n+2,比f(n)小的整数中最大的是n²+n,f(x)的值域中的整数为n²+n+1,n²+n+2,…,n²+3n+2,故函数f(x)在［n,n+1］上的值域中整数的个数为(n²+3n+2)-(n²+n)=2n+2.

13．［4,+∞　y=x-3+x+1视为数轴上的点与-1,3两点距离之和的最小、最大值.由图可看出，最小值为4,不存在最大值.

14．解　令U=x²+2x-2=(x+1)²-3(U≠0),则y=.由二次函数的最小值为-3知U≥-3,U≠0,

当-3≤U<0,≤;

当U>0时,>0,故函数的值域为{yy≤}∪{yy>0}={yy≤}或y>0}.

点评　本题利用换元法，结合二次函数的最值;对值域的求法要求较高，在练习过程中要仔细体会.

15．解　令=t，则≤1-2f(x)≤，即≤t≤.

则y=g(x)=F(t)=+t=-(t-1)²+1,函数y=F(t)在［］上为增函数，故

F()≤y≤F(),F()=,F()=，故y=g(x)的值域为［,］.

16．解　令u=，其定义域为(-∞,+∞)，值域由题设知为［1,9］,

由u=得(u-m)x²-8x+(u-n)=0.

因为x∈R,且设u-m≠0,则Δ=(-8)²-4(u-m)(u-n)≥0.

即u²-(m+n)u+(mn-16)≤0,又1≤u≤9.

故(u-1)(u-9)≤0，即u²-10u+9≤0

∴，解得m=n=5.

若u-m=0,即u=m=5时，x=0满足要求.故m=n=5.

17．解　因为PA-PB≤AB(P、A、B三点共线时取“=”号)，设PA=x,则x-(6-x)≤4，

即1≤x≤5.

由平面几何知识知(2MP)²+AB²=2(PA²+PB²)，即

MP²=［x²+(6-x)²］-4=x²-6x+14=(x-3)²+5　(1≤x≤5).

当x=3时,MP_min＝；当x=1或5时，MP_max=3.

18．解　(1)依题意，由知b>0且b>a.

则a≤x²≤b，得当a≤0时，f(x²)的定义域为［］；

当a>0时，f(x²)的定义域为.

(2)由*

∵a>-b,b>-a，当a>0时，不等式*解集为，此时函数g(x)不存在.

当a=0时，不等式*解集为{0},此时函数g(x)的定义域为{0}.

当a<0时，不等式*的解集为［a,-a］，此时函数g(x)的定义域为［a,-a］.

(3)由

因为m>0,所以a-m<a+m,b-m<b+m.

又a-m<b+m,要使函数h(x)的定义域为非空集合，只需a+m≤b-m，

即0<m≤,此时函数的定义域为［a+m,b-m］.

19．解　f(x)=x²-2ax+2=(x-a)²+2-a²,f(x)图象的对称轴为x=a.为使f(x)≥a在［-1,+∞上恒成立，只需f(x)在［-1,+∞上的最小值比a大或等于a即可.

(1)a≤-1时,f(-1)最小,解,解得-3≤a≤-1.

(2)a≥-1时,f(a)最小，解,解得-1≤a≤1.综上得:-3≤a≤1.