高考数学复习高一下测试试题
数学试卷 命题人 薛林生 审定 俞光军
一、选择题（每小题5分，共20分）
1．在△ABC中，根据下列条件解三角形，则其中有两个解的是 （ ）
A．b = 10，A
= 45°，B = 70° B．a
= 60，c = 48，B
= 100°
C．a = 7，b
= 5，A = 80°
D．a = 14，b
= 16，A = 45°
2．下列条件中，能得出△ABC是等腰直角三角形的是 （ ）
A．
B．
C．
D．
3．在正项等比数列{an}中，a1和a19为方程x2-10x+16=0的两根，则a8a10a12= （ ）
A．32 B．64 C．±64 D．256
4．已知s
是等差数列｛a｝的前n项和，若a
+a
+a
是一个确定的常数，则数列｛s｝中是常数的项是
（ ）
A．s
B． s
C． s
D．s
二、填空题（每小题5分，共50分）
5．2，8的等差中项是 等比中项是
6．
7．已知数列
的前n项和
，则通项
8．在△ABC中，若a＝
，A＝60°，那么这三角形的外接圆周长为
9．在△ABC中，若AB＝5，BC＝7，AC=8，那么AC边上中线BD=
10．在△ABC中,
,则角A= .
11．设等比数列
的前n项和为Sn，若
，则
12．是各项都是正数的等比数列，若
成等差数列，则
的值为
13．设函数y=f（x）的定义域为R，数列的通项
，下列命题：
①若函数y=f（x）在
上单调递增，则数列也单调递增；②若数列单调递增，则函数y=f（x）在上单调递增；③若f（x）是一次函数，则数列是等差数列；④若数列是等差数列，则函数y=f（x）是一次函数；⑤若函数f（x）是指数函数，则数列是等比数列；⑥若数列是等比数列，则函数y=f（x）是指数函数。
其中正确命题的序号为
14．已知
，则
=
三、解答题（共90分）
15．（14分）已知{an}为等差数列，
，其前n项和为
，若
，
（1）求数列{an}的通项；（2）求的最小值，并求出相应的n值。
16．（14分）在△ABC中，角A、B、C的对边分别为a、b、c.已知a+b=13，c =7，
且
，(1) 求角C的大小；（2）求△ABC的内切圆面积.
17．（14分）已知数列
，
设
，数列
，
（1）求证：
是等差数列； （2）求数列
的前n项和Sn；
18. （16分）如图，为求河对岸某建筑物的高AB，在地面上引一条基线CD，设
| 第一次 | 第二次 | 第三次 | 平均值 | |
| α | 74° | 73.6° | 77.4° | |
| β | 59° | 60.4° | 60.6° | |
| γ | 29° | 30.4° | 30.6° | |
| CD | 59.1m | 59.7m | 61.2m |
∠ADC=α，∠ACD=β，∠BDA=γ。为了使测量尽量准确可靠，进行了三次测量，所得数据如下：
根据数据计算建筑物的高AB。（精确到0.1m）
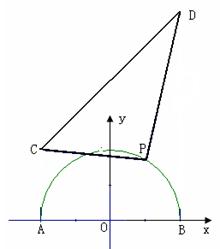
19．（16分）直角坐标系中，A、B、C、D四点坐标分别为（-1，0），（1，0），（-1，1），
（1，3），点P在以AB为直径的圆上且位于x轴上方，当点P在半圆上变化时，选择适当的自变量，将△PCD的面积表示为该自变量的函数；并求出该函数的值域。
 |
20．（16分）江苏省淮阴中学2000年高一招收新生1100人，由于办学质量高，高考成绩突出，从2001开始报考淮阴中学的学生人数逐年增加，为了满足社会需求，每年适当增加招生计划，但为了保证质量又要严格控制招生人数，经研究每年新增的招生人数不得超过20人，
（1）求从2000年到2010招收高一新生总数，累计最多可达多少人？
（2）若某年招生人数达到1288人，求从2000起累计招生人数的最小值。
高考数学复习高一下测试试题
数学试卷答案
一、选择题 DABD
二、填空题
5．5、
6．
7．
8．
9．
10．
11．
12． 
13．①③⑤ 14．10
三、解答题
15．解：(1)
由
，得d=2 ………………4分
………………8分
（2）
最小
………………14分
16.．(1) 解：∵A+B+C=180°
由
…………2分
∴
………………4分
整理，得
解 得：
∵
∴C=60°
………………6分
（2）解：由余弦定理得：c2=a2+b2－2abcosC，即49=a2+b2－ab，∴
由条件a+b=13得 ，a=5,b=8或a=8,b=5 ………………10分
∴ 
………………12分
内切圆半径r=
，
………………………14分
17．解：（1）由题意知，
……………………4分
∴数列
的等差数列
……………………6分
（2）由（1）知，
…………………………8分
于是
两式相减得
……………………12分
……………………14分
18． 平均值填对 ………………4分
中，算出
………………9分
中，算出
………………14分
答：建筑物高AB=42.4m ………………16分
19．解：作
交于Q，设
………………2分
梯形AQPC的面积，
梯形BQPD的面积，
,梯形ABDC的面积，
,
的面积，
………………12分
该函数的值域为
………………16分
20．解：（1）从2000年起，每年最多招生人数为1100，1120，1140，…构成等差数列
，即从2000年到2010年，累计招生人数最多可达13200人
………………4分
（2）设第n年招生人数达1288人，从2001开始的每年招生人数分别记为：
，
，
的最小值为1288-20，
的最小值为
所以，的最小值构成一个等差数列，公差d=20， ………………8分
，
………………12分
为所求最小值。
………………16分