湖南资兴市立中学高三数学模拟(一)

湖南资兴市立中学02-03年高三数学模拟(一)

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第Ⅰ卷1至2页，第Ⅱ卷3至8而，共150分，考试时间120分钟.

第Ⅰ卷（选择题 共50分）

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合韪要求的.

（1）　　　 已知函数y=a^x的图象与其反函数的图象有交点，则a的取值范围是

（A）（0，+∞）　　（B）（0，1）　 （C）（1，+∞）　 （D）（0，1）∪（1，∞）

（2）　　　 设f：x→x²是集合A到集合B的映射，如果B=｛1，2｝，则A∩B只可能是

（A）φ　　 （B）φ或｛2｝　 （C）φ或｛1｝　　　　（D）｛1｝

（3）　　　 复数（）³的值是

（A）-i　　　　  (B)I　　　 (C)-1　　　　(D)1

（4）　　　 不等式组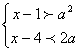有解，则实数a的取值范围是

（A）（-1，3）（B）（-3，1）（C）（-∞，-1）∪（3，+∞）（D）（-∞，-3）∪（1，+∞）

（5）　　　 等比数列｛a_n｝中，公比为q，则“a₁＞0，且q＞1“是”对于任意自然数n,都有a_n+1＞a_n”的

（A）充分非必要条件 （B）必要非充分条件 （C）充要条件（D）非充分非必要条件

（6）　　　 你手中的一支笔，在空间任意移动，在你课桌桌面所在的平面上总有这样的直线，它与你手中的笔所在直线

（A）平行　　 （B）垂直　　（C）相交　　（D）异面

（7）　　　 某学校餐厅供应师生饭菜，每位师生可在提供的菜肴中任选二荤二素共4种不同的品种，现餐厅准备了5种不同的荤菜，若要保证每位师生有200种以上的不同选择，则餐厅至少需准备不同品种的素菜

（A）5种　　　（B）6种　　（C）7种　　　（D）8种

（8）　　　 把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半，纵坐标扩大到原来两部，然后把图象向左平移个单位，则所得图形表示的函数解析式为

（A）y=2sin2x　　　 (B)y=-2sin2x　　 (C)y=2cos(2x+)　(D) y=2cos(+)

（9）　　　 已知数列｛a_n｝的前n项和S_n=n²+n，则过点A（k，a_k）B（k+1，a_k+1）(k∈N)的直线的斜率是

（A）1　　 （B）2　　 （C）3　　  （D）4

（10）　 设双线曲（a＞，b＞）的一条准线与两渐近线相交于A、B两点，相应的集点为F，若ΔABF为直角三角形，则双曲线的离心率为

（A）3　　 （Ｂ）2　　　 （C）　　 （D）

二、填空题：本大题共4小题，每小题4分，共填在题中的横线上.

（11）已知（4^x－）⁵展开式中第四项的值是-80，则x=　　　　　 .

（12）圆锥的母线与底面所成的角为30°，轴截面面积为Q，则圆锥的侧面积　　　

（13）有一系列中心在原点，以坐标轴为对称轴的椭圆，它们的离心率分别为、（）²、（）³、…、（）ⁿ、…（n∈N），且都以x=1为准线，则所有这些椭圆的长半轴之和为

　　　　 

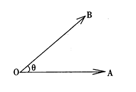
（14）如图，任意两个非零向量a、b，a=，、b=，

θ=∠AOB（O≤θ≤π），当θ=时，记作a⊥b，定义运算“*”为：

a*b=│a│·│b│·cosθ，其中│a│、│b│分别是向量a、b的模，

根据上述定义的运算，某同学得到以下三个结论：

①a*b=b*a

②a*a=│a│²

③a*b=Oa⊥b

其中正确结论的序号是　　　　　　　　 (请你把所有正确的结论的序号都填上).

三、解答题：本大题共6小题，共84分.解答应写出文字说明、证明过程或演算步骤.

(15)（本小题满分12分）

ΔABC中，若角A、B、C所对边分别为a、b、c且a、b、3c成等比数列，又A－C=，

求A、B、C的值.

（16）（本小题满分12分）

复数集合M=｛Z││Z│≤2｝、｛Z││Z-4+i│=│Z-43i│｝，试求M∩N中的元素Z的辐角主值的范围。

（17）（本小题满分14分）

已知涵 数f（x）=，g（x）=2x-m

（Ⅰ）当m=-1时，解不等式f（x）＜g（x）；

（Ⅱ）如果对满足│m│＜1的一切实数m,都有f（x）＞g（x）恒成立，求x的取值范围.

（18）（本小题满分16分）

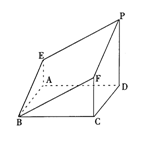
如图，ABCD为正方形，AF、CF、DP均垂直平面ABCD，

且AE=CF=DP，又DP=AB=2

（Ⅰ）求证：P、E、B、F四点共面；

（Ⅱ）求平面PEBF与平面ABCD所成的角的余弦值；

（Ⅲ）求该几何体PEBF－ABCD的体积；

（Ⅳ）（理科考生做文科考生不做），延长AE至Q，使

EQ=EA，求Q到平面PEBF的距离.

19．（本小题满分14分）

据2000年4月份的“光明日报”报道，水土流失是我国西部开发中最突出的生态问题，全国9100万亩的山坡耕地需要退耕还林，其中西部地区占70%，国家确定2000年底在西部地区退耕土寺面积为515万亩，以后每年退耕土地面积递增12%.

（Ⅰ）试问从2000年起，到哪年年底西北地区基本解决退耕还林问题？（用四舍五入精确到年）

（Ⅱ）为支持退耕还林工作，国家决定对已退耕还林地每年每亩朴助20元，试问西北地区基本解决退耕还林时，国家财政共支付约多少万元.（用四舍五入精确到万元）

（lg1.12=0.05、lg2.484=0.40、1.12⁹=2.80）

（20）（本小题满分16分）

定义在（-1，1）上的函数f（x）满足（1）对任意x、y∈（-1，1）都有f（x）+ f（y）=

f（）；

（2）当x∈（-1，0）时，有f（x）＞0

（Ⅰ）判定f（x）在（-1，1）上的奇偶性，并给予证明；

（Ⅱ）判定f（x）在（-1，0）上的单调性，并给予证明；

（Ⅲ）求证：f（

（Ⅳ）（理科考生做文科考生不做）求证：