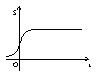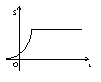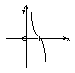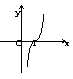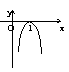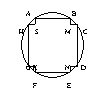高三数学上学期代数综合练习(一)

代数综合练习(一)

　2002.4　 班级：_______________；姓名：___________________；成绩：_______________

一. 选择题：(每小题4分，共4×10 = 40分)将正确答案填入下表中

1	2	3	4	5	6	7	8	9	10

1. 设集合A = {x 1 < x £ 2}, B = {x x－a > 0}, 当AB = A时，实数a的取值范围是
　　　(A) [2 , +¥)　 (B) (－¥ , 1]　 (C) (－¥ , 1)　 (D) (2 , +¥)　

2. 下列函数：①y = 3;②y = ()^1－x ;③y =; ④y =.其中值域是(0,+ ¥)的函数有
　　　(A) 1个　　(B) 2个　　(C) 3个　　(D) 4个

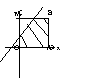
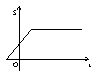
3. 如图，四边形OABC是正方形，在直线l : y = x + t下方的面积为S. 当

直线l由下而上匀速移动时，面积S关于t的函数图象是

　　　 (A)　　　　　　　  (B)　　　　　　  (C)　　　　　　　　 (D)

4. 定义在R上的偶函数f (x)，满足f (3 + x) = f (3－x)，且在[－3,0]上单调递减，设a = f (－1.5), b = f (7), c = f (4)，则a, b, c的大小顺序为
　　　(A) b < c < a　 (B) a < b < c　 (C) b < a < c　 (D) c < b < a　

5. 奇函数f (x)的定义域是R，函数g (x) = x² + f (x－1) + f (x + 1). 若g (1) = 4，则g (－1)的值等于
　　　(A) －1　; (B) －2　; (C) －3　; (D)无法确定　;

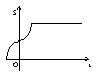
6. 已知函数y = f (x)的图象如右图，则函数y = log_0.2f (x)的图象是

　　  (A)　　　　　　  (B)　　　　　　  (C)　　　　　　　  (D)　

7. 不等式log₃ x－ <－1的解集是

　　  (A) (0,1)　; (B) (0,)　; (C) (,+¥)　; (D) (0, )(,)　;

8. 若a² + b² = 1，则(1 + ab)(1－ab)的最大、最小值分别是
　　　(A) 1和　; (B) 1和0　; (C) 和0　; (D) 和　;

9. 已知函数f (x) =－2x + 1对任意正数e，使得f (x₁)－f (x₂) < e成立的一个充分但不必要条件是
　　　(A) x₁－x₂ <e　; (B) x₁－x₂ <　; (C) x₁－x₂ <　; (D) x₁－x₂ >　;

10. 原市话资费为每3分钟0.18元，现调整为前3分钟资费为0.22，超过3分钟，每分钟0.11元，与调整前相比较，一次通话提价的百分比
　　　(A)不会高于70% (B)会高于70%而不会高于90% (C)不会低于10% (D)高于30%而低于100%

二. 填空题：(每小题4分，共4×5 = 20分)

11. 方程4^x + 6^x = 2×9^x的解集是_________________ .

12. 函数y = x²－5x + 6 (x < 2)的反函数是__________________ .

13. 将桶1的水到入桶2，开始时桶1中有水a升，t分钟后剩余的水符合指数衰减曲线y₁ = ae^-nt, 那么桶2中的水就是y₂ = a－ae^-nt. 假设过5分钟两桶的水相等，则再过__________分钟桶中1的水只有.

14. 设(－¥,a)是函数f (x) = (x¹2)的反函数的一个单调递增区间，则实数a的取值范围是____.

15. 设函数f (x) = xx + bx + c，给出四个命题：①c = 0时，f (x)是奇函数；②b = 0, c > 0时，方程f (x) = 0只有一个实根；③f (x)的图象关于点(0, c)对称；④方程f (x) = 0至多有两个实根. 其中正确命题的序号是______________________ .

三. 解答题：(每题10分，共40分)

16. 解关于x的不等式：> (a > 0且a¹1)

17. 有一种变压器的铁芯的截面是正十字形，即矩形ABEF与矩形CDGH全等，且AS = KF = HS = MC. 为保证所需的磁通量，要求正十字形面积为4cm². 为了使绕铁芯所用的铜线最省，即正十字形的外接圆周长最小，应如何设计正十字形的长和宽(即确定AB与BE的长度)?
18. 设f (x)是定义在[－1, 1]上的奇函数，g (x)的图象与f (x)的图象关于直线x = 1对称，而当xÎ[2, 3]时，g (x) =－x² + 4x + c (c为常数).

　 (1) 求f (x)的表达式；

　 (2) 对于任意x₁, x₂ Î [0, 1]且x₁ ¹ x₂，求证：f (x₂)－f (x₁) < 2x₂－x₁；

　 (3) 对于任意x₁, x₂ Î [0, 1]且x₁ ¹ x₂，求证：f (x₂)－f (x₁) < 1.

19. 已知f (x)是定义在[-1, 1]上的奇函数，且f (1) = 1. 若a, b Î [-1, 1], a + b ¹ 0有> 0.

　 (1)判断函数f (x)在[-1, 1]上是增函数还是减函数，证明你的结论；

　 (2)解不等式f (x +) < f ()；

　 (3)若f (x) < m²－2am + 1对一切x Î [－1, 1], a Î [－1, 1]恒成立，求实数m的取值范围.
参考答案：一. B;A; C;C;B;D;D;A;C; B;

　　二. 11.x=0; 12.y=1/2(5-Ö(1+4x)) (x>0); 13 10; 14. a £－2; 15.①②③;

　　三. 16. 0<a<1时,1<x<(1+Ö5)/2 , a>1时, 0<x<1 or x > (1+Ö5)/2 ;

　　　 17提示：连结AE, 设AB = x, BE = y, 直径AE = d，圆周长为c，则2xy - x² = 4Ö5, d = Ö(x² + y²), c = pd∴c = pÖ(x² + y²) = pÖ[x² + (x²+4Ö5/2x)² =pÖ[5x²/4 + 20/x² + 2Ö5] > pÖ(10+2Ö5), 当且仅当x = 2, y = Ö5 + 1时等号成立∴设计正十字形的长、宽分别为Ö5 + 1 cm, 2cm时，其外接圆的周长最小.

　　　 18. 提示：(1) f (x) = -x², xÎ[-1, 0); f (x) = x², xÎ[0, 1]; (2) ∵xÎ[0, 1]且x₁ ¹ x₂∴0 < x₁+x₂<2∴ f (x₂)－f (x₁) = (x₂-x₁)(x₂+x₁) < 2x₂ - x₁; (3) ∵xÎ[0, 1] ∴0<x₁²<1, 0<x₂²<1∴-1<x₂² - x₁² < 1∴x₂² - x₁² < 1∴f (x₂)－f (x₁) < 1.

　　　 19. 提示：(1)任取-1 < x₁ < x₂ < 1，则-x₂ Î[-1, 1] ∵f (x)是奇函数∴f (x₁) - f (x₂) = f (x₁) + f (-x₂) = [f (x₁) + f (-x₂)]/(x₁ - x₂)·(x₁ - x₂) < 0∴f (x₁) < f (x₂) ∴f (x)在[-1, 1]上是增函数；(2)不等式解集为[-3/2, -1); (3) ∵f (x)在[-1, 1]上是增函数，且f (1) = 1∴对一切x Î [－1, 1]有f (x) < 1∴要使对一切x Î [－1, 1], a Î [－1, 1] f (x) < m²－2am + 1恒成立，只须m² - 2am + 1 > 1成立∴m² - 2am > 0令g (a) = -2ma + m², a Î [-1, 1]，要使g (a) > 0在[-1, 1]上恒成立，只须g (a)在[-1, 1]上的最小值大于等于零，从而求出m < -2 or m = 0 or m > 2.