西安中学高三年级四月模拟考试数学试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间120分钟。
参考公式：
正棱台、圆台的侧面积公式
；其中c’，c分别表示上、下底面周长，l表示斜高或母线长。
台体的体积公式
，其中S’，S分别表示上、下底面面积，h表示高。
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一个是符合题目要求的。
1．线段AB的长为6cm，点P在BA的延长线上，PB=9cm，那么，P分线段AB所成的比等于（ ）
A．1/3 B．3 C．-1/3 D．3
2．（理）已知f (cosx)=sin2x，则
（ ）
A．-1/2 B．1/2 C．
D．
（文）已知
，则f（2）=（
）
A．0 B．3 C．0或3 D．2
3．复数z在复平面上对应的点为M，则复数1/z在复平面上对应的点只可能为（）
A．E B．F C．M D．N
4．记P=1，O=sin1，R=gh1，则它们的大小关系为（ ）
A．P<Q<R B．R<P<Q C．Q<P<R D．Q<R<P
5．设P，Q是两个集合，定义：
若P{4，5，6，7}，Q={3，4，5}，则P×Q的元素个数是（ ）
A．3 B．4 C．7 D．12
6．圆锥的侧面展开图是一个半径为12的半圆，这个圆锥的内切球的体积为（ ）
A．
B．
C．
D．
7．若函数sinx+f（x）在区间
内单调递增，则f(x)可以是（ ）
A．1 B．cosx C．sinx D．-cosx
8．安排甲、乙、丙三人周一至周六值班，每人值班两天，但周一不能排甲，周六必须排乙，则不同的排法种数共有（ ）
A．18 B．12 C．24 D．36
9．如果x、y是实数，那么x≠y是cosx≠cosy的（ ）
A．充分而非必要条件 B．必要而非充分条件
C．充要条件 D．既不充分也不必要条件
10．（理）双曲线
的离心率
，则k的取值范围是（ ）
A．（0，12） B．（8，20） C．（-12，0） D．（-20，-8）
（文）双曲线的离心率为2，则k 的取值是（ ）
A．12 B．-12 C．-8 D．-20
11．已知函数是定义域为R的偶函数，且是周期为2的函数，当
时，f(x)=x则f(3/2) 的值为（ ）
A．11/2 B．-11/2 C．-5/2 D．5/2
12．（理）方程
的根为
，方程
的根为
，则
（ ）
A．
B．
C．
D．π
（文）下列各式中，值为1/2的是（ ）
A．
B．
C．
D．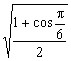
二、填空题：本大题共4小题：每小题4分，共16分。
13．设函数
且满足
的x的值为_______________。
14．二项式
展开式中a的一次幂的系数为___________________。
15．在棱长为1的正方体
中，对角线在六个面上的射影长度总和为_____________。
16．抛物线
的顶点与焦点关于点（0，1）对称，则a=____________。
三、解答题：本大题共6小题；共74分。解答应写出文字说明、证明过程或演算步骤。
17．（文）（12分）设复数
如果z的最大值为2，求实数k
（理）（12分）设
是模为1的两个复数，
，且
，
的虚部为
的实部为
。
求（1）
的值：
（2）
的值。
18．（理）（12分）已知数列
（1）求数列
的通项公式：
（2）设
，
，求
。
（文）（12分）设数列的首项为
且
（1）求数列的通项
；
（2）若数列的前n项和
，求n的最小值；
（3）问当n为何值时，
最小值，并求这个最小值。
19．（12分）已知：四棱锥P—ABCD的底面为正方形，PA⊥底面ABCD，E、F分别为AB、PD的中点，PA=a，二面角P—CD—B为45°。
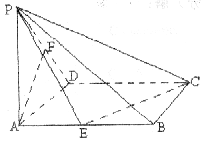
（1）求证：AF∥平面PCE：
（2）求证：平面PCE⊥平面PCD；
（3）求点D到平面PCE的距离。
20．（12分）某渔业公司今年初用98万元购进一艘渔船用于捕涝。第一年需各种费用12万元，从第二年开始包括维修费在内，每年所需费用均比上一年增加4万元，该船捕捞总收入预计每年5万元。
（1）该船捕捞几年开始盈利（即总收入减去成本及所有费用之差为正）？
（2）该船捕捞若干年后，处理方案有两种：①年平均盈利达到最大值时，以26万元的价格卖出；②当盈利总额达到最大时，以8万元的价格卖出。
21．（12分）已知函数
，设其反函数为
，对于给定的正数k，试求解关于x的不等式
22．（14分）设双曲线C的中心在原点，以抛物线
的顶点为双曲线的右焦点，抛物线的准线为双曲线的右准线。（1）试求双曲线的方程：
（2）设直线l：y=kx+1与双曲线C交于A、B两点。试问：①当k为何值时，以AB为直径的圆经过原点；
②（理科做，文科不做）是否存在这样的实数k，使A、B两点关于直线y=ax对称（a为常数）。若存在求出k的值；若不存在，请说明理由。
西安中学高三年级四月模拟考试数学答案
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | C | D | B | D | A | B | CB | D | C |
二、填空题（每小题4分，共16分）
13．3 14．35 15．
16．
三、解答题
17（文）（12分）
解：
又∵k≥0，∴当cosx= -1时，
，解得k=3/2
17．（理）（12分）
解：（1）由题设
，
（2）∵，∴
，
∴
，
∴
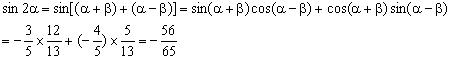
18．（理）
解（1）由
得
∴数列
是以2为首项，2为公比的等比数列，
∴
∴
（或用归纳法，需证明）
（2）
∴
，
∴
18．（文）
解：（1）∵
∴是等差数列。公差
∴
（2）由
得n>26，∴满足的最小值为27
（3）令
得
，∴当n=13时，最小，最小值
。
19．（12分）
解：（1）取PC的中点为G，连结FG、EG，∵
，
，∴
，∴四边形AFGE为平行四边形，
∴AF//EG，又∵
，∴AF//平面PCE。
（2）∵PA⊥平面ABCD，AD⊥DC∴PD⊥DC
∴∠PDA为二面角P—CD—B的平面角，∴∠PDA=45°即△PAD为等腰直角三角形
又∵F为PD的中点∴AF⊥PD……①
由DC⊥AD，DC⊥PD，
得DC⊥平面PAD，而
，∴AF⊥DC②
由①②得AF⊥平面PDC，而EG//AF，∴EG⊥平面PDC，又
，
∴平面PCE⊥平面PDC。
（3）过点D作DH⊥PC于H，∵平面平PCE⊥平面PDC
∴DH⊥平面PEC
即DH的长为点D到平面PEC的距离。
在Rt△PAD中，PA=AD=a，
在Rt△PDC中，
即点D到平面PCE的距离为
。
20．解：（1）设n年后开始盈利，盈利y元，则
令y>0解得
∴3≤n≤17
即捕捞3年后开始盈利：
（2）①平均盈利为
②
,当n=10时,
,
∴经过10年捕捞盈利额最大，共盈利102+8=110万元
两种方案盈利额相同，但方案②时间长3年，所以方案①合算。
21．解：
，x∈R，∴
所解得
，∴
原不等式转化为
，且k>0，-1<x<1
∴
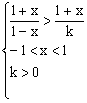解得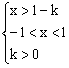
①当1-k<-1，即k>2时，不等式解集为{x-1<x<1}
②当-1≤1-k＜1 即0＜k≤2时，不等式解集为{x-k<x<1}。
22．（14分）
解：（1）抛物线方程为
，∴抛物线顶点为
准线方程为
，依题意，在双曲C中有
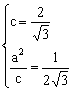解之得
，
∴双曲线的C方程为
（2）①由
得
由已知
，△>0得
设
，∵OA⊥OB，则
∵
∴
即
由韦达定理知
代入化简得k=±1
∴k=±1以AB为直径的圆过原点。
③若存在实数k，使A、B两点关于直线y=ax对称，则
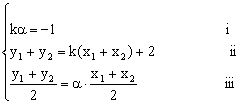
由i，ii有
又∵
代入上式化简得
2ak=6
∴ak=3与i矛盾.
故不存在实k，使A、B两点关于直线y=ax对称。