湖南省十校联考理科数学试题
命题人:刘菊秋 南方中学
谭祖荣 衡阳一中
何华清 涟源一中
黄小红 株洲县五中
一、选择题(本大题共10小题,每小题5分,共50分;在每小题给出的四个选项中,有且只有一项是符合题目要求的)
1、已知![]()
A.![]() B.(
B.(![]() ) C.
) C.![]() D.(
D.(![]() )
)
2、![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、已知平面上三点A、B、C满足![]() ,
,![]() ,
,![]() ,则
,则![]() 的值等于
的值等于
A.25 B.24 C.-25 D.-24
4、设a,b,c是空间三条直线,![]() ,
,![]() 是空间两个平面,则下列命题中,逆命题不成立的是
是空间两个平面,则下列命题中,逆命题不成立的是
A.当c⊥![]() 时,若c⊥
时,若c⊥![]() ,则
,则![]() ∥
∥![]()
B.当![]() 时,若b⊥
时,若b⊥![]() ,则
,则![]()
C.当![]() ,且c是a在
,且c是a在![]() 内的射影时,若b⊥c,则a⊥b
内的射影时,若b⊥c,则a⊥b
D.当![]() ,且
,且![]() 时,若c∥
时,若c∥![]() ,则b∥c
,则b∥c

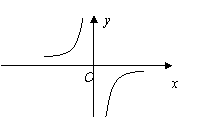 5、函数y=f(x)与y=g(x)的图象如下图:
5、函数y=f(x)与y=g(x)的图象如下图:
![]()
![]()
 则函数y=f(x)g(x)的图象可能为
则函数y=f(x)g(x)的图象可能为
A B C D
6、 ![]()
A.等腰三角形 B. 直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
7、 若(x![]() –
–![]() )6的展开式中的第五项是
)6的展开式中的第五项是![]() , 设Sn = x –1 + x –2 + … + x – n , 则
, 设Sn = x –1 + x –2 + … + x – n , 则![]() Sn等于
Sn等于
 A.1 B.
A.1 B. ![]() C.
C. ![]() D.
D.![]()
8、如右图所示,在单位正方体![]()
的面对角线![]() 上存在一点
上存在一点![]() 使得
使得![]() 最
最
短,则![]() 的最小值为
的最小值为
A.2 B.![]() C.
C.![]() D.
D. ![]()
9、椭圆![]() 与直线
与直线![]() 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为![]() ,则 值
,则 值
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10.由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二、填空题(本大题共5小题,每小题4分,共20分)
11、在条件 下,
下, ![]() 的取值范围是________ 。
的取值范围是________ 。
12、将函数y=f(x)sinx的图象向右平移![]() 个单位后,再作关于x轴对称的曲线,得到函数
个单位后,再作关于x轴对称的曲线,得到函数
y=1-2sin2x, 则f(x)=________.
13、![]()
14、在数列![]() 在直线
在直线![]() 上,
上,![]() ,则
,则![]() 。
。
15、已知f ( x )是定义在实数集上的函数,且f ( x + 2)
=![]() , 若f ( 1 ) = 2 +
, 若f ( 1 ) = 2 + ![]() ,
,
则f ( 2005) = .
三、解答题(本大题共6个小题,共80分)
16.(本小题满分12分)已知向量![]() =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量![]() (2,0)所成角为
(2,0)所成角为![]() ,其中A, B, C是⊿ABC的内角.
,其中A, B, C是⊿ABC的内角.
(1)求角B的大小;
(2)求sinA+sinC的取值范围.
17、(本小题满分12分)下表为某体育训练队跳高成绩的分布,共有队员40人,成绩分为1~5五个档次,例如表中所示跳高成绩为4分,跳远成绩为2分的队员为5人。将全部队员的姓名卡混合在一起,任取一张,该卡片队员的跳高成绩为x,跳远成绩为y,设x,y为随即变量(注:没有相同姓名的队员)
(1)求![]() 的概率及
的概率及![]() 且
且![]() 的概率;
的概率;
(2)求![]() 的值;若y的数学期望为
的值;若y的数学期望为![]() ,求m,n的值.
,求m,n的值.
| y x | 跳 远 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 跳 高 | 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 2 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 4 | 3 | |
| 2 | 1 | m | 6 | 0 | n | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
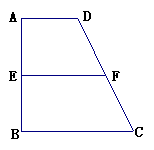
18、(本题满分14分)已知梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ∥
∥![]() ,
,![]() ,
,![]() 是
是![]() 的中点。沿
的中点。沿![]() 将梯形
将梯形![]() 翻折,使平面
翻折,使平面![]() 平面
平面![]() (如图)。
(如图)。
(1) 当![]() 时,求证:
时,求证:![]() ;
;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;
的最大值;
(3) 
 当
当![]() 取得最大值时,求二面角D-BF-C的大小。
取得最大值时,求二面角D-BF-C的大小。
19.(本小题满分14分)
|
(1)求动点Q的轨迹方程;
(2)设过点A的直线与点Q的轨迹交于E、F两点,
![]() ,求直线
,求直线![]() E、
E、![]() F的斜率之和。
F的斜率之和。
20.(14分)已知等差数列![]() 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列![]() 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,![]() ,且
,且![]() .
.
(1)求a的值;
(2)若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() ,求b的值;
,求b的值;
(3)在(2)中,记![]() 是所有
是所有![]() 中满足
中满足![]() ,
, ![]() 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记![]() 为
为![]() 的前n项和,
的前n项和,![]() 是
是![]() 的前n项和,求证:
的前n项和,求证:![]() ≥
≥![]()
![]() .
.
21、(本小题满分14分)
设函数![]() 、
、![]() R)。
R)。
(1)若![]() ,过两点(0,0)、(
,过两点(0,0)、(![]() ,0)的中点作与
,0)的中点作与![]() 轴垂直的直线,与函数
轴垂直的直线,与函数![]() 的图象交于点
的图象交于点![]() ,求证:函数
,求证:函数![]() 在点P处的切线点为(
在点P处的切线点为(![]() ,0)。
,0)。
(2)若![]() ),且当
),且当![]() 时
时![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
湖南省十校联考理科数学参考答案
一、选择题
1-5ABCBA 6-10 DADAB
二、填空题
11、![]() ; 12、2cosx ; 13、1 ; 14、2 ; 15、
; 12、2cosx ; 13、1 ; 14、2 ; 15、![]() 。
。
三、解答题(本大题共6个小题,共80分)
16.解:(1)∵![]() =(sinB,1-cosB)
, 且与向量
=(sinB,1-cosB)
, 且与向量![]() (2,0)所成角为
(2,0)所成角为![]()
∴![]() ……………………………………………………………………3’
……………………………………………………………………3’
∴tan![]() ……………………6’
……………………6’
(2)由(1)得![]()
………………………………………………8’
∵![]()
∴![]() ……………………………………………………………………10’
……………………………………………………………………10’
∴![]()
当且仅当![]() …………………………………………12’
…………………………………………12’
17、解:(1)当![]() 时的概率为
时的概率为![]() ……………2分
……………2分
当![]() 且
且![]() 时的概率为
时的概率为![]() …………4分
…………4分
(2)![]() ……………………6分
……………………6分
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
因为y的数学期望为![]() ,所以
,所以![]() ………10分
………10分
于是![]() ,
,![]() ………………………12分
………………………12分
18、解:∵平面![]() 平面
平面![]() ,AE⊥EF,∴AE⊥面平面
,AE⊥EF,∴AE⊥面平面![]() ,AE⊥EF,AE⊥BE,又BE⊥EF,故可建立空间坐标系E-xyz。则A(0,0,2),B(2,0,0),G(2,2,0),
,AE⊥EF,AE⊥BE,又BE⊥EF,故可建立空间坐标系E-xyz。则A(0,0,2),B(2,0,0),G(2,2,0),
D(0,2,2),E(0,0,0)
(1)![]() (-2,2,2)
(-2,2,2)![]() (2,2,0)
(2,2,0)
![]() (-2,2,2)
(-2,2,2)![]() (2,2,0)=0,∴
(2,2,0)=0,∴![]() ……4分;
……4分;
(2)∵AD∥面BFC,![]() VA-BFC=
VA-BFC=![]() =
=![]()
![]() 4
4![]() (4-x)
(4-x)![]() x
x
![]() 即
即![]() 时
时![]() 有最大值为
有最大值为![]() 。……8分
。……8分
(3)设平面DBF的法向量为![]() ,∵AE=2, B(2,0,0),D(0,2,2),
,∵AE=2, B(2,0,0),D(0,2,2),
F(0,3,0),∴![]()
![]() (-2,2,2),
(-2,2,2),
则 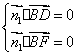 ,即
,即![]() ,
,![]()
取x=3,则y=2,z=1,∴![]() ……11分
……11分
面BCF的一个法向量为![]()
则cos<![]() >=
>=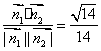 ……13分
……13分
二面角D-BF-C的平面角为π-arccos![]() ……14分。
……14分。
19、解(1)![]() ……………2分
……………2分
![]()
由已知![]() ………………4分
………………4分
![]() ……………5分
……………5分
(2)设过点A的直线为![]()
![]() …9分
…9分
![]() …………11分
…………11分
![]() , 所以
, 所以
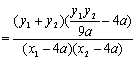 ,由
,由![]() ,得
,得![]() =0 …………14分
=0 …………14分
20、解:(1)∵ ![]() ,a,
,a,![]() ,
,
∴ ![]() ∴
∴  ∴
∴ 
∴ ![]() .
…………4分
.
…………4分
∴ a=2或a=3(a=3时不合题意,舍去). ∴a=2.…………5分
(2)![]() ,
,![]() ,由
,由![]() 可得
可得
![]() . ∴
. ∴ ![]() .
.
∴ b=5 …………8分
(3)由(2)知![]() ,
,![]() , ∴
, ∴ ![]() .
.
∴ ![]() . ∴
. ∴ ![]() ,
,![]() .……10分
.……10分
∵ ![]() ,
,![]() . …………11分
. …………11分
当n≥3时,
![]()
![]()
![]()
![]() .
.
∴ ![]() . 综上得
. 综上得 ![]()
![]() …………14分
…………14分
21、解(1)由已知![]() …………1分
…………1分
![]() …………2分
…………2分
所求,所求切线斜率为![]() …………3分
…………3分
切线方程为![]()
所以,函数y=f (x)过点P的切线过点(b,0) …………4分
(2)因为![]() ,所以
,所以![]() ,
,
![]() …………5分
…………5分
当![]() 时,函数
时,函数![]() 上单调递增,在(
上单调递增,在(![]() ,
,![]() )单调递减,
)单调递减,
在![]() 上单调递增.
上单调递增.
所以,根据题意有 即
即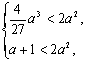
解之得![]() ,结合
,结合![]() ,所以
,所以![]() …………8分
…………8分
当![]() 时,函数
时,函数![]() 单调递增。
…………9分
单调递增。
…………9分
所以,根据题意有![]() …………10分
…………10分
即![]() , 整理得
, 整理得![]() (
(![]() )
)
令![]() ,
,![]()
![]() ,所以“
,所以“![]() ”不等式无解。 …13分
”不等式无解。 …13分
综上可知:![]() 。
…………14分
。
…………14分