高中数学必修一和必修二综合测试B
考号 班级 姓名
一.选择题:(本大题共10小题,每小题5分,共50分。)
1、若![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、函数![]() 的定义域为
的定义域为![]() ,若
,若![]()
![]()
![]() ,
,![]() ,则
,则![]() ( )
( )
A.
![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
 3、如图1,在正四棱柱
3、如图1,在正四棱柱![]() 中,
中,![]() 分别是
分别是![]() ,
,![]() 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )
A.![]() 与
与![]() 垂直 B.
垂直 B.![]() 与
与![]() 垂直
垂直
C.![]() 与
与![]() 异面 D.
异面 D.![]() 与
与![]() 异面
异面
4、.若直线![]() 和直线
和直线![]() 垂直,则
垂直,则![]() 的值为 ( )
的值为 ( )
![]()
5、设![]() 为两条直线,
为两条直线,![]() 为两个平面,下列四个命题中,正确的命题是( )
为两个平面,下列四个命题中,正确的命题是( )
A.若![]() 与
与![]() 所成的角相等,则
所成的角相等,则![]() B.若
B.若![]() ,
,![]() ,
,![]() ,则
,则![]()
C.若![]() ,
,![]() ,
,![]() ,则
,则![]() D.若
D.若![]() ,
,![]() ,
,![]() ,则
,则![]()
6.、函数![]() 的定义域为( )
的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、若圆![]() 的圆心到直线
的圆心到直线![]() 的距离为
的距离为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
8、圆![]() 关于直线
关于直线![]() 对称的圆的方程是( )
对称的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9、若函数![]() 的定义域为
的定义域为![]() , 则下列函数中可能是偶函数的是 ( ).
, 则下列函数中可能是偶函数的是 ( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10、若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() (其中
(其中![]() 为原点),则
为原点),则![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共4个小题,每小题5分,共20分,把答案填在题中的横线上.)
11、方程![]() 的解是
.
的解是
.
12、圆心为![]() 且与直线
且与直线![]() 相切的圆的方程是 .
相切的圆的方程是 .
13、已知两圆![]() 和
和![]() 相交于
相交于![]() 两点,则直线
两点,则直线![]() 的方程是 .
的方程是 .
14.已知函数![]() ,
,![]() 分别由下表给出
分别由下表给出
|
| 1 | 2 | 3 |
|
| 2 | 1 | 1 |
|
| 1 | 2 | 3 |
|
| 3 | 2 | 1 |
则![]() 的值为
的值为
 三、解答题:
三、解答题:
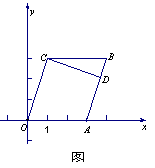
15、(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)如图1,在四边形![]() 中,点C(1,3).(1)求OC所在直线的斜率;
中,点C(1,3).(1)求OC所在直线的斜率;
(2)过点C做CD⊥AB于点D,求CD所在直线的方程.
16、(本小题满分13分)
在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
 (1)求证:EF∥平面CB1D1;
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1
17、(本题满分13分)
已知直线![]() :
:![]() ,
,![]() :
:![]() ,求:
,求:
(1)直线![]() 与
与![]() 的交点
的交点![]() 的坐标;(2)过点
的坐标;(2)过点![]() 且与
且与![]() 垂直的直线方程.
垂直的直线方程.
18、(本小题满分13分)
已知函数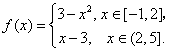
(1)在图5给定的直角坐标系内画出![]() 的图象;
的图象;
 (2)写出
(2)写出![]() 的单调递增区间.
的单调递增区间.
19、(本小题满分13分)
已知圆![]() 的方程为:
的方程为:![]() .
.
(1)试求![]() 的值,使圆
的值,使圆![]() 的面积最小;
的面积最小;
(2)求与满足(1)中条件的圆![]() 相切,且过点
相切,且过点![]() 的直线方程.
的直线方程.
20、(本小题满分14分)
已知圆方程:![]() ,求圆心到直线
,求圆心到直线![]() 的距离的取值范围.
的距离的取值范围.
参考答案
一、DBDCD ACCDA
二、11、![]() 12、
12、![]() 13、
13、![]() 14、
14、![]() 、
、 ![]()
三、
15、(Ⅰ)解: (1)![]() 点O(0,0),点C(1,3),
点O(0,0),点C(1,3),
![]() OC所在直线的斜率为
OC所在直线的斜率为![]() .
.
(2)在![]() 中,
中,![]() ,
,
![]() CD⊥AB,
CD⊥AB,
![]() CD⊥OC.
CD⊥OC.
![]() CD所在直线的斜率为
CD所在直线的斜率为![]() .
.
![]() CD所在直线方程为
CD所在直线方程为![]()
![]() .
.
16、(1)证明:连结BD.
在长方体![]() 中,对角线
中,对角线![]() .
.
又![]() E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
![]() .
.
![]() .
.
又B1D1平面![]() ,
,![]() 平面
平面![]() ,
,
![]() EF∥平面CB1D1.
EF∥平面CB1D1.
(2)![]() 在长方体
在长方体![]() 中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
![]() AA1⊥B1D1.
AA1⊥B1D1.
又![]() 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1,
![]() B1D1⊥平面CAA1C1.
B1D1⊥平面CAA1C1.
又![]() B1D1平面CB1D1,
B1D1平面CB1D1,
![]() 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.
17、(1)解方程组![]() 得
得![]() ,所以交点
,所以交点![]()
(2)![]() 的斜率为3,故所求直线为
的斜率为3,故所求直线为![]()
即为![]()
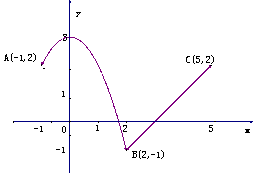 18、解:(1)函数
18、解:(1)函数![]() 的图像如右图所示;
的图像如右图所示;
(2))函数![]() 的单调递增区间为[-1,0]和[2,5]
的单调递增区间为[-1,0]和[2,5]
说明:单调递增区间没有写成闭区间形式,统一扣1分。
19、配方得圆的方程:![]()
(1)当![]() 时,圆的半径有最小值1,此时圆的面积最小。
时,圆的半径有最小值1,此时圆的面积最小。
(2)当![]() 时,圆的方程为
时,圆的方程为![]()
设所求的直线方程为![]()
即![]()
由直线与圆相切,得![]() ,
,![]()
所以切线方程为![]() ,即
,即![]()
又过点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与圆也相切
与圆也相切
所发所求的切线方程为![]() 与
与![]() 。
。
20、解:将圆方程配方得![]() (2分)
(2分)
故满足![]() ,解得
,解得![]() 或
或![]() (6分)
(6分)
由方程得圆心![]() 到直线
到直线![]() 的距离
的距离
![]() ,
,![]() (10分)
(10分)
![]() ,得
,得![]() (14分)
(14分)