数学理科 模拟试卷七
一、选择题:
1. 已知集合M和集合N中含有的元素个数相等,且MUN={a,b,c,d},
则M的不同构成方式有:( )
(A) 3种 (B) 6种
(C) 10种 (D) 11种
2. 已知y=f(x)是定义在R上的奇函数,当x≥0时,![]() ,则f(x)在R
,则f(x)在R
上的解析式是:( )
(A) y=x(x-2) (B) y=x(|x|-2)
(C) y=|x|(x-2) (D) y=|x|(|x|-2)
3. 函数f(x)与![]() 的图象关于直线y=x对称,则函数
的图象关于直线y=x对称,则函数![]() 的
的
递增区间是( )
(A) (-2,2) (B) (0,+∞)
(C) (0,2) (D) (-∞,0)
4. 已知tgα=ctgβ=3![]() ,且
,且![]() ,则a的值是( )
,则a的值是( )
(A) 2
(B)![]() (C) -
(C) -![]() (D) -2
(D) -2
5. 已知不重合的直线a、b和平面M,下面四个命题中,正确的是:( )
a∥b a⊥M
(A) } => b∥M (B) } => b∥a
a∥M b⊥M
a⊥M a∥M
(C) } => b∥M (D) } => b⊥M
a⊥b a⊥b
6. 线段AB与线段MN交于点C,D是线段AB上不同于点C的另一点,则以A、B、C、D、
M、N六个点为顶点可组成不同的三角形( )
(A) 18个 (B) 16个
(C) 15个 (D) 12个
7. 过抛物线y![]() =4x的焦点作直线交抛物线于A(x
=4x的焦点作直线交抛物线于A(x![]() ,y
,y![]() )、B(x
)、B(x![]() ,y
,y![]() )两点,
)两点,
若x![]() +x
+x![]() =6,则|AB|的值为( )
=6,则|AB|的值为( )
(A) 10 (B) 8
(C) 6 (D) 4
8. 若复数1+2i辐角的主值为α,3-4i辐角的主值为β,则2α-β的值为( )
(A) -π
(B) -![]()
(C) π (D)![]()
9. 棱台上,下底面的面积的比为1:4,则它的中截面把它分成上、下两个台体的体积的比
为:( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
10. 已知双曲线的渐近线方程是![]() ,则此双曲线的标准方程是(
)
,则此双曲线的标准方程是(
)
(A) ![]() (B)
(B)
![]()
(C)![]() (k>0)
(D)
(k>0)
(D) ![]() (k≠0)
(k≠0)
11. 不等式![]() >0的解集为( )
>0的解集为( )
(A) {x|x∈R且x≠0} (B) {x|x<-1或x>0}
(C) {x|x<-1} (D) {x|x>0}
12. 三棱锥A-BCD中,E、F分别是AC、BD的中点,若AB=CD=2,![]() ,
,
那么AB和CD所成的角为( )
(A) ![]() (B)
(B)
![]() (C)
(C) ![]() (D)
(D) ![]()
13. 已知函数y=Asin(ωx+φ)+m的最大值是4,最小值是0,最小正周期为![]() ,直线
,直线
![]() 是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
是其图象的一条对称轴,则下面各式中符合条件的解析式是( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D) ![]()
14. 设首项为3,公比为2的等比数列{a![]() }的前n项和为S
}的前n项和为S![]() ,首项为2,公比为3的等比
,首项为2,公比为3的等比
数列{a'![]() }的前n项和为S'
}的前n项和为S'![]() ,则
,则![]() 的值等于( )
的值等于( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D) 2
(D) 2
15. 曲线![]() (x∈[-2,2])与直线y=k(x-2)+4有两个公共点时,
(x∈[-2,2])与直线y=k(x-2)+4有两个公共点时,
实数k的取值范围是( )
(A) ( 0,![]() )
(B) (
)
(B) ( ![]() ,
,![]() )
)
(C) (![]() ,+∞ )
(D) (
,+∞ )
(D) (![]() ,
,![]() ]
]
二、填空题:
16. 计算 ![]() ( )
( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
17. 极坐标系中,圆锥曲线![]() 的左准线方程是:( )
的左准线方程是:( )
(A) ρcosθ=2 (B) ρcosθ=8
(C) ρcosθ=5 (D) ρcosθ=-2
18. 若(sinA-2ctg![]() 展开式中第3项是6,则三角形内角A=( )°.
展开式中第3项是6,则三角形内角A=( )°.
|
19. 如图,正方形ABCD被对角线BD,以及以C为圆心,CB半径的圆弧BD分成了Ⅰ、Ⅱ、 Ⅲ三个封闭部分,现以CB为轴分别将这三个部分旋转一周,得到三个几何体,则这
三个几何体体积之比为V |
20. 不等式![]() >x+1的解集为( )
>x+1的解集为( )
(A) {x|x<-4或x>5} (B) {x|x≤-4或x>5}
(C) {x|-4<x<5} (D) {x|x>5}
三、解答题:
21. 已知等差数列{a![]() }前4项的和等于40,a
}前4项的和等于40,a![]() +a
+a![]() =68,求数列的通项公式及前n项和s
=68,求数列的通项公式及前n项和s![]() .
.
[解答]
22. 已知![]() ,求sin2αsin2β-cos
,求sin2αsin2β-cos![]() (α-β)的值是:( ).
(α-β)的值是:( ).
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
[解答]
23. 设方程x![]() -2x+k=0 的根分别为α、β,且|α-β|=
-2x+k=0 的根分别为α、β,且|α-β|=![]() ,求实数k的值是:( )
,求实数k的值是:( )
(A) k=1或k=3 (B) k=-1或k=3
(C) k=-1或k=-3 (D) k=1或k=-3.
[解答]
|
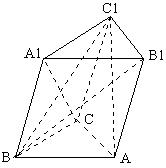
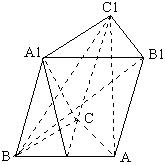
24. 已知斜三棱柱ABC-A 面所成的角为 |
(1) 判定B![]() C与C
C与C![]() A是否垂直,并证明你的结论。
A是否垂直,并证明你的结论。
[解答]
|
(2) 求四棱锥B-ACC |
[解答]
25. 某商店以每件20元的价格购进货物,然后以每件30元的价格售出,每月售出400件,
试销中发现,若每件售价提高1元,则每月少售20件,问每件售价应为( )
元,利润最大。
[解答]
26. 已知椭圆![]() (a>b>0)的长轴两端点为A、B,
(a>b>0)的长轴两端点为A、B,
若椭圆C上存在点Q,使∠AQB=120°,求椭圆C的离心率e的取值范围是( )。
(A) e∈[![]() ,1]
(B) e∈[
,1]
(B) e∈[![]() ,1]
,1]
(C) e∈[![]() ,1]
(C) e∈[
,1]
(C) e∈[![]() ,1]
,1]
[解答]
参 考 答 案
一、
1. D 2. B 3. C 4. B 5. B
6. C 7. B 8. A 9. A 10. D
11. C 12. A 13. B 14. C 15. D
二、填空题:
16. C 17. D 18. 120° 19. 1:1:1 20. B
三、
21. [解答] a![]() +a
+a![]() +a
+a![]() +a
+a![]() =40 a
=40 a![]() +a
+a![]() =68
=68
4a![]() +6d=40,
+6d=40,
即
解之,得a![]() =1, d=6. a
=1, d=6. a![]() =1+(n-1)×6=6n-5.
=1+(n-1)×6=6n-5.
2a![]() +11d=68.
+11d=68.
![]() .
.
22. C
[解答]
原式= sin2αsin2β-cos![]() (α-β)
(α-β)
![]() (cos(2α+2β)-cos(2α-2β)]-
(cos(2α+2β)-cos(2α-2β)]-![]() [1+cos*(2α-2β))
[1+cos*(2α-2β))
= -![]() cos(2α+2β)-
cos(2α+2β)-![]() =-cos
=-cos![]() (α+β)
(α+β)
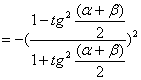
 .
.
23. B
[解答] ∵ |α-β|=![]() . ∴ |α-β|
. ∴ |α-β|![]() =8,
=8,
即 |(α+β) ![]() -4αβ|=8 又α+β=2, αβ=k,
-4αβ|=8 又α+β=2, αβ=k,
∴|4-4k|=8. 1-k=±2. ∴ k=-1或k=3.
24.(1) [解答] 作B![]() D⊥AB,交AB于D,连结CD,
D⊥AB,交AB于D,连结CD,
| ∵平面ABB 由已知得∠B ∴BD=B |
∵CD∩B![]() D=D. ∴AB⊥平面B
D=D. ∴AB⊥平面B![]() DC. ∴
AB⊥B
DC. ∴
AB⊥B![]() C.
C.
又∵B![]() BCC
BCC![]() 是菱形。 ∴两对角线B
是菱形。 ∴两对角线B![]() C⊥BC
C⊥BC![]()
∴B![]() C⊥平面ABC
C⊥平面ABC![]() ∵BC
∵BC![]() ∩AB=B. 又AC
∩AB=B. 又AC![]() 平面ABC
平面ABC![]() . ∴B
. ∴B![]() C⊥C
C⊥C![]() A.
A.
(2) [解答]
![]() .
.
|
又由(1)知B ∴ 又 |
∴![]() .
.
25. ( 35 )
[解答] 设每件售价应提高x元,每月利润为y元,
则:y=(30-20+x)(400-20x)=20(10+x)(20-x).
∵10+x>0,20-x>0, ∴y≤20×[![]() =4500
=4500
当10+x=20-x,即x=5时,y取得最大值。
即每件售价为35元时,利润最大。
26. D
[解答] 设A(-a,0),B(a,0).设Q(x,y).由椭圆对称性,
不妨设Q点在X轴上方,即y>0. ∴![]() ,
,![]() .
.
由tg∠AQB=tg120°=![]() ,得
,得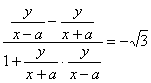 .
.
∴![]() .①
.①
又∵点Q在椭圆C上. ∴![]() . ②
. ②
由①②消去x得:![]() .
.
∴![]() .
.
∵y≠0. (当y=0时,Q点与A或B重合,故舍去) ∴![]() .
.
∵椭圆y≤b. ∴ ![]() ≤b.
≤b.
∴ ![]() ≤c
≤c![]() 将上式两边平方得4a
将上式两边平方得4a![]() b
b![]() ≤3c
≤3c![]() ,即4a
,即4a![]() (a
(a![]() -c
-c![]() )≤3c
)≤3c![]()
∴3c![]() +4a
+4a![]() c
c![]() -4a
-4a![]() ≥0. 即
≥0. 即![]() ≥0.
≥0.
∵![]() . ∴3e
. ∴3e![]() +4e
+4e![]() -4≥0. ∴3e
-4≥0. ∴3e![]() -2≥0
-2≥0
∴e![]() ≥[
≥[![]() ]. ∴e∈[
]. ∴e∈[![]() ,1]
,1]