国家命题研究中心2005年高考数学信息题（密卷）
说明：题目顺序有意打乱不要随意发布。仅作参考用。请在下载24小时内删除。违者责任自负。谢谢合作
一. 选择题：( 本大题共12小题，每小题5分，共60分 )
1.
直线 
的倾斜角是
（C）
A. 
B. 
C.
D. 
答：斜率为
，倾斜角为钝角.
2. 
的近似值（精确到小数后第三位）为
（A）
A. 726.089 B. 724.089 C. 726.098 D. 726.908
答：
3.
在
中. 若 
，则 
（C）
A. 
B. 
C.
D.
答：
4. 设
为平面上以 
为顶点的三角形区域( 包括边界 ),则
的最大值和最小值分别为 （A）
A. 14 , -18 B. -14 , -18 C. 18 , 14 D. 18 , -14
答：画出示意图，易知：当动直线过
时，
取最大值；当动直线过
时，取最小值.
5. 给定集合
，定义 
.若 
，则
集合 
中的所有元素之和为
（A）
A. 15 B. 14 C. 27 D. -14
答A※B={3，2，1，4，5}，元素和为15．
6． 已知函数
在
上是减函数，则实数a的取值范围为 （D）
A. （5，+∞） B. （3，+∞） C. （-∞，3） D. 
答
定义域为
．而函数
在
时为增函数，故
的单调减区间为
，从而 
．
7． 设函数
，若
，则下列不等式必定成立的是 （B）
A．
B． 
C． 
D． 
答
易知
，且当x∈
时，
为增函数．又由，得
，故 
，于是．
8． 已知等比数列
的首项为8，
是其前n项的和，某同学经计算得S2=20，S3=36，S4=65，后来该同学发现了其中一个数算错了，则该数为 （C）
A． S1 B． S2 C． S3 D． S4
答
显然S1是正确的．假设后三个数均未算错，则a1=8，a2=12，a3=16，a4=29，可知a22≠a1a3，故S2、S3中必有一个数算错了．若S2算错了，则a4=29=a1q3，
，显然S3=36≠8(1+q+q2)，矛盾．故只可能是S3算错了，此时由a2=12得
，a3=18，a4=27，S4=S2+18+27=65，满足题设．
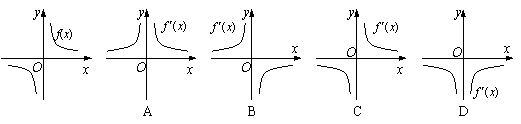9． 函数
的图象如图所示，则导函数
的图象大致是 （D）
答
由
的图象及
的意义知，在x＞0时，为单调递增函数且
＜0；在x＜0时，为单调递减函数且＜0．
10．我们把离心率为黄金比
的椭圆称为“优美椭圆”．设
(a＞b＞0)为“优美椭圆”，F、A分别是它的左焦点和右顶点，B是它短轴的一个端点，则∠ABF等于
（C）
A．60° B．75° C．90° D．120°
答
依题意， 
， 
，故△ABF为直角三角形
且∠ABF为直角，答案选C．
11．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为y= -x2，值域为{-1，-9}的“同族函数”共有 （C）
A．7个 B．8个 C．9个 D．10个
答 定义域中可能有的元素为1，-1，3，-3，而且在1与 -1，3与 -3中各至少有一个在定义域内．
当定义域中只有2个元素时，可有{1，3}，{1，-3}与{-1，3}，{-1，-3}，共4种可能；
当定义域中含有3个元素时，可能
=4种可能；
当定义域中含有4个元素时，只有1种可能． 4+4+1=9．
12．半径为4的球面上有A、B、C、D四点，且满足
，
，
，则
的最大值为（
为三角形的面积） （C）
A．8 B．16 C．32 D．64
答 易知AB，AC，AD两两互相垂直，进而AB2+AC2+AD2=(2r)2=64．
S△ABC+S△ACD+S△ADB=
≤
=
．
二、填空题：（本大题共4小题，每小题4分，共16分．）
13、某人要买房，若要第
层楼，则因上下楼造成的不满意度为，但随楼层升高，环境的不满意度降低。设要第层楼时，环境的不满意度为
，则此人应选第___6___层楼.
14、已知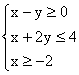
，则
的最小值为_____2____
15．为等差数列的前n项和，若
，则
= 4 ．
答
由，即 
，得
．
，
．故=4．
16．若
，且
，则
的值是 11 ．
答
由
≥10，得
lg()≥lg10=1，即(lgx)2+(lgy)2≥1= (lgx+lgy)2，于是2lgxlgy≤0，从而lgx与lgy中必有一个为0，即x与y中必有一个为1，因而另一个为10．
三、解答题：（本大题共6小题，共74分．）
17．（本小题满分12分）
已知 
，
．
（1）求
的值； （2）求
的值．
解 （1）将已知两式平方相加得
，故
．………7分
（2）∵
，………………………………………………9分
∴
． ∴
．
…………………………………………12分
18．（本小题满分12分）
某学生语、数、英三科考试成绩，在一次考试中排名全班第一的概率：语文为0.9，数学为0.8，英语为0.85，问一次考试中：
（1）三科成绩均未获得第一名的概率是多少？
（2）恰有一科成绩未获得第一名的概率是多少？
解 分别记该生语、数、英考试成绩排名全班第一的事件为A、B、C，则P(A)=0.9，P(B)=0.8，P(C)=0.85．…………………………………2分
(1)
=[1-P(A)]·[1-P(B)]·[1-P(C)]
=(1-0.9)×(1-0.8)×(1-0.85)
=0.003
答：三科成绩均未获得第一名的概率是0.003．……………………………………7分
(2)P(
)
= P(
=
=[1-P(A)]·P(B)·P(C)+P(A)·[1-P(B)]·P(C)+P(A)·P(B)·[1-P(C)]
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85) =0.329．
答：恰有一科成绩未获得第一名的概率是0.329．…………………………………12分
19．（本小题满分12分）
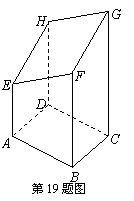如图是表示以AB=4，BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体，其中四边形EFGH为截面．已知AE=5，BF=8，CG=12．
（Ⅰ）作出截面EFGH与底面ABCD的交线l；
（Ⅱ）截面四边形EFGH是否为菱形？并证明你的结论；
（Ⅲ）求DH的长；
（Ⅳ）求截面EFGH与底面ABCD所成锐角的余弦值．
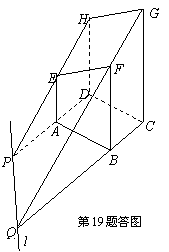
解 （Ⅰ）如图，作HE与DA的交点P，作GF与CB的交点Q，连PQ得直线l，它便是所求作．………………3分
（Ⅱ）截面EFGH为菱形．
因平面ABFE∥平面DCGH，且平面EFGH分别截平面ABFE与平面DCGH得直线EF与GH，故EF∥GH．
同理，FG∥EH，故四边形EFGH为平行四边形．
又EF2=AB2+(BF-AE)2=25，FG2=BC2+(CG-BF)2=25，于是 EF=FG=5，
故 四边形EFGH为菱形．…………………………6分
（Ⅲ）由AE+CG=BF+DH，得 DH=9． …………8分
（Ⅳ）FH2=BD2+(DH-BF)2=26，
EG2=AC2+(CG-AE)2=74，
故菱形EFGH的面积为
SEFGH =
．
又SABCD =
，
由面积射影定理得，所求锐角的余弦为
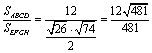．…………………12分
20．（本小题满分12分）
是以
为焦点的双曲线C：
（a＞0，b＞0）上的一点，已知
，
．
（1）试求双曲线的离心率
；
（2）过点P作直线分别与双曲线两渐近线相交于P1、P2两点，当
，
= 0，求双曲线的方程．
解 （1）∵
，
， ∴
，
．
∵
=0，∴(4a)2+(2a)2=(2c)2，∴
．………………………………4分
（2）由（1）知，双曲线的方程可设为
，渐近线方程为
．…5分
设P1(x1，2x1)，P2(x2，-2x2)，P(x，y)．
∵
，∴
． ∵
，∴
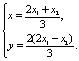………8分
∵点P在双曲线上，∴
．
化简得，
．∴
．∴ 
． ∴双曲线的方程为
．………12分
21．（本小题满分12分）
等比数列的首项为
，公比
．
（1）设
表示该数列的前n项的积，求的表达式；
（2）当n取何值时，有最大值．
解 （1）
，
．………………………………4分
（2）∵
，
∴当n≤10时，＞1，∴ f(11)
＞ f(10)
＞…＞ f(1) ；……………6分
当n≥11时，
＜1，∴ f(11)
＞ f(12)
＞…．………………………8分
∵
，∴
的最大值为
或
中的最大者．10分
∵
，
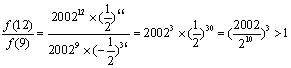∴ 当n=12时，有最大值为
．……………………………12分
22．（本小题满分14分）
设是定义在[-1，1]上的偶函数，
的图象与的图象关于直线
对称，且当
x∈[ 2，3 ] 时，
222233．
（1）求的解析式；
（2）若在
上为增函数，求
的取值范围；
（3）是否存在正整数，使的图象的最高点落在直线
上？若存在，求出的值；若不存在，请说明理由．
解： （1）当x∈[-1，0]时，2-x∈[2，3]，f(x)=g(2-x)=
-2ax+4x3；当x∈时，f(x)=f(-x)=2ax-4x3，
∴
…………………………………………………4分
（2）由题设知，
＞0对x∈恒成立，即2a-12x2＞0对x∈恒成立，于是，a＞6x2，从而a＞(6x2)max=6．…………………………………………………8分
（3）因f(x)为偶函数，故只需研究函数f(x)=2ax-4x3在x∈的最大值．
令=2a-12x2=0，得
．…………10分 若
∈
，即0＜a≤6，则
，
故此时不存在符合题意的；
若＞1，即a＞6，则在上为增函数，于是
．
令2a-4=12，故a=8． 综上，存在a = 8满足题设．……………………………14分