霍市一中三月份模拟考试
数 学 (文科)
一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的.每题5分
1、已知集合
，若
，则
等于（ ）
A、1 B、2 C、1或2 D、1或2.5
2、若
，则
=（ ）
A、
B、
C、
D、
3、函数
的定义域为 （ ）
A、
B、
C、（1，2） D、
4、已知
，若
，则的值等于（ ）
A、
B、
C、
D、
5、已知斜率为
的直线
被圆
所截，截得的弦
的长等于（ ）
A、4
B、2
C、
D、
6、已知
是直线，
是平面，给出下列命题：①
，则
；②
，
，则
；③
，则
；④
，则
。其中错误的命题的序号是（ ）
A、① B、② C、③ D、④
7、若向量
，则
与
一定满足（ ）
A、与的夹角等于
B、
C、
D、
8、圆
与
轴交于
两点，圆心为
，若
，则
的值为（ ）
A、8
B、3
C、
D、
9、已知等比数列
的前
项和
，则
等于 （ ）
A、
B、
C、
D、
10、点
是直线
上的动点，则代数式
有（ ）
A、最大值8 B、最小值8 C、最小值6 D、最大值6
11、如果
，那么在①
；②
；③
；④
中，正确的有（ ）
A、1个 B、2个 C、3个 D、4个
12、弹子跳棋共有60颗大小相同的球形弹子，现在棋盘上将它叠成正四面体形球垛，使剩下的弹子尽可能的少，那么剩余的弹子共有（ ）
A、0颗 B、4颗 C、5颗 D、11颗
二、填空题：把答案填在题中横线上。每题4分。
13、已知函数
，则
=
.
14、从某高校的8名优秀毕业生中选派5名支援中国西部开发建设，某人必须被选派的种数是 .
15、设抛物线
的一条弦以
为中点，则该弦所在直线的斜率为
.
16、已知两异面直线所成的角为
，直线
与所成的角都是
，则的取值范围是 .
三、解答题：解答应写出文字说明、证明过程或演算步骤。
17、(本小题满分12分)
已知函数
（1）求
的最小正周期；
（2）求的单调递减区间；
18、（本体满分12分）某种装置开关闭和后，便有红绿灯闪烁，设第一次闪烁出现红、绿灯的概率都是
，从第二次闪烁起，前次出现红灯后接着出现红灯的概率
，接着出现绿灯的概率
；同样，前次出现绿灯后接着出现红灯的概率是
，出现绿灯的概率是
。
求（1）第二出现红灯的概率。
（2）三次闪烁，红灯出现一次，绿灯出现两次的概率。
（3）三次闪烁红绿灯交替出现的概率。
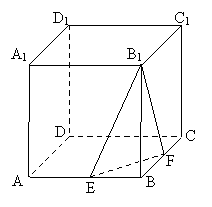19、(本小题满分12分)如图所示，在棱长为的正方体
中，
分别是棱与
的中点.
（1）求二面角
的大小；
（2）求点
到平面
的距离。
20、（本题满分12分）已知函数
在
处有极值，曲线
在
处的切线平行于直线
试求函数的极大值与极小值的差。
21．(本小题满分14分)
已知f(x)在(－1，1)上有定义，f(
)＝－1，且满足x，y∈(－1，1)有f(x)＋f(y)＝f(
)
⑴证明：f(x)在(－1，1)上为奇函数；
⑵对数列x1＝，xn＋1＝
，求f(xn);
⑶求证
22．（本小题满分12分）
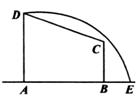如图所示，在直角梯形ABCD中，AD＝3，AB＝4，BC＝，曲线段DE上任一点到A、B两点的距离之和都相等．
（1）建立适当的直角坐标系，求曲线段DE的方程；
（2）过C能否作一条直线与曲线段DE相交，且所
得弦以C为中点，如果能，求该弦所在的直线
的方程；若不能，说明理由．
参考答案
一、选择题：CBDDC BCDDC BB
二、填空题：13、
14、35 15、2
16、
三、解答题：17、解：（Ⅰ）由
由
∴函数的最小正周期T=
（Ⅱ）由
∴的单调递减区间是
.
。18、（1）×+×
=
（2）××+××+××=
（3）××+××=
19、（1）作
于H，连结EH，则EB⊥面BCC1B知EH⊥B1F，于是∠EHB是二面角
的平面角，在Rt△BB1F中，
∴二面角的大小为
（2）因为
，由
知到面的距离等于
到面DEF的距离，即D到B1EF的距离为。
20、解：
，由于在处有极值，∴
即
①又 ∵处的切线平行于，∴
即
②
解①②得
，∴
令
，得
，
由于在
附近，
左正，右负；而在附近，左负，右正，所以
是函数的极大值，
是函数的极小值，于是
，故函数的极大值与极小值的差为4。
21．(Ⅰ)证明：令x＝y＝0，∴2f(0)＝f(0)，∴f(0)＝0
令y＝－x，则f(x)＋f(－x)＝f(0)＝0
∴f(x)＋f(－x)＝0 ∴f(－x)＝－f(x)
∴f(x)为奇函数 4分
(Ⅱ)解：f(x1)＝f()＝－1，f(xn＋1)＝f()＝f(
)＝f(xn)＋f(xn)＝2f(xn)
∴
＝2即{f(xn)}是以－1为首项，2为公比的等比数列
∴f(xn)＝－2n－1
(Ⅲ)解：
而
∴
22．解：（1）以直线AB为x轴，线段AB的中点为原点建立直角坐标系，则A（－2，0），B（2，0），C（2， ），D（－2，3）．依题意，曲线段DE是以A、B为焦点的椭圆的一部分．
（2）设这样的弦存在，其方程
得
设弦的端点为M（x1，y1），N（x2，y2），则由
∴弦MN所在直线方程为
验证得知，这时
适合条件．
故这样的直线存在，其方程为