高三数学文科复习作业（5）
班级 姓名 座号
1、设
、
是两个非空集合，定义：
.若
，则
中元素的个数是 （ ）
A．3 B．4 C．7 D．12
2、图中的每个开关都有闭合与不闭合两种可能,电路从
到接通的情况共有（ ）种．
A．30 B．24
C．16 D．12
3、已知向量
夹角为
若
，则
的值为（ ）
A．
B．
C．
D．
4、双曲线
的一条准线被它的两条渐近线所截得线段长度恰好为它的一个焦点
到一条渐近线的距离，则该双曲线的离心率是 （ ）
A．3 B．2
C．
D．
5、若一个圆的圆心在抛物线y2=4x的焦点处，且此圆与直线x+y+1=0相切，则这个圆的方程是 （ ）
A．x2+y2－2x－1=0 B．x2+y2+2x+1=0
C．x2+y2－2y+1=0 D．x2+y2+2y+1=0
6、．某城市对一种售价为每件160元的电子产品征收附加税，税率为
（即每销售100元征税
元），若年销售量为30－
万件，要使附加税不少于128万元，则R的取值范围是 （ ）
A．[4，8] B．[6，10] C．[4%，8%] D．[6%，10%]
7、已知
的展开式中所有二项式系数的和为512，则展开式中
项的系数为_____．
8、在
中，有命题①
；②
；③若
，则为等腰三角形；④若
，则为锐角三角形.上述命题正确的是_____________
|
；（Ⅱ）求证：
平面PAD；
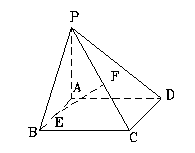
（Ⅲ）当平面PCD与平面ABCD成多大角时，直线
平面PCD？
10、已知函数
满足
，且
．
（1）当
时，求的表达式；
（2）设
,求证：
作业（5）答案：1、D2、C3、C4、B5、A6、A 7、-84 8、②，③
9.证（Ⅰ）∵PA^底面ABCD
AD是PD在平面ABCD内的射影。
∵CDÌ平面ABCD，且CD^AD，
故CD^PD ．………………...…4分
（Ⅱ）取CD中点G，连结EG、FG
∵E、F分别是AB、PC的中点，\EG//AD，FG//PD，
\平面EFG//平面PAD，\EF//平面PAD． ……………..……8分
（Ⅲ）当平面PCD与平面ABCD成45°角时，直线EF^平面PCD。
证明：G为CD中点，则EG^CD，由（1）知FG^CD，
故ÐEGF为平面PCD 与平面ABCD所成二面角的平面角，即ÐEGF=45°，
从而得ÐADP=45°， AD=AP。
由，得PE=CE。
又F是PC的中点，\EF^PC。
由CD^EG，CD^FG，得CD^平面EFG，CD^EF，即EF^CD，
故EF^平面PCD． …………..……………….………….12分
10.（1）由已知得f (n)=f (n -1) f
(1)=
f (n-1)=
f (n-2)=…=
；….5分
（2）由（1）知
，设
，则用错位相减法求和得：
；……12分