高三文科复习作业(11)
班级 姓名 座号
1、要得到函数
的图象，只需将函数
的图象做以下平移（ ）
A．按向量
平移 B．按向量
平移
C．按向量
平移 D．按向量
平移
2、已知
的取值范围是
（ ）
A．
B．
C．
D．
3、箱子里有5个黑球，4个白球，每次随机取出一个球，若取出黑球，则放回箱中，重新取球，若取出白球，则停止取球，那么在第4次取球之后停止的概率 （ ）
A．
B．
C．
D．
4、n个连续自然数按规律排成下表： 0 3→4 7→8 11→…
↓ ↑ ↓ ↑ ↓ ↑
根据规律，从2002到2004，箭头的方向 1→2 5→6 9→10依次为 （ ）
A．↓→ B．↑→ C．→↑ D．→↓
5、设f(x)表示－x+6和－2x2+4x+6中较小者，则f(x)的最大值为 .
6、经过函数
图象的任意一点的切线的倾斜角的取值范围是
7、由动点P向圆
PA、PB，切点分别为A、B，∠APB=60°，则动点P的轨迹方程是
8、下面有四个命题：
①若
、
为一平面内两非零向量，则
的充要条件；
②一平面内两条曲线的方程分别是
，它们的交点是
，则方程
的曲线经过点P；
③经过一定点且和一条已知直线垂直的所有直线都在同一平面内；
④若函数
的图象关于直线
对称，则
为偶函数.
其中真命题的序号是 （把符合要求的命题序号都填上）.
9、在△ABC中，已知
（1）求证：a、b、c成等差数列；
（2）求角B的取值范围.
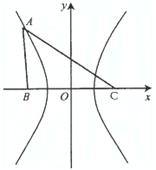
10、如图，在面积为18的△ABC中，AB=5，双曲线E过点A，且以B、C为焦点，已知
（Ⅰ）建立适当的坐标系，求双曲线E的方程；
（Ⅱ）是否存在过点D（1，1）的直线l，使l与双曲线E交于不同的两点M、N，且
如果存在，求出直线l的方程；如果不存在，请说明理由.
|
作业（11）答案：1、B 2、A 3、B 4、B
5、6 6、
7、
8、．①②③④
9、解：由条件得
a、b、c成等差数列
（2）
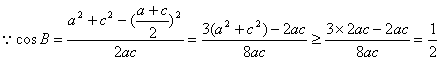
内是减函数，
.
10、解：（Ⅰ）以BC所在直线为x轴，线段BC的中点O为原点，线段BC的中垂线为y轴建立坐标系如图.
设
…………2分
|
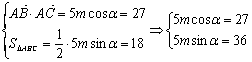
两式平方相加，得m=9. ………………2分
又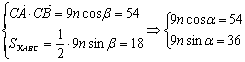
两式平方相加，得
………………2分
设双曲线的方程为 
由双曲线的定义，
有2a=AC－AB=m－5=4，即a=2. 又2c=
，即
∴b2=c2－a2=9. ∴双曲线E的方程为
……2分
（Ⅱ）假设存在满足条件的直线l，使l与双曲线E交于不同两点M、N，
并设
由
知点D是线段MN的中点，
∴
…………1分 由于点M、N都在双曲线E上，
∴
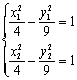. 将两式相减，得
此时直线l的方程为 
……3分
但由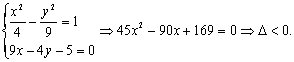
∴不存在满足条件的直线l. ………………2分