泉州市06届高三四校联考数学试卷(文科)(2006.1)
(试卷满分150分,考试时间120分钟)
第I卷 (选择题 共60分)
一、 选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,将正确答案填入答题卡的表格中.)
1、cos600°= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、已知函数![]() = ( )
= ( )
A.b B.-b C.![]() D.-
D.-![]()
|
4、一元二次方程![]() 有一个正实数根和一个负实数根的充分不必要条件是 ( )
有一个正实数根和一个负实数根的充分不必要条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、一所中学有高一、高二、高三学生共1600名,其中高三学生400名.如果通过分层抽样的方法从全体高中学生中抽取一个160人的样本,那么应当从高三年级的学生中抽取的人数是 ( )
A.20 B.40 C.60 D.80
6. 若P![]() 为圆
为圆![]() 的弦AB的中点, 则直线AB的方程是 ( )
的弦AB的中点, 则直线AB的方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
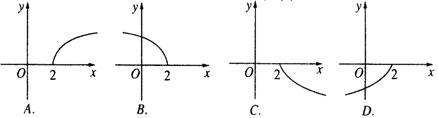
7、若把函数![]() 的图象按向量
的图象按向量![]() 平移后,得到函数
平移后,得到函数![]() 的图象,则原图象的函数解析式可以为 ( )
的图象,则原图象的函数解析式可以为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8、已知抛物线的顶点为原点,
焦点在y轴上, 抛物线上点![]() 到焦点的距离为4, 则m的值为
( )
到焦点的距离为4, 则m的值为
( )
A.4 B.-2 C.4或-4 D.2或-2
9、已知奇函数![]() 的定义域为
的定义域为![]() ,且对任意正实数
,且对任意正实数![]() ,恒有
,恒有 ![]() ,则一定有( )
,则一定有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10、若双曲线![]() 和椭圆
和椭圆![]() 的离心率互为倒数,那么以a,b,m为边长的三角形是 ( )
的离心率互为倒数,那么以a,b,m为边长的三角形是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
11、已知平面上直线![]() 的方向向量
的方向向量![]() =
=![]() ,点O(0,0)和A(1,-2)在
,点O(0,0)和A(1,-2)在![]() 上的射影分别是
上的射影分别是![]() 和
和![]() ,则
,则![]() ,其中λ= ( )
,其中λ= ( )
A.![]() B.-
B.-![]() C.2 D. -2
C.2 D. -2
12、离心率为黄金比![]() 的椭圆称为“优美椭圆”. 设
的椭圆称为“优美椭圆”. 设![]()
![]() 是优美椭圆,F、A分别是它的左焦点和右顶点,B是它的短轴的一个端点,则
是优美椭圆,F、A分别是它的左焦点和右顶点,B是它的短轴的一个端点,则![]() 等于
( )
等于
( )
A. 60° B. 75° C. 90° D. 120°
第II卷 (非选择题 共90分)
二、 填空题:(本大题共4小题,每小题4分,共16分。将正确答案填入答题卡中。)
13、若曲线![]() 在点P处的切线平行于直线
在点P处的切线平行于直线![]() , 则点P的坐标为
.
, 则点P的坐标为
.
14、![]() 的值是
.
的值是
.
 15、若双曲线
15、若双曲线![]() 的焦点到相应于该焦点的准线的距离是2,则k= .
的焦点到相应于该焦点的准线的距离是2,则k= .
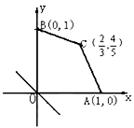
16、给出平面区域如图所示, 目标函数为: ![]() 若当且仅当
若当且仅当![]() 时, 目标函数t取最小值, 则实数a的取值范围是
.
时, 目标函数t取最小值, 则实数a的取值范围是
.
三、解答题:(本大题共6小题,共74分。在答题卡中解答,解答应写出文字说明,证明过程或演算步骤)
17. (本小题满分12分)已知函数![]() 在定义域(-1,1)上是减函数,且
在定义域(-1,1)上是减函数,且
![]()
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)解不等式![]()
18. (本小题满分12分)已知等差数列![]() 的首项
的首项![]() ,且公差d>0,第二项、第五项、第十四项分别是等比数列
,且公差d>0,第二项、第五项、第十四项分别是等比数列![]() 的第二项、第三项、第四项.
的第二项、第三项、第四项.
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)设数列![]() 对任意自然数n均有
对任意自然数n均有![]() 成立,求
成立,求![]() 的值.
的值.
19.(本小题满分12分)已知△ABC内接于单位圆,且(1+tanA)(1+tanB)=2,
(1) 求证:内角C为定值;
(2) 求△ABC面积的最大值.
20.(本小题满分12分)已知![]() 为抛物线
为抛物线![]() 上任意一点, 直线
上任意一点, 直线![]() 为过点A的切线, 设直线
为过点A的切线, 设直线![]() 交y轴于点B. P
交y轴于点B. P![]()
![]() , 且
, 且![]()
![]() .
.
(1) 当A点运动时, 求点P的轨迹方程;
(2) 求点![]() 到动直线
到动直线![]() 的最短距离, 并求此时
的最短距离, 并求此时![]() 的方程.
的方程.
21.(本小题满分12分)已知![]() 是定义在实数集R上的函数,其图象与x轴相交于A,B,C三点,若B点坐标为(2,0),且
是定义在实数集R上的函数,其图象与x轴相交于A,B,C三点,若B点坐标为(2,0),且![]() 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(Ⅰ)求c的值,写出极值点横坐标的取值范围(不需要证明);
(Ⅱ)在函数![]() 的图象上是否存在一点M(
的图象上是否存在一点M(![]() ),使曲线
),使曲线![]() 在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由.
在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由.
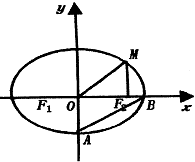 22.(本小题满分14分)如图,
22.(本小题满分14分)如图,![]() 分别是椭圆
分别是椭圆![]() 的左右焦点,M为椭圆上一点,
的左右焦点,M为椭圆上一点,![]() 垂直于
垂直于![]() 轴,且OM与椭圆长轴和短轴端点的连线AB平行,
轴,且OM与椭圆长轴和短轴端点的连线AB平行,
(Ⅰ)求椭圆的离心率;
(Ⅱ)若G为椭圆上不同于长轴端点任一点, 求![]() 取值范围;
取值范围;
(Ⅲ)过![]() 且与OM垂直的直线交椭圆于P,Q. 若
且与OM垂直的直线交椭圆于P,Q. 若![]() ,求椭圆的方程.
,求椭圆的方程.
泉州市06届高三四校联考数学试卷(文科)(2006.1)
参考答案:
一、 选择题:ABCC BCAC DBDC
二、 填空题: 13、![]() ; 14、-
; 14、-![]() ; 15、; 6
; 15、; 6
16、![]()
三、解答题:
17.本题考查函数的基本知识和解不等式的知识.
解:(Ⅰ)由已知得: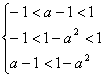
![]()
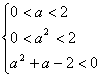
![]()
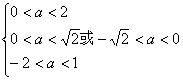
![]()
![]() .
…………………………… 6/
.
…………………………… 6/
(Ⅱ)由(Ⅰ)得![]() ,
,
∴不等式![]()
![]()
![]()
![]()
![]()
![]()
![]() …………………………… 10/
…………………………… 10/
则 原不等式的解集为![]() …………………………… 12/
…………………………… 12/
18. 本题考查等差数列、等比数列的基本知识及数列通项、数列求和等知识.
解:(1)由题意得:![]() ,解得:d=2,
,解得:d=2,
所以![]() ,易得
,易得![]() .
…………………… 5/
.
…………………… 5/
(2)由题意得:![]() ,所以
,所以![]() ,………………… 8/
,………………… 8/
![]()
所以由错位相减法得
![]() …………… 12/
…………… 12/
19. 本题考查正切和角公式,正弦的和(差)角公式,三角形内角和定理、正弦定理,三角函数最值等知识.
(1) 证明:由(1+tanA)(1+tanB)=2![]() tanA+tanB=1-tanAtanB
tanA+tanB=1-tanAtanB
![]() tan(A+B)=1.
…………………… 3/
tan(A+B)=1.
…………………… 3/
∵A、B为△ABC内角, ∴A+B=![]() . 则 C=
. 则 C=![]() (定值). …… 6/
(定值). …… 6/
(2) 解:已知△ABC内接于单位圆, ∴△ABC外接圆半径R=1.
∴由正弦定理得:![]() ,
,![]() ,
,![]() .…… 8/
.…… 8/
则△ABC面积S=![]() =
=![]() =
=![]()
=![]() =
=![]()
=![]() =
=![]() …… 10/
…… 10/
∵ 0<B<![]() , ∴
, ∴![]() .
.
故 当![]() 时,△ABC面积S的最大值为
时,△ABC面积S的最大值为![]() .
…………………… 12/
.
…………………… 12/
20.本题考查求抛物线的切线、求轨迹、点到直线的距离、求最值等知识.
解: (1)设![]() , 因为
, 因为![]() ,
………………………… 1/
,
………………………… 1/
所以过点A的切线方程为![]() ………………………… 2/
………………………… 2/
令![]() , 则
, 则![]() , B点坐标为
, B点坐标为![]() . ………………………… 3/
. ………………………… 3/
又![]() , ∴
, ∴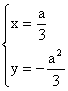 消去a, 得
消去a, 得![]() ………………………… 6/
………………………… 6/
(2)设C到l的距离为d, 则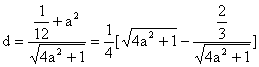 ………… 8/
………… 8/
设![]() , 则
, 则![]() 为t的增函数 …………………… 10/
为t的增函数 …………………… 10/
∴![]() ,此时a=0 .
………………………… 11/
,此时a=0 .
………………………… 11/
故C到l的最短距离为![]() , 此时l的方程为
, 此时l的方程为![]() ……………………… 12/
……………………… 12/
21. 本题考查导数与函数极值、函数单调性,导数的几何意义等知识,及分析问题和解决问题的能力.
解:(Ⅰ)∵![]() 在[-1,0]与[0,2]上有相反的单调性,
在[-1,0]与[0,2]上有相反的单调性,
∴![]() ……………………… 2/
……………………… 2/
又∵![]() 在 [0,2] 与[4,5]上有相反的单调性,
在 [0,2] 与[4,5]上有相反的单调性,
∴极值点横坐标的取值范围![]() ……………………… 4/
……………………… 4/
(Ⅱ)令![]()
∴ 函数![]() 的极值点为
的极值点为![]() ……………………… 6/
……………………… 6/
根据(Ⅰ)得,![]() ∴
∴![]() ……………… 8/
……………… 8/
假设存在满足条件的点M![]() ,
,
令![]() …………①
…………①
方程①的![]()
∴方程①没有实数根. ∴不存在满足条件的M点. ………………… 12/
22. 本题考查椭圆的知识,余弦定理,均值不等式求最值等知识,及分析问题和解决问题的能力.
解:(Ⅰ)由已知![]() , ∵
, ∵![]()
∴![]() , ∴
, ∴![]() ,
,![]() ……………………… 3/
……………………… 3/
(Ⅱ)设![]() ,
,![]()
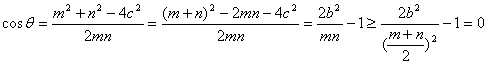
当且仅当![]() 时,
时,![]() . ∴
. ∴![]() ……………………… 8/
……………………… 8/
(Ⅲ)由(Ⅰ)得![]()
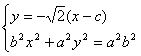
![]()

![]() ,
,
![]() ……………………… 11/
……………………… 11/
![]()
∴![]()
∴椭圆的方程为![]() ………………………………… 14/
………………………………… 14/