2006届高三数学高考模拟考试卷二
第Ⅰ卷 （选择题）
一、选择题：（本大题共12小题，每小题5分，共计60分）
1、若
的展开式中含有常数项（非零），则正整数n的可能值是
A．3 B．4 C．5 D．6
2、
的值是
A．
B．－
C．
D．－
3、函数
的反函数是
A．
B．
C．
D．
4、从1,2，3,…，9中任取两个数，其和为偶数的概率是
A．
B．
C．
D．
5、已知O为ΔABC所在平面内一点，满足
,则点O是ΔABC的
A. 外心 B. 内心 C. 垂心 D. 重心
6、已知m、l是直线，
、
、
是平面，下列命题中正确的有
①若m∥l，m⊥，则l⊥ ； ②若m∥l，m∥，则l∥；
③若
＝l ，l∥，m
，m⊥，则l⊥m，m∥ ；
④若＝m，＝l，∥，则m∥l.
A．4个 B．3个 C．2个 D．1个
7、若
，则下列四个数中，最大的是
A．
B．
C．
D．－1
8、直线
经过点P(2,1)，且与两坐标轴围成的三角形的面积为S，如果符合条件的直线能作且只能作三条，则S=
A．3 B．4 C．5 D．8
9、甲、乙两公交车往返于相距24公里的A、B两地之间, 现两车分别从两地同时驶出, 甲每小时行驶36公里, 乙每小时行驶24公里, 到达异地后立即返回, 若不计转向时间, 则从开始到4小时止, 他们相遇次数为
A. 4次 B. 5次 C. 6次 D. 7次
10、正方体ABCD—A1B1C1D1的棱长为1，在正方体表面上与点A距离是
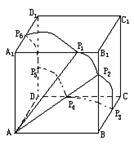
的点形成一条曲线，这条曲线的长度是
A. 
B.
C. 
D.
11、有5个座位连成一排，现安排3个人就座，则有两个空位不相连的不同坐法共
A.28种 B.36种 C.60种 D.72种
12、双曲线＝1的左焦点为F1，顶点为A1，A2，P是双曲线上任意一点，则分别以线段PF1、A1A2为直径的两圆位置关系为
A.相交 B.相切 C.相离 D.以上情况都有可能.
第Ⅱ卷（非选择题）
二、填空题（t本大题共4小题，每小题4分，共计16分）
13、不等式
的解集为 .
14、函数
在区间
上是单调函数，且最大值为
，则实数
________________.
15、在平面几何中,
的
内角平分线
分
所成线段的比
。把这个结论类比到空间：在三棱锥A—BCD中（如图）平面
平
分二面角
且与相交于
，则得到类比的结论是 .
 |
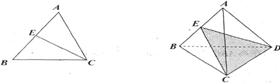16、对于任意
成立，则称函数
具有性质M.给出下列四个函数：①
，②
③
，④
.其中具有性质M的函数是 .（注：把满足题意的所有函数的序号都填上）
三、解答题：（本大题共6小题，共计74分x）
17、（本小题满分12分）
已知向量
.
（1）求函数的最小正周期及单调减区间；
（2）画出函数在区间
的图象，及在此区间上函数的对称轴和对称中心.
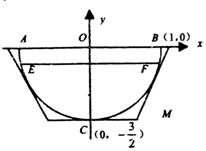
18、（本小题满分12分）
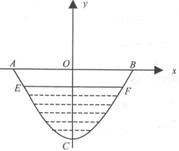设计如图所示一水渠，它的横截面曲线是抛物线形，AB宽2m，渠OC深为1.5m，水面EF距AB为0.5m.
（1）求截面图中水面宽度；
（2）由于情况有变，现要将此水渠改造为横截面是等腰梯形，要求渠深不变，不准往回填土，只准挖土，试求截面梯形的下边长为多大时，才能使所挖的土最少？
19、（本小题满分12分）
已知实数集R上的函数
其中a、b、c、d是实数.
（1）若函数在区间
上都是增函数，在区间（－1，3）上是减函数，并且
，求函数的表达式；
（2）若a、b、c满足
求证：函数是单调函数.
20、（本小题满分12分）
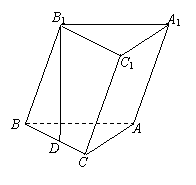已知斜三棱柱ABC—A1B1C1的底面是直角三角形，∠C=90°，侧棱与底面所成的角为α（0°＜α＜90°），点
在底面上的射影
落在
上．
（1）求证：AC⊥平面BB1C1C；
（2）当α为何值时，AB1⊥BC1，且使D恰为BC中点？
（3）若α = arccos ，且AC=BC=AA1时,求二面角C1—AB—C的大小.
21、（本小题满分12分）
已知正项数列
满足
，且
．
（1）求证：
；
（2）求证：
． 22、（本小题满分14分）
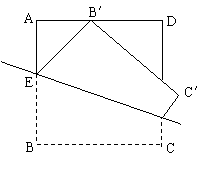如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B′；折痕l与AB交于点E，点M满足关系式
.
(1)建立适当的直角坐标系，求点M的轨迹方程；
(2)若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的，F是AB边上的一点， = 4，过点F的直线交曲线C于P、Q两点，且→PF=λ→FQ，求实数λ的取值范围.
2006届高三数学
高考模拟考试参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | C | C | C | A | B | B | D | B | B |
二、填空题：
13、
14、
15、
16、①③
三、解答题：
17、解：（1）
＝
故：
，令：
，则：
即为单调减区间。
（2）图象略，函数在上对称中心为
，对称轴不存在。
18、解：（1）建立如图所示坐标系
则抛物线方程为
当y=0.5时，
∴水面宽
（2）如图，设抛物线一点
（t>0）
因改造水渠中准挖土，而且要求挖出的土最少，所以只能沿过点M与抛物线相切的切线挖土。
由
,求导得y’=3x ∴过点M的切线斜率为3t
切线方程为：
令y=0，则
故截面梯形面积为：
当且仅当
时所挖土最少，此时下底宽
m。
答：故截面梯形的下底边长为0.707米宽时，才能使所挖的土最少。
19、解：（1）∵
∴d=－7
∴c=－18，
∴
∵函数
在区间
上都是增函数，
在区间（－1，3）上是减函数， ∴－1和3必是
的两个根，
∴
∴
.
（2）
由条件
为二次三项式，并且
∴当a>0时，
>0恒成立，此时函数
是单调增函数，
当a<0时，<0恒成立，此时函数是单调减函数，
∴对任意给定的非零实数a，函数
总是单调函数.
20、（1）∵ B1D⊥平面ABC， AC平面ABC，
B1D⊥AC,
又AC⊥BC, 
BC∩B1D=D． ∴ AC⊥平面BB1C1C．
(2) ∵ AC⊥平面BB1C1C ，要使AB1⊥BC1 ，由三垂线定理可知，只须B1C⊥BC1，
∴ 平行四边形BB1C1C为菱形， 此时，BC=BB1．
又∵ B1D⊥BC, 要使D为BC中点，只须B1C= B1B，即△BB1C为正三角形，
∴ ∠B1BC= 60°． ∵ B1D⊥平面ABC，且D落在BC上，
∴ ∠B1BC即为侧棱与底面所成的角．
故当α=60°时，AB1⊥BC1，且使D为BC中点．
（3）过C1作C1E⊥BC于E，则C1E⊥平面ABC．
过E作EF⊥AB于F，C1F，由三垂线定理，得C1F⊥AB．
∴∠C1FE是所求二面角C1—AB—C的平面角． 设AC=BC=AA1=a，
在Rt△CC1E中，由∠C1BE=α=
，C1E=
a．
在Rt△BEF中，∠EBF=45°，EF=
BE=a．
∴∠C1FE=45°，故所求的二面角C1—AB—C为45°．
解法二：（1）同解法一
（2）要使AB1⊥BC1，D是BC的中点，即
=0，=，
∴
， 
=0，∴
．
∴
，故△BB1C为正三角形，∠B1BC=60°；
∵ B1D⊥平面ABC，且D落在BC上， ∴ ∠B1BC即为侧棱与底面所成的角．
故当α=60°时，AB1⊥BC1，且D为BC中点．
（3）以C为原点，CA为x轴，CB为y轴，经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系，则A（a，0，0），B（0，a，0），C（0，－
，a），
平面ABC的法向量n1=（0，0，1），设平面ABC1的法向量n2=（x，y，z）．
由
n2=0，及
n2=0，得
∴n2=（
，，1）． cos<n1,
n2>＝= ，
故n1 , n2所成的角为45°，即所求的二面角为45°．
21、解：（1）因为an + 1
(n∈N*)且为正数，所以
，
所以
(n∈N*) （＊），
在（＊）中分别令n取n-1,n-2,…,3,2,1，将得到的n-1个代数式相加得：
+（n – 1），an 
(n∈N*)．
（2）由已知an 
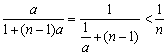（∵0 < a < 1），
所以
=
．
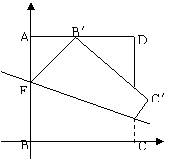22、（1）在BC所在的直线为x轴，以BA所在的直线为y轴，建立如图所示的直角坐标系。
设
，则
，从而直线的斜率为
。 设
的中点为G，则
。
故直线的方程为：
，从而得点
，由得：
，所以：
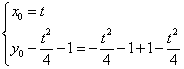，即：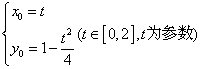
，消去t得：
即为点M的轨迹方程。
（2）由题意知：曲线C的方程为
，
。
设
与联立，得：
。
设
，则
① 
②
③
由①②③得：
，而
，所以
，故：
。