2000-2005全国高中数学竞赛不等式试题
2004年全国高中数学联赛试卷(第一试)
3、不等式
>0的解集是 ( )
A．[2，3] B。（2，3） C。[2，4] D。（2，4）
[答案]3、解：原不等式等价于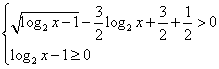
设
解得
。
即
。 故选C。
2003年全国高中数学联赛(第一试)
7．不等式
的解集是______________
9. 已知 
若
，则实数
的取值范围是_____________.
13．
设
证明不等式 
[答案]7.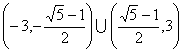 
. 提示： 原不等式可以化为:
9. 
提示：
,令
,
,则只需
在（1，3）上的图象均在x轴的下方，其充要条件是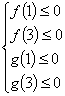
,由此推出;
13．
证明：由
可得
当且仅当a=b=c=d时取等号 ……5分
则
……………………………………………………15分
因为
不能同时相等，所以
……………………………………20分
2001年全国高中数学联赛试卷
4．如果满足∠ABC=60°，AC=12，BC=k的△ABC恰有一个，那么k的取值范围是（ ）
（A）k=
（B）0<k≤12 （C） k≥12（D） 0<k≤12或k=
6．已知6枝玫瑰与3枝康乃馨的价格之和大于24元，而4枝玫瑰与5枝康乃馨的价格之和小于22元，则2枝玫瑰的价格和3枝康乃馨的价格比较结果是（ ）
（A） 2枝玫瑰价格高 （B） 3枝康乃馨价格高
（C） 价格相同 （D） 不确定．
10. 不等式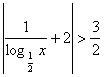
的解集为 ．
11．函数
的值域为
[答案]．4．D 6．A
10． 
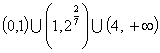11．
2000年全国高中数学联赛 (第一试)
10．已知
是定义在
上的函数，
且对任意
都有
若
，则
．
11．若
，则
的最小值是 ．
12．使不等式
对一切恒成立的负数的取值范围是 ．
[答案]10. 解：由，得
，所以
即
，
∴
∴
即
是周期为1的周期函数，又
，故
11. 解：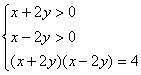
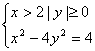
由对称性只考虑
，因为
，所以只须求
的最小值．
令
公代入
，有
．
这是一个关于
的二次方程显然有实根，故
，∴
当
，
时，
．故的最小值为
12. 解：原不等式可化为
∵
，
，
∴当
时，函数
有最大值
，
从而有
，整理得
∴
或
，又，∴
1999年全国高中数学联合竞赛三、(满分20分)已知当xÎ[0,1]时，不等式
恒成立，试求的取值范围．
[答案]13. 若对一切xÎ［0，1］，恒有f(x)= ，
则 cosθ=f(1)>0, sinθ=f(0)>0. (1)
取xÎ (0，1)，由于 
，
所以，
恒成立，当且仅当 
(2 )
先在［0,2π］中解(1)与(2)：由cosθ>0,sinθ>0，可得0<θ<
.
又由（2）得 sin2θ>
注意到0<2θ<π，故有
<2θ< 
,
所以，
<θ<
.
因此，原题中θ的取值范围是2kπ+<θ<2kπ+ ,kÎZ.
或解：若对一切x∈［0，1］，恒有
f(x)=x2cosθ-x(1-x)+(1-x)2sinθ>0，
则cosθ=f(1)>0,sinθ=f(0)>0. (1)
取 x0= 
∈(0，1)，则 
．
由于 
+2
x(1-x)，
所以，0<f(x0)=2x0(1-x0)
．
故 -
+
>0
(2)
反之，当(1)，(2)成立时，f(0)=sinθ>0，f(1)=cosθ>0，且x∈(0，1)时，f(x)≥2x(1-x)>0．
先在［0,2π］中解(1)与(2)：
由cosθ>0,sinθ>0，可得0<θ<
.
又-+>0,
> ,
sin2θ>
,
sin2θ>,
注意到 0<2θ<π，故有 
<2θ<
,
所以，
<θ<
.
因此，原题中θ的取值范围是 2kπ+<θ<2kπ+
,k∈Z
首届中国东南地区数学奥林匹克
（2004年7月11日 8：00 — 12：00 温州）
五、已知不等式
对于
恒成立，求a的取值范围。
[答案]五、解：设
，则
从而原不等式可化为：
即
，
原不等式等价于不等式（1）
（1）不等式恒成立等价于
恒成立。
从而只要
。
又容易知道
在
上递减，
。
所以
。
2004四年全国高中数学联合竞赛（天津初赛）
2．若
，且
，则下列各式中最大的是（ C ）
（A）
（B）
（C）
（D）
2004年全国高中数学联赛四川省初赛
1． 已知不等式m2＋(cos2θ－5)m＋4sin2θ≥0恒成立，则实数m的取值范围是A
A.0≤m≤4 B.1≤m≤4 C.m≥4或x≤0 D.m≥1或m≤0
8．不等式x2－2≤2x＋1的解集为__________________.8、{x－1≤x≤3}
10．若0＜a、b、c＜1满足条件ab＋bc＋ca＝1，则的最小值是____.
2005年全国高中数学联合竞赛浙江省预赛
10．设命题 P: 
和命题Q: 对任何，
有且仅有一个成立，则实数
的取值范围是
。
【解】： 命题 P成立 可得 
；
命题Q成立 可得 
。
因此，要使命题P和命题Q有且仅有一个成立，实数c的取值范围是 
2005年全国高中数学联赛江苏赛区初赛
3.设 
, 那么 
的最小值是
A. 2 B. 3 C. 4 D. 5
3,C
由 , 可知
所以， 
. 故选 C．