2006年上海市十校(高三)数学测试
| 总分 | 一 | 二 | 三 | |||||
| 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | |
一、填空题:(本大题满分48分)
1.若集合![]() ,则
,则![]() =
。
=
。
2.已知![]() 是偶函数,定义域为
是偶函数,定义域为![]() ,则
,则![]() =
。
=
。
3.函数![]() 的反函数是
。
的反函数是
。
4.函数![]() 的最小正周期是
。
的最小正周期是
。
5.函数![]() 的对称中心是
。
的对称中心是
。
6.已知等差数列![]() 的公差
的公差![]() ,且a1,a3,a9成等比数列,则
,且a1,a3,a9成等比数列,则![]() = 。
= 。
7. 在实数集R上定义运算∽:x∽y=x(1-y.),若(x-a)∽(x+a)<1对任意实数x都成立,则实数a的取值范围是 。
8.已知直线![]() ,为使这条直线不经过第二象限,则实数
,为使这条直线不经过第二象限,则实数![]() 的范围是
。
的范围是
。
9.在000,001,…,999,这1000个连号的自然数中抽奖,若抽到一个号码中,出现仅出现两个相同偶数则中奖,则一个号码能中奖的概率是 。
10.ΔABC的两条边上的高的交点为H,外接圆的圆心为O,![]() ,则实数m=
。
,则实数m=
。
11.如图,在ΔABC中BC=2,AB+AC=3,中线AD的长为y,若AB的长为x,则y与x函数关系式为
。
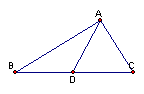
第11题图
12.若![]() ,则
,则![]() 。
。
二、选择题:(本大题满分16分)
13.设A、B是锐角三角形的两个内角,则复数![]() 对应点位于复平面的(
)。
对应点位于复平面的(
)。
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
14.直线![]() 绕原点逆时针方向旋转300后,所得直线与圆
绕原点逆时针方向旋转300后,所得直线与圆![]() 的位置关系是(
)。
的位置关系是(
)。
A.直线过圆心 B.直线与圆相交,但不过圆心
C.直线与圆相切 D.直线与圆没有公共点
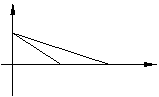
15.如图,OA是双曲线实半轴,OB是虚半轴,F是焦点,且![]() ,则双曲线的方程是(
)
,则双曲线的方程是(
)
 y
y
B
O A F x
第15题图
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.在ΔABC中,![]() ,则C等于( )
,则C等于( )
A.300 B.1500 C.300或1500 D.600或1200
二、解答题:(本大题满分86分)本大题共6题,解答各题必须写出必要的步骤。
17.(本题满分12分)已知x∈R,z∈C,x、z满足![]() 。
。
(1) 若z在复平面内对应的点Z在第一象限,求x的范围;
(2)
是否存在这样x,使![]() 成立。
成立。
18.(本题满分12分,第(1)6分,第(2)6分)
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如ΔDQH等)上铺草坪,造价为80元/m2。
(1) 设总造价为S元,AD长为xm,试建立S与x的函数关系;
(2) 当x为何值时,S最小?并求这个最小值。
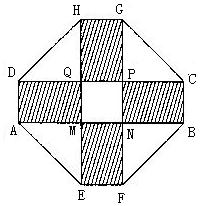
第18题图
19.(本题满分14分,第(1)小题6分,(2)小题8分)
设![]() 是
是![]() 上的奇函数,对任意实数x,都有
上的奇函数,对任意实数x,都有![]() ,当
,当![]() 时,
时,![]() 。
。
(1) 试证:![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
(2) 证明函数![]() 是以4为周期的函数,并求
是以4为周期的函数,并求![]() 时,
时,![]() 的解析式。
的解析式。
20.(本题满分14分,第(1)小题6分,(2)小题8分)
在平面直角坐标系中,若![]() ,且
,且![]() 。
。
(1)求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(2)过点(0,3)作直线![]() 与曲线C交于A、B两点,设
与曲线C交于A、B两点,设![]() ,是否存在这样的直线
,是否存在这样的直线![]() ,使得四边形OAPB为矩形?若存在,求出直线
,使得四边形OAPB为矩形?若存在,求出直线![]() 的方程,不存在,说明理由。
的方程,不存在,说明理由。
21.(本题满分16分,其中第(1)小题8分,第(2)小题8分)
已知存在实数![]() (其中
(其中![]() )使得函数
)使得函数![]() 是奇函数,且在
是奇函数,且在![]() 上是增函数。
上是增函数。
(1)试用观察法猜出两组![]() 与
与![]() 的值,并验证其符合题意;
的值,并验证其符合题意;
(2)求出所有符合题意的![]() 与
与![]() 的值。
的值。
22.(本题满分18分,其中第(1)小题6分,第(2)小题6分,第(3)小题6分)
如图所示,是树形图形.第一层是一条与水平线垂直的线段,长度为1;第二层在第一层线段的前端作两条与该段均成1350的线段,长度为其一半;第三层按第二层的方法在每一线段的前端生成两条线段;重复前面的作法作图至第n层.设树形图的第n层的最高点到水平线的距离为第n层树形图的高度。
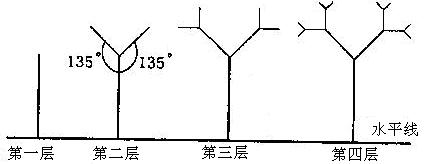
1)求第三层及第四层树形图的高度H3,H4;
2)求第n层树形图的高度Hn;
3)若树形图的高度大于2,则称树形图为“高大”,否则称为“矮小”。显然,当![]() 时是“矮小”的,是否存在
时是“矮小”的,是否存在![]() 。使得当
。使得当![]() 时,该树形图是“高大”的?
时,该树形图是“高大”的?
参考答案及评分标准
一、填空题
1.![]() 。
。
2.![]() 。提示:定义域关于原点对称
。提示:定义域关于原点对称![]() 。
。
3.![]() 。
。
4.л。提示:![]() ,知
,知![]() 。
。
5.![]() 。
。
6. ![]() 。提示:因为a1,a1+2d,a1+8d成等比数列,所以(a1+2d)2=a1(a9+9d),所以a1=d,所以
。提示:因为a1,a1+2d,a1+8d成等比数列,所以(a1+2d)2=a1(a9+9d),所以a1=d,所以![]() 。
。
7.![]() 。提示:由定义有
。提示:由定义有
(x-a)∽(x+a)<1![]() 对
对![]() 都成立,由
都成立,由![]() 即得
即得![]() 。
。
8.![]() 。提示:显然直线经过定点
。提示:显然直线经过定点![]() ,又当
,又当![]() 时,
时,![]() ,不经过第二象限,当
,不经过第二象限,当![]() 时,
时,![]() 要使直线不经过第二象限,只需
要使直线不经过第二象限,只需![]() ,综上
,综上![]() 。
。
9.![]() 。提示:总共有1000个号码,抽到有两个相同偶数的情况可以分两类:一类是3个偶数,其中两个相同,如422,242,224,共有
。提示:总共有1000个号码,抽到有两个相同偶数的情况可以分两类:一类是3个偶数,其中两个相同,如422,242,224,共有![]() ;另一类是两个相同偶数,另一个是奇数,如500,050,005等,共有
;另一类是两个相同偶数,另一个是奇数,如500,050,005等,共有![]() ,故
,故![]() 。(或
。(或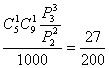 )
)
10.1.提示:令∠A=900,则O为BC的中点,H为A点,此时所给等式变为![]() 。
。
另解:取BC的中点D,则![]() ,且只有OD⊥BC,AH⊥BC,由
,且只有OD⊥BC,AH⊥BC,由![]() ,
,
![]() 。
。
11.![]() ;提示:
;提示:![]()
![]() ,两式相加整理得
,两式相加整理得![]() ,其中
,其中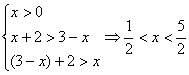 。
。
12.![]() 。提示:
。提示: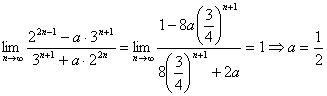 。
。
二、选择题
13.B.提示![]() ,
,![]()
同理![]()
另解:取A=B=C=600可得B。
14.C.提示:已知直线的倾斜角为300,旋转后的直线的倾斜角为600,其直线方程为![]() ,圆心到直线的距离为
,圆心到直线的距离为![]() 等于圆的半径。
等于圆的半径。
15.B.提示:由题意,![]() ,
,
于是![]() ,所以
,所以![]() 从而
从而![]() ,所以双曲线的方程为
,所以双曲线的方程为![]() 。
。
16.A.提示:两式平方相加得![]() ,所以A+B=300或1500,若A+B=300,则
,所以A+B=300或1500,若A+B=300,则![]() 与
与![]() 矛盾。所以C=300。
矛盾。所以C=300。
三、解答题
17.解:(1)![]()
当![]() ,即
,即![]() 时,
时,![]() 矛盾,所以
矛盾,所以![]() 。
。
所以![]() , ------------------3分
, ------------------3分
由题意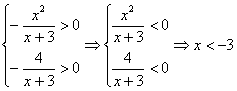 ------------------6分
------------------6分
(2)假设存在这样的x,使![]() 则
则
![]() ,------------------------9分
,------------------------9分
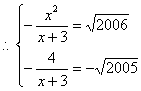 ,方程组无解,所以这样的x不存在。 ---------------12分
,方程组无解,所以这样的x不存在。 ---------------12分
18.解:(1)设DQ=y, 又AD=x,则![]() ,
,
![]() ,----------------------------------------------------------------------3分
,----------------------------------------------------------------------3分
![]()
![]() 。-----------------------------------------------------6分
。-----------------------------------------------------6分
(2)![]() ,--------------------------------------10分
,--------------------------------------10分
当且仅当![]() ,即
,即![]() 时,
时,![]() 元。----------12分
元。----------12分
19.(1)因为![]() 为奇函数,所以
为奇函数,所以![]() ,所以
,所以![]() ,--3分
,--3分
所以![]() ,
,
所以![]() 是函数
是函数![]() 的一条对称轴;-------------------------------------------------6分
的一条对称轴;-------------------------------------------------6分
(2)![]() ,
,
所以![]() 是以4为周期的函数。------------------------------------------------10分
是以4为周期的函数。------------------------------------------------10分
又![]() 时,
时,![]() 。
。
当![]() ,
,
当![]()
所以![]() 时,
时,![]() 的解析式为
的解析式为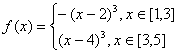 ----------14分
----------14分
另解:![]() 在
在![]() 上的图象如下:
上的图象如下:
![]() y
y
![]()
![]() - 1
- 1
![]()
![]()
![]()
![]()
![]() ∣ ∣ ∣
x
∣ ∣ ∣
x
- -1
所以![]() 时,
时,![]() 的解析式为
的解析式为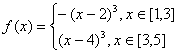
20.(1)因为![]() ,且
,且![]() 。
。
所以动点M到两个定点F1(0,-2),F2(0,2)的距离的和为8。
所以轨迹C以F1(0,-2),F2(0,2)为焦点的椭圆,方程为
![]() -------------------------------------------------------------------------------------6分
-------------------------------------------------------------------------------------6分
(2)为直线![]() 过点(0,3)。
过点(0,3)。
若直线![]() 是y轴,则A、B是椭圆的顶点。
是y轴,则A、B是椭圆的顶点。![]() ,所以O与P重合,与四边形OAPB是矩形矛盾。--------------------------------------------------------------------------9分
,所以O与P重合,与四边形OAPB是矩形矛盾。--------------------------------------------------------------------------9分
所以直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]()
由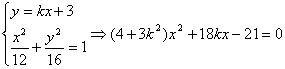 ,
,
由于![]() 恒成立。
恒成立。
由韦达定理![]() ---------------------------------11分
---------------------------------11分
因为![]() ,所以OAPB是平行四边形。
,所以OAPB是平行四边形。
若存在直线![]() ,使得四边形OAPB为矩形,则OA⊥OB,即
,使得四边形OAPB为矩形,则OA⊥OB,即![]() ,
,
因为![]()
所以![]() ,-----------------------------------------------12分
,-----------------------------------------------12分
所以![]() ,
,
所以![]()
机![]() ,
,
故存在直线![]() ,使得四边形OAPB为矩形。---------------14分
,使得四边形OAPB为矩形。---------------14分
21.解:(1)猜想: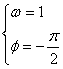 或
或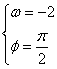 ;--------------------------------4分
;--------------------------------4分
由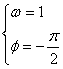 知
知![]() ,而
,而![]() 为奇函数且在
为奇函数且在![]() 上是增函数。-------------------------------------------------------------------------6分
上是增函数。-------------------------------------------------------------------------6分
由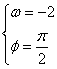 知
知![]() ,而
,而![]() 为奇函数且在
为奇函数且在![]() 上是增函数。-------------------------------------------------------------------------------------------8分
上是增函数。-------------------------------------------------------------------------------------------8分
(2)由![]() 为奇函数,有
为奇函数,有![]()
所以![]() ,又
,又![]() ,
,
解得![]() 。-----------------------------------------------------------------------------10分
。-----------------------------------------------------------------------------10分
当![]() 时,
时,![]() 为奇函数,由于
为奇函数,由于![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,由
,由![]() ,又
,又![]() 在
在![]() 上是增函数,故有
上是增函数,故有![]() ,且
,且![]() 或
或![]() ,故
,故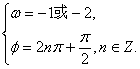 。----------------------------------------------------------------------------12分
。----------------------------------------------------------------------------12分
当![]() 时,
时,![]() 为奇函数,由于
为奇函数,由于![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,由
,由![]() ,又
,又![]() 在
在![]() 上是增函数,故有
上是增函数,故有![]() ,且
,且![]() 或2,故
或2,故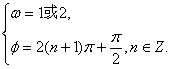 ------------------------------------------------------------14分
------------------------------------------------------------14分
所以所有符合题意的![]() 与
与![]() 的值为:
的值为:
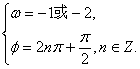 或
或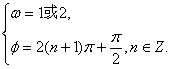 --------------------------------------16分
--------------------------------------16分
22.(1)设题中树(从下而上)新生的各层高度所构成的数列为![]() ,则
,则![]() ,-------------------------------------------4分
,-------------------------------------------4分
所以,第三层树形图的高度![]() 。---------------------------5分
。---------------------------5分
第三层树形图的高度![]() 。-------------------------6分
。-------------------------6分
(2)易知![]() ,所以第n层树形图的高度为
,所以第n层树形图的高度为
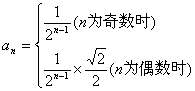 ,----------------------------------------------------------9分
,----------------------------------------------------------9分
所以,当为奇数时,第n层树形图的高度为
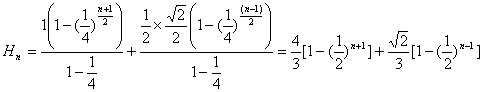 ;---10分
;---10分
当为偶数数时,第n层树形图的高度为
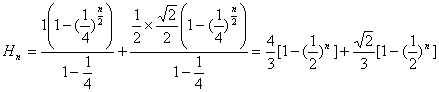 。------------12分
。------------12分
(1) 不存在。
由(2)知,当为奇数时,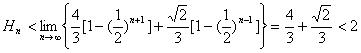 ;-----------------------------------------------------------------------------------------------------15分
;-----------------------------------------------------------------------------------------------------15分
当为偶数数时, ,--------------17分
,--------------17分
由定义,此树形图是永远是“矮小“的。所以不存在![]() 。使得当
。使得当![]() 时,该树形图是“高大”的。------------------------------------------------------------------18分
时,该树形图是“高大”的。------------------------------------------------------------------18分