2005-2006年第二学期扬州中学高三第一次月考数学试卷
2006.2
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
第Ⅰ卷 (选择题 共60分)
一、选择题:(本大题共计12小题,每小题5分,共60 分)
1.设![]() ,集合A={xf(x)=x,x∈R},B={xf[f(x)]=x,x∈R},则A与B的关系是
( )
,集合A={xf(x)=x,x∈R},B={xf[f(x)]=x,x∈R},则A与B的关系是
( )
A.A∩B=A B.A∩B=φ C.A∪B=R D.A∪B={-1,0,1}
2.抛物线![]() 的焦点坐标是
( )
的焦点坐标是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于 ( )
等于 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.4男5女排成一排,4男顺序一定,5女顺序也一定的排法种数为 ( )
A. 15120 B. 126 C. 3024 D. 以上答案都不对
5. 若![]() ,则“
,则“![]() ”是“方程
”是“方程![]() 表示双曲线”的 ( )
表示双曲线”的 ( )
(A)充分不必要条件. (B)必要不充分条件.
(C)充要条件. (D)既不充分也不必要条件.
6. 若![]() ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
7.若向量![]() =(-2,1),
=(-2,1),![]() =(3,-x),且
=(3,-x),且![]() 与
与![]() 的夹角为钝角,则x的取值范围为 ( )
的夹角为钝角,则x的取值范围为 ( )
A.{xx>-6} B.{xx<-6} C.{xx≥-6}
D.{xx>-6且x≠![]() }
}
8. 设直线![]() 的倾斜角为
的倾斜角为![]() ,则该直线关于直线
,则该直线关于直线![]() (
(![]() )对称的直线的倾斜角为 ( )
)对称的直线的倾斜角为 ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
9. 过点(1,2)总可以作两条直线与圆x2+y2+kx+2y+k2-15=0相切,则实数k的取值范围( )
(A)k>2 (B)-3<k<2 (C)k<-3或k>2 (D)都不对
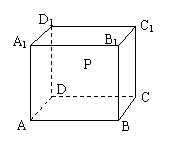 10.如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1的距离是点P到直线BC的距离的2倍,则动点P的轨迹为
( )
10.如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1的距离是点P到直线BC的距离的2倍,则动点P的轨迹为
( )
A. 圆弧
B. 椭圆的一部分
C. 双曲线的一部分
D. 抛物线的一部分
11.在△ABC中,有下列命题:
①A>B的充要条件为sinA>sinB; ②A<B的充要条件为cosA>cosB;
③若A,B为锐角,则sinA+sinB>cosA+cosB; ④tan![]() tan
tan![]() 为常数
为常数
其中正确的命题的个数为 ( )
A. 1个 B. 2个 C. 3个 D. 4个
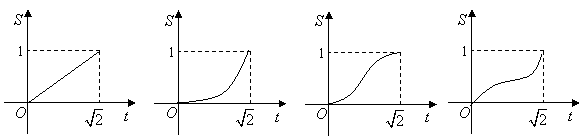
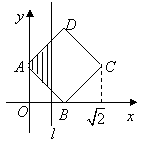 12.如图,正方形
12.如图,正方形![]() 的顶点
的顶点![]() ,
,![]() ,顶点
,顶点![]() 位于第一象限,直线
位于第一象限,直线![]() 将正方形
将正方形![]() 分成两部分,记位于直线
分成两部分,记位于直线![]() 左侧阴影部分的面积为
左侧阴影部分的面积为![]() ,则函数
,则函数![]() 的图象大致是
的图象大致是
 |
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
第二卷(非选择题共90分)
二. 填空题:(本大题共6小题,每小题4分,共24分,请把答案直接填在题中横线上)
13.把函数y=2x2-4x+5的图象按向量a平移,得到y=2x2的图象,且a⊥b,c=(1,-1),
b•c=4,则b= 。
14.直角坐标系![]() 中,若定点
中,若定点![]() 与动点
与动点![]() 满足
满足 ![]() ,则点
,则点![]() 的轨迹方程是
。
的轨迹方程是
。
15.将一张坐标纸折叠一次,使得点(0, 2)与(-2, 0)重合,且直线l1与直线l2重合,若l1的方程为2x+3y-1=0,则l2的方程为 。
16.设![]() ,
,![]() 是两个不共线的向量,若
是两个不共线的向量,若![]() ,
,![]() ,
,![]() ,且
,且![]() 三点共线,则
三点共线,则![]() _______ 。
_______ 。
17.曲线![]() 与直线
与直线![]() 的交点个数是
。
的交点个数是
。
18.若函数![]() 的图象与直线
的图象与直线![]() 有且仅有四个不同的交点,则
有且仅有四个不同的交点,则![]() 的取值范围是__________。
的取值范围是__________。
三. 解答题:(本大题共5小题,共66分,解答应写出文字说明,证明过程或演算步骤)
19. (本小题满分12分) 已知△ABC的面积S满足 ![]() , 且
, 且 ![]() ,
, ![]() 与
与![]() 的夹角为
的夹角为![]() .
.
(I) 求![]() 的取值范围;
的取值范围;
(II)求函数![]() 的最小值.
的最小值.
20.(本小题满分12分) 如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 折到点
折到点![]() 的位置,且二面角
的位置,且二面角![]() 的大小为
的大小为![]() 。
。
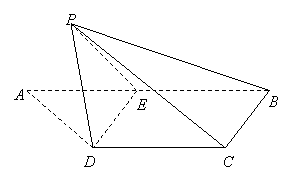 (1)求证:
(1)求证:![]()
(2)求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小
(3)求点![]() 到平面
到平面![]() 的距离
的距离
21.(本题满分14分)
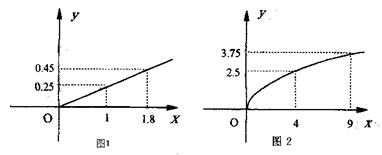
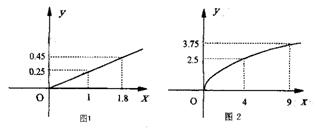
某民营企业生产A、B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位:万元)
(1)分别将A、B两种产品的利润表示为投资的函数关系式写出。
(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润约为多少万元?(精确到1万元)
|
22.(本题满分14分)
已知二次函![]()
![]() 。
。
(1)求a,b,c的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)令![]()
23.(本题满分14分) 对于函数 ![]() ,若存在
,若存在![]() ,使
,使 ![]() 成立,
成立,
则称![]() 为
为![]() 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = ![]() .
.
(I)试问![]() 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列![]() 的各项均为负数,且满足
的各项均为负数,且满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(III)已知![]() ,求
,求![]() 的前项和
的前项和![]() .
.
参考答案及评分标准:
一.选择题:(每小题5分,共60 分)
1.A 2.D 3.B 4.B 5.A 6.C 7.D 8.D 9.D 10.B 11.C 12.C
二.填空题:(每小题4分,共24分)
13. (3 , -1) 14. x+2y=4 15. 3x+2y+1=0 16. -8
17. 3 18. [1 , ![]() ]
]
三.解答题:
19.(12分) 解:(1)由题意知,![]()
![]()
![]() , ………………①
, ………………①
![]()
![]()
![]()
![]()
![]()
![]() ,…………②………(2分)
,…………②………(2分)
由②÷①, 得![]() , 即
, 即![]()
由![]() 得
得![]() , 即
, 即![]() .……………(4分)
.……………(4分)
又![]() 为
为![]() 与
与![]() 的夹角, ∴
的夹角, ∴![]() , ∴
, ∴![]() .……………(6分)
.……………(6分)
(2)![]()
![]() ……………(9分)
……………(9分)
∵![]() , ∴
, ∴![]() .……………(10分)
.……………(10分)
∴![]() , 即
, 即![]() 时,
时, ![]() 的最小值为3. ……………(12分)
的最小值为3. ……………(12分)
20.(12分)(1)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,即
,即![]() 平分
平分![]() ,
,![]() 是正三角形,
是正三角形,
![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]()
(2)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角。
所成的角。
![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,在
,在![]() 中,
中,
![]() ,
,![]() 直线
直线![]() 与平面
与平面![]() 所成角是
所成角是![]()
(3)![]() ,
,![]() 在平面
在平面![]() 外,
外,![]() ,
,![]() 点到面
点到面![]() 的距离即为点
的距离即为点![]() 到面
到面![]() 的距离,过点
的距离,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 的长即为点
的长即为点![]() 到面
到面![]() 的距离,菱形
的距离,菱形![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
|
解:(1)设投资为x万元,A产品的利润为 f (x) 万元,B产品的利润为 g (x) 万元
由题设![]()
由图知![]()

(2)设A产品投入x万元,则B产品投入10-x万元;设企业利润为y万元。
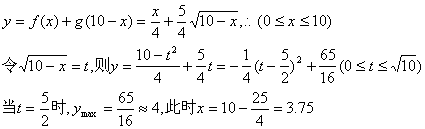
答:当A产品投入3.75万元,B产品投入6.25万元时,企业获得大利润约4万元。
22.(本题满分14分)
解:(1)![]()
![]()
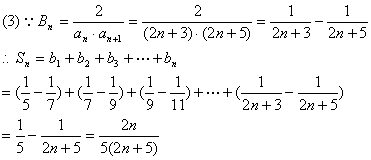
23.(14分)
解:(I)由![]() 令
令![]()
![]()
![]() 解得
解得![]()
即f(x)存在两个滞点0和2
![]()
(II)由题得![]() ,
,![]() ①
①![]()
故![]() ②
②
由②-①得![]() ,
,![]()
![]()
![]() ,即
,即![]() 是等差数列,且
是等差数列,且![]()
![]()
当n=1时,由![]()
![]()
![]()
(III)![]() ③
③
![]() ④
④
由④-③得![]()
![]()
![]()