高三文科练习
1、已知集合![]() ( )
( )
A.{(-1,2)} B.![]() C.P D.Q
C.P D.Q
2、若不等式![]() 成立的充分非必要条件是
成立的充分非必要条件是![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、已知命题p:若a、b∈R,则a+b>1是a+b>1的必要条件. 命题q:函数![]() 的值域是
的值域是![]() ,则 ( )
,则 ( )
A.p或q为假 B.p且q为假
C.p且q为真 D.非p或非q为真
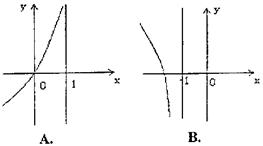
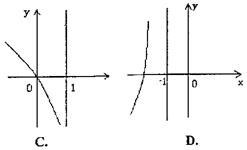
4、已知函数f(x)=2x+1, 则f-1(-x)的图象只可能是 ( )
5、对于函数![]() ,有下列四个命题:①
,有下列四个命题:①![]() 是奇函数;②
是奇函数;②![]()
③![]() 在R上是增函数;④
在R上是增函数;④![]() 有最小值0,其中正确命题的序号是 ( )
有最小值0,其中正确命题的序号是 ( )
A.①③④ B.①②③ C.②③④ D.①②④
6、已知![]() 且
且![]() 与
与![]() 共线,
共线,![]() 与
与![]() 不共线若
不共线若![]() ,则
,则![]() =
( )
=
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、已知向量![]() 则
则![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.
B.![]() C.-1 D.-3
C.-1 D.-3
8、给出下列三个命题:(1)函数![]() 的最小正周期为
的最小正周期为![]() ;(2)函数
;(2)函数
![]() 上单调递增; (3)
上单调递增; (3)![]() 是函数
是函数![]() 的图象 的一条对称轴.其中正确命题的个数是 ( )
的图象 的一条对称轴.其中正确命题的个数是 ( )
A.0 B.1 C.2 D.3
9、数列![]() 的值为 ( )
的值为 ( )
A.-a B.a C.a-b D.b
10、等差数列![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、数列![]() 的前n项和为 ( )
的前n项和为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12、已知每生产100克饼干的原材料加工费为1.8元.某食品加工厂对饼干采用两种包装,其包装费用、销售价格如下表所示:
| 型号 | 小包装 | 大包装 |
| 重量 | 100克 | 300克 |
| 包装费 | 0.5元 | 0.7元 |
| 销售价格 | 3.00元 | 8.4元 |
则下列说法正确的是 ( )
①买小包装实惠;②买大包装实惠;③卖3小包比卖1大包盈利多;④卖1大包比卖3小包盈利多.
A.①③ B.①④ C.②③ D.②④
13、已知平面,α,β,γ及直线l,m满足:l⊥m,α⊥γ,γ∩α=m,γ∩β=l,则由此可推出:①β⊥γ,②l⊥α,③m⊥β ( )
A.①和② B.② C.①和③ D.②和③
14、设![]() ,
,![]() ,
,![]() 是空间三条直线,
是空间三条直线,![]() ,
,![]() 是空间两个平面,则下列命题中,逆命题不成立的是 ( )
是空间两个平面,则下列命题中,逆命题不成立的是 ( )
A.当![]() 时,若
时,若![]() ,则
,则![]() ∥
∥![]() B.当
B.当![]() 时,若
时,若![]() ,则
,则![]()
C.当![]() ,且
,且![]() 是
是![]() 在
在![]() 内的射影时,若
内的射影时,若![]() ,则
,则![]()
D.当![]() ,且
,且![]() 时,若
时,若![]() ,则
,则![]()
15、在半径为1cm的球面上有A、B、C三点,如果AB=8![]() ,∠ACB=60°,则球心O到
,∠ACB=60°,则球心O到
平面ABC的距离为 ( )
A.2cm B.4cm C.6cm D.8cm
16、椭圆![]() 的两个焦点是F1、F2,以F1F2为边作正三角形,若椭圆恰
的两个焦点是F1、F2,以F1F2为边作正三角形,若椭圆恰
平分三角形的另两边,则椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17、集合![]() ,其中
,其中![]() .且
.且![]() 把满足上述条件的一对有序整数对(
把满足上述条件的一对有序整数对(![]() )作为一个点的坐标,则这样的点的个数是
( )
)作为一个点的坐标,则这样的点的个数是
( )
A.9个 B.14个 C.15个 D.21个
18、已知![]() ( )
( )
A.0 B.1 C.512 D.1024
19、二项式![]() 展开式中系数最小的项是 ( )
展开式中系数最小的项是 ( )
A.第42项 B.第21项 C.第22项 D.第41项
20、一射手射击时其命中率为0.4,则该射手命中的平均次数为2次时他需射击 ( )次。
A.2 B.3 C.4 D.5
21、已知函数![]() 的导函数
的导函数![]() 的图象如右图则关于函数
的图象如右图则关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
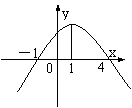 A.在
A.在![]() 处取极大值
处取极大值
B.在![]() 处取极小值
处取极小值
C.在区间![]() 上是减函数
上是减函数
D.在区间![]() 上是增函数
上是增函数
22、已知实数x, y满足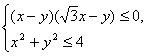 ,则不等式组表示的平面区域的面积为
.
,则不等式组表示的平面区域的面积为
.
23、已知向量![]() 分别是与x轴,y轴方向相同的单位向量),且
分别是与x轴,y轴方向相同的单位向量),且![]() ,则动点M(x, y)的轨迹方程为
.
,则动点M(x, y)的轨迹方程为
.
24、正四棱锥P—ABCD的底面ABCD在球O的大圆面上,顶点P在球面上,已知球的体积为![]() ,则正四棱锥P—ABCD体积的最大值为
,则正四棱锥P—ABCD体积的最大值为
25、直线l经过点![]() ,并与抛物线
,并与抛物线![]() 只一个公共点,则直线l的方程是 .
只一个公共点,则直线l的方程是 .
26、已知平面内有一条线段AB,其长度为![]() ,一动点P满足
,一动点P满足![]() ,M为AB的中点,则
,M为AB的中点,则![]() 的最小值为 .
的最小值为 .
27、在(1+x)n的展开式中,奇数项之和为p,偶数项之和为q,则(1-x2)n等于
28、样本13、12、19、17、14的方差![]() =
.
=
.
29、已知某射手的射击水平为:击中10环的概率为![]() ,击中9环的概率为
,击中9环的概率为![]() ,击中8环的概率为
,击中8环的概率为![]() ,该射手共射三枪.
,该射手共射三枪.
(1)求第一枪中10环,第二枪中9环,第三枪中8环的概率;
(2)求三枪分别为10环,9环,8环的概率;
(3)求三枪总环数为27环的概率.
30、某人参加射击测试,射击一次击中的概率为![]() ,现有两个测试方案.
,现有两个测试方案.
方案一:要求射击四次,至少击中两次为合格,求此人合格的概率.
方案二:如果击中目标测试就结束,否则将继续进行,直到击中为止,但射击的次数最多不超过四次,求此人三次内结束射击的概率.(结果用最简分数表示)
31、已知方程x2+2mx+m+1=0( m∈R且m≠0)的两根是tanα、tanβ.
(1)求sin2(α+β)+2cos(α+β)sin(α+β)的值;
(2)若α、β为某三角形的两个内角,试求m的取值范围.
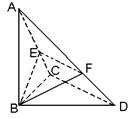
32、已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
|
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
33、函数![]()
(I)若![]()
(Ⅱ)若![]()
34、已知函数![]() 在区间[0,1]上单调递增,在区间[1,2]上单调递减.
在区间[0,1]上单调递增,在区间[1,2]上单调递减.
(1)求![]() 的表达式;
的表达式;
(2)设![]() 的解集恰好有3个元素,求b的取值范围;
的解集恰好有3个元素,求b的取值范围;
(3)设![]() 上恒成立,求c的取值范围.
上恒成立,求c的取值范围.
解答题答案:1、设射手射中10环、9环、8环的事件分别为A,B,C.
(1)因为A,B,C为相互独立事件,其同时发生的概率为
P(ABC)=P(A)·P(B)·P(C)=![]()
(2)因为8,9,10的排列有6种,即6种不同的排列为6种互斥事件,因此
![]()
(3)由于![]() 故三枪的环数只能是9,9,9或10,9,8,这是两种互斥事件,
故三枪的环数只能是9,9,9或10,9,8,这是两种互斥事件,
因此![]()
2、解(1)击中两次的概率为![]()
击中三次的概率为![]()
击中四次的概率为![]() ∴合格的概率P=P1+P2+P3=
∴合格的概率P=P1+P2+P3=![]() ……6分
……6分
(2)记第n次击中为事件Ai(i =1,2,3), 则A1,A2,A3,彼此互斥.
![]()
∴三次内击中的概率为:![]() …………………………12分
…………………………12分
3、解:由韦达定理得:![]()
又由于![]() ………………2分
………………2分
(1)而![]()
=![]()
=![]() …………………………………………6分
…………………………………………6分
=![]()
注:还可用倍角和万能公式求解
(2)α、β是三角形的内角,又tan(α+β)=2,所以α、β都是锐角,
即0<tanα<2、0<tanβ<2,令f(x)=x2+2mx+m+1
即m满足: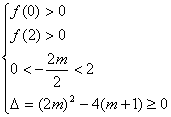 ………………………………(10分)
………………………………(10分)
解得:![]() ……………………………………………………(12分)
……………………………………………………(12分)
4、(1)∵AB⊥平面BCD, ∴AB⊥CD,∵CD⊥BC且AB∩BC=B, ∴CD⊥平面ABC. 3分
又![]() ∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF
∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC,EF![]() 平面BEF,
平面BEF,
∴不论λ为何值恒有平面BEF⊥平面ABC. 6分
(2)由(Ⅰ)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC. 8分 ∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴![]() 10分
10分
![]() 由AB2=AE·AC 得
由AB2=AE·AC 得![]()
故当![]() 时,平面BEF⊥平面ACD. 12分
时,平面BEF⊥平面ACD. 12分
5、(I)解f(x)=10-f(2m-x)若m=-1,则f(x)关于(-1,5)对称. (1分)
所以a=1,![]() (3分)
(3分)
即![]() (4分)
(4分)
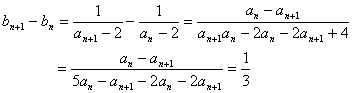
所以{bn}是以![]() 为公差的等差数列.
(6分)
为公差的等差数列.
(6分)
![]() (7分)
(7分)
所以![]() (8分)
(8分)
(II)证明:
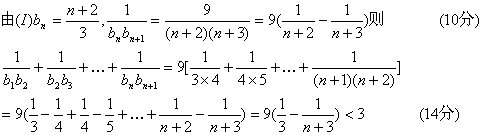
6、(1)![]() ,由已知
,由已知![]() 在[0,1]上大于等于0,在[1,2]上小于
在[0,1]上大于等于0,在[1,2]上小于
等于0.∴x=1为极大值点,![]()
(2)由![]() ,有三个相异实根,
,有三个相异实根,![]()
且![]()
(3)![]() 在[1,2]上为减函数,∴最大值为
在[1,2]上为减函数,∴最大值为![]() ,∴只有
,∴只有![]()
上恒成立即可 ![]() 恒成立,又
恒成立,又![]() ,
,
![]() 的最大值为-2,
的最大值为-2,![]()