高三数学高考冲刺阶段模拟题（一）

高三数学高考冲刺阶段模拟题（一）　　　

　　　 　 

一、选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知集合U = {1，2，3，4，5，6，7}，A = {3，4，5}，B = {1，3，6}，则A∩(_UB)等于（　A　）

A．{4，5}　　　　 B．{2，4，5，7}　　　 C．{1，6}　　　 D．{3}

2．函数f (x ) =的定义域是（　D　）

A．{x x≥－1}　　 B．{x x≥1}　　 C．{x x＞－1}　　 D．{x x＞1}

3．若指数函数y = a^x的反函数的图象经过点 (2，－1)，则a等于（　A  ）

A．　　　　　  B．2　　　　　  C．3　　　　　　　 D．10

4．在正项等比数列{a_n}中，a₁、a₉₉是方程x²－10x + 16 = 0的两个根，则a₄₀·a₅₀·a₆₀的值为（  B  ）

A．32　　　　　  B．64　　　　  C．±64　　　　　 D．256

5．若把一个函数的图象按= (－，－2)平移后得到函数y = cosx的图象，则原图象的函数解析式是（　D　）

A．y = cos (x +)－2　　　　　　　　 B．y = cos (x－)－2

C．y = cos (x +) + 2　　　　　　　　 D．y = cos (x－) + 2

6．如图，四面体P－DEF中，M是棱EF的中点，PD、PE、PF两两垂直，必有（ C　）

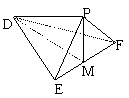A．DM⊥平面PEF

B．PM⊥平面DEF

C．平面PDE⊥平面PEF

D．平面PDE⊥平面DEF

7．若二项式 (x－)ⁿ的展开式的第5项是常数项，则正整数n的值为（ B　）

A．7　　　　  B．8　　　　 C．9　　　　　 D．10

8．4本不同的书全部分给3个同学，每人至少一本，则不同的分法有（　C ）

A．12种　　　　　　 B．24种　　　　　  C．36种　　　　　　 D．48种

二、填空题：本大题共6小题，每小题5分，共30分，把答案填在题中横线上.

9．某学校有初中生1080人，高中生900人，教师120人，现对该学校的师生进行样本容量为n的分层抽样，已知抽取的高中生为60人，则样本容量n为　　　　 .（140）

10．已知平面向量= (0，1)，= (x，y)，若⊥，则实数y = 　　　　　.（0）

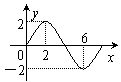11．函数f (x ) = A sin (ωx +)（A＞0，ω＞0，＜的部分图象如图所示，则f (x )的解析式为　　　　　　 .（f (x ) = 2sinx）

12．在等差数列{a_n}中，已知a₁₁ = 10，那么它的前21项的和S₂₁ = 　　　　 .（210）

13．已知m、n是直线，α、β、γ是平面，给出下列命题：① α⊥β，α∩β= m，m⊥n，则n⊥α或n⊥β；② 若α∥β，α∩γ= m，β∩γ= n，则m∥n；③ 如果直线m与平面β内的一条直线平行，那么m∥β；④ 若α∩β= m，n∥m，且nα，nβ，则n∥α且n∥β. 所有正确命题的序号是　　　　　  .（②④）

14．在密码学中，你直接可以看到的内容为明码，对明码进行某种处理后得到的内容为密码，有一种密码，将英文的26个字母a、b、c，…，z（不论大小写）依次对应1，2，3，…，26，这26个自然数，见表格：

a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	p	q	r	s	t	u	v	w	x	y	z
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26

现给出一个变换公式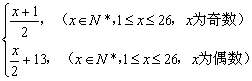：=，可将英文的明文（明码）转换成密码，按上述规定，若将某英文明文译成的密码是shxc，那么原来的明文是　　　　  .（love）

三、解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.

15．（本小题满分12分）t x

已知cos2θ=，θ∈(，π).

（I）求sinθ的值；

（II）求sin (θ+)－sin2θ的值.

解：（I）∵ cos2θ=，∴ 1－2sin²θ=，

∴ sin²θ=.

∵θ∈(，π)，∴ sinθ=.

（II）∵ sinθ=且θ∈(，π)，

∴ cosθ=，∴ sin2θ= 2sinθcosθ= 2××() =.

∴ sin (θ+)－sin2θ= sinθ·cos+ cosθ·sin－sin2θ

　　　　　　　　　　　　　　　　　 =×+ ()×－()

　　　　　　　　　　　　　　　　　 =.

16．（本小题满分14分）

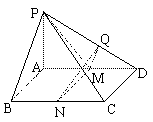已知四棱锥P－ABCD，底面是边长为1的正方形，侧棱PA⊥底面ABCD且PA = 1，M、N分别为AD、BC的中点，MQ⊥PD于Q.

（I）求证：AB∥平面MNQ；

（II）求证：平面PMN⊥平面PAD；

（III）求二面角P－MN－Q的余弦值.

解：（I）证明：∵ ABCD为正方形且M、N分别为AD、BC的中点，

∴ AB∥MN.

又∵ MN平面MNQ，AB平面MNQ，

∴ AB∥平面MNQ.

（II）证明：∵ ABCD为正方形且M、N分别为AD、BC的中点，

∴ MN⊥AD.

∵ PA⊥平面ABCD，MN平面ABCD，∴ MN⊥AP. 又∵ AD∩AP = A，

∴ MN⊥平面PAD，又∵ MN平面PMN，∴ 平面PMN⊥平面PAD.

（III）由（II）有MN⊥平面PAD，PM平面PAD，MQ平面PAD，

∴ MN⊥PM，MN⊥MQ，

∴ ∠PMQ为二面角P－MN－Q的平面角.

∵ PA = AD = 1，∴ ∠PDA =.

在Rt△MQD中，MQ =MD =，在Rt△PAM中，PM ==.

在Rt△PMQ中，cos∠PMQ ===.

∴ 二面角P－MN－Q的余弦值为.

17．（本小题满分13分）

在甲、乙两个队的乒乓球比赛中，乒乓球的规则是“五局三胜制”，现有甲、乙两队每局获胜的概率分别为和.

（I）前两局乙队以2：0领先，求最后甲、乙两队各自获胜的概率；

（II）乙队以3：2获胜的概率.

解：（I）在乙队以2：0领先的前提下，若甲队获胜则第三、四、五局均为甲队取胜，所以甲队获胜的概率为P₁ = ()³ =.

（方法1）在乙队以2：0领先的前提下，若乙队获胜则乙队可能以3：0；3：1；3：2的比分赢得比赛，所以乙队获胜的概率为：

　　　　　　　　P₂ =+×+ ()²×=.

（方法2）“甲队获胜”与“乙队获胜”为对立事件，所以乙队获胜的概率为：

　　　　　　　　P₂ = 1－=.

（II）若乙队以3：2获胜，则第五局为乙队取胜，前四局乙队输两局赢两局，所以乙队以3：2获胜的概率为：

　　　　　　　　P₃ =·()²·()²·=.

18．（本小题满分13分）

已知函数f (x ) = x² (ax + b )（a，b∈R）在x = 2时有极值，其图象在点 (1，f (1 ))处的切线与直线3x + y = 0平行.

（I）求a、b的值；

（II）求函数f (x )的单调区间.

解：（I）∵f (x ) = x² (ax + b ) = ax³ + bx²，

∴(x ) = 3ax² + 2bx，∵ 函数f (x )在x = 2时有极值，

∴ (2 ) = 0，即 12a + 4b = 0，　　　　　　　　　　　　　　　①

∵ 函数f (x )的图象在点(1，f (1 ))处的切线与直线3x + y = 0平行.

∴ (1 ) =－3，即3a + 2b =－3，　　　　　　　　　　　　　　 ②

由①②解得，a = 1，b =－3.

（II）(x ) = 3x²－6x = 3x (x－2)，令3x (x－2)＞0，

解得：x＜0或x＞2，

令3x (x－2)＜0，解得：0＜x＜2.

∴ 函数f (x )的单调递增区间为(－∞，0)和(2，+∞)，单调递减区间为(0，2).

19．（本小题满分14分）

设数列{a_n}满足a₁ = 2，a_{n +1} = 3a_n－2，n = 1，2，3，….

（I）求证：数列{a_n－1}是等比数列；

（II）求{a_n}的通项公式；

（III）求{a_n}的前n项和S_n.

解：（I）证明：∵ a_{n +1} = 3a_n－2，且a₁ = 2，

∴ a_{n +1}－1 = 3 (a_n－1)，且a_n≠1，

∴ = 3，∴数列{a_n－1}是等比数列.

（II）∵数列{a_n－1}是等比数列，

∴ a_n－1 = (a₁－1)·q^n－1 = (2－1)·3^n－1 = 3^n－1，

∴ a_n = 3^n－1 + 1.

∴ {a_n}的通项公式a_n = 3^n－1 + 1.

（III）S_n = a₁ + a₂ + a₃ + … + a_n

　　　　　　　 = (3⁰ + 1) + (3 + 1) + (3² + 1) + … + (3^n－1 + 1)

　　　　　　　 = (3⁰ + 3 + 3² + … + 3^n－1 ) + n

　　　　　　　 =+ n =×3ⁿ + n－.

20．（本小题满分14分）

已知函数f (x) = x x－a （a∈R）.

（I）判断f (x )的奇偶性；

（II）解关于x的不等式：f (x )≥2a²；

（III）写出f (x )的单调区间.

解：（I）函数f (x )的定义域是R，当a = 0时，f (－x ) =－x －x =－x x =－f (x )，

∴ f (x )是奇函数.

当a≠0时，∵ f (a ) = 0，f (－a ) = －2a a ，

∴ f (－a )≠f (a )且f (－a )≠－f (a )，

∴ f (x )既不是奇函数，也不是偶函数.

（II）∵ x x－a ≥2a²，

∴ 原不等式等价于　　①　或　　 ②

由①得，无解；

由②得，即，

⑴ 当a = 0时，x≥0；

⑵ 当a＞0时，由，得x≥2a.

⑶当a＜0时，由，得x≥－a.

综上，当a≥0时，f (x )≥2a²的解集为{x x≥2a}；当a＜0时，f (x )≥2a²的解集为{x x≥－a}.

（III）f (x) = x x－a =.

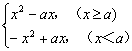⑴ a = 0时，如图1，函数f (x )在R上为单调递增函数，(－∞，+∞)为单调递增区间；

⑵ a＞0时，如图2，函数f (x )的单调递增区间为[a，+∞和－∞，]，单调递减区间为[，a]；

⑶ a＜0时，如图3，函数f (x )的单调递增区间为[，+∞和－∞，a]，单调递减区间为[a，].