2006年高考理科数学摸拟试题解析样本5
本试卷分第Ⅰ卷(选择题 共60分)和第Ⅱ卷(非选择题 共90分)，考试时间为120分钟，满分为150分.
第Ⅰ卷 (选择题 共60分)
一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1.集合A={xx=2k,k∈Z},B={xx=2k+1,k∈Z},C={xx=4k+1,k∈Z},又a∈A,b∈B,则有
A.a+b∈A
B.a+b∈B
C.a+b∈C
D.a+b不属于A，B，C中的任意一个
2.已知f(x)=sin(x+
,g(x)=cos(x－),则f(x)的图象
A.与g(x)的图象相同
B.与g(x)的图象关于y轴对称
C.向左平移个单位，得到g(x)的图象
D.向右平移个单位，得到g(x)的图象
3.过原点的直线与圆x2+y2+4x+3=0相切，若切点在第三象限，则该直线的方程是
A.y=
x B.y=－x
C.y=
x D.y=－x
4.函数y=1－
, 则下列说法正确的是
A.y在(－1,+∞)内单调递增 B.y在(－1,+∞)内单调递减
C.y在(1,+∞)内单调递增 D.y在(1,+∞)内单调递减
5.已知直线m,n和平面
，那么m∥n的一个必要但非充分条件是
A.m∥,n∥ B.m⊥,n⊥
C.m∥且n
D.m,n与成等角
6.在100个零件中，有一级品20个，二级品30个，三级品50个，从中抽取20个作为样本：①采用随机抽样法，将零件编号为00，01，02，…，99，抽出20个；②采用系统抽样法，将所有零件分成20组，每组5个，然后每组中随机抽取1个；③采用分层抽样法，随机从一级品中抽取4个，二级品中抽取6个，三级品中抽取10个；则
A.不论采取哪种抽样方法，这100个零件中每个被抽到的概率都是
B.①②两种抽样方法，这100个零件中每个被抽到的概率都是，③并非如此
C.①③两种抽样方法，这100个零件中每个被抽到的概率都是，②并非如此
D.采用不同的抽样方法，这100个零件中每个被抽到的概率各不相同
7.曲线y=x3在点P处的切线斜率为k，当k=3时的P点坐标为
A.(－2,－8) B.(－1,－1),(1,1)
C.(2,8) D.(－
,－
)
8.已知y=loga(2－ax)在［0，1］上是x的减函数，则a的取值范围是
A.(0，1) B.(1，2)
C.(0，2) D.［2，+∞
9.已知lg3,lg(sinx－),lg(1－y)顺次成等差数列，则
A.y有最小值
，无最大值 B.y有最大值1，无最小值
C.y有最小值，最大值1 D.y有最小值－1，最大值1
10.若
=a，
=b，则∠AOB平分线上的向量
为
A.
B.
()，由决定
C.
D.
11.一对共轭双曲线的离心率分别是e1和e2,则e1+e2的最小值为
A.
B.2
C.2 D.4
12.式子
的值为
A.0 B.1
C.2 D.3
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中横线上)
13.从A={a1,a2,a3,a4}到B={b1,b2,b3,b4}的一一映射中，限定a1的象不能是b1，且b4的原象不能是a4的映射有___________个.
14.椭圆5x2－ky2=5的一个焦点是(0，2)，那么k=___________.
15.已知无穷等比数列首项为2，公比为负数，各项和为S，则S的取值范围为___________.
16.已知an是(1+x)n的展开式中x2的系数，则
=___________.
三、解答题(本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知函数f(x)=
，记数列{an}的前n项和为Sn，且有a1=f(1),当n≥2时，Sn－
(n2+5n－2).
(1)计算a1，a2，a3，a4;
(2)求出数列{an}的通项公式，并给予证明.
18.(本小题满分12分)
已知△ABC的三个内角A，B，C，满足sinC=
.
(1)判断△ABC的形状；
(2)设三边a,b,c成等差数列且S△ABC=6 cm2，求△ABC三边的长.
19.(本小题满分12分)
如图，矩形ABCD与ADQP所在平面垂直，将矩形ADQP沿PD对折，使得翻折后点Q落在BC上，设AB=1，PA=h，AD=y.
(1)试求y关于h的函数解析式；
(2)当y取最小值时，指出点Q的位置，并求出此时AD与平面PDQ所成的角；
(3)在条件(2)下，求三棱锥P—ADQ内切球的半径.
20.(本小题满分12分)
某人上午7时，乘摩托艇以匀速v海里/时(4≤v≤20)从A港出发到距50海里的B港去，然后乘汽车以w千米/时(30≤w≤100)自B港向距300千米的C市驶去，应该在同一天下午4至9点到达C市.设汽车、摩托艇所需的时间分别是x、y小时.
(1)作图表示满足上述条件x、y的范围；
(2)如果已知所需的经费p=100+3(5－x)+2(8－y)(元)，那么v、w分别是多少时走得最经济？此时需花费多少元？
21.(本小题满分12分)
已知f(x)=loga(x+1)，点P是函数y=f(x)图象上的任意一点，点P关于原点的对称点Q的轨迹是函数y=g(x)的图象，当a＞1,x∈［0,1时，总有2f(x)+g(x)≥m恒成立.
(1)求出g(x)的表达式；
(2)求m的取值范围.
22.(本小题满分14分)
直线l:ax－y－1=0与曲线C：x2－2y2=1交于P、Q两点，
(1)当实数a为何值时，PQ=2
?
(2)是否存在a的值，使得以PQ为直径的圆经过原点？若存在，求出a的值；若不存在，说明理由.
参考答案
一、选择题(每小题5分，共60分)
1.解析：由已知得a是偶数，b是奇数，则a+b是奇数，又b∈B，B
C，∴a+b∈B,选B.
答案：B
2.解析：f(x)的图象向右平移个单位，得sin［(x－)+］=sinx，又g(x)=cos(x－=cos(－x)=sinx,故选D.
答案：D
3.解析：设直线为y=kx.
由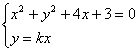
消去y，得
(1+k2)x2+4x+3=0,
由Δ=16－4×3(1+k2)=0,k=±.
又知切点在第三象限，∴k=，选C.
答案：C
4.解析：令x－1=X,y－1=Y,则Y=－
.
X∈(0,+∞)是单调增函数，由X=x－1,得x∈(1,+∞)，y=1－为单调增函数,故选C.
答案：C
5.解析：若m∥n,则m,n与平面成相等的角，反之 ，若m,n与平面成等角，不一定有m∥n,故选D.
答案：D
6.解析：将三种抽样法的有关计算公式计算所得的概率都是，故选A.
答案：A
7.解析：由y=x3，得y′=3x2.由已知得3x2=3，x=±1.
当x=1时，y=1,当x=－1时，y=－1，
故P点的坐标为(1，1)或(－1，－1)，选B.
答案：B
8.解析：由已知loga(2－a·0)＞loga(2－a)，即loga2＞loga(2－a)，
当0＜a＜1时，有
无解，
当a＞1时，有
，得1＜a＜2,选B.
答案：B
9.解析：由已知得2lg(sinx－)=lg3+lg(1－y)，且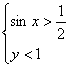
,
得(sinx－)2=3(1－y)
得y=1－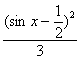
,
当sinx=1时，ymin=，无最大值，选A.
答案：A
10.答案：B
11.解析：设双曲线
=1的离心率e1=
，
则共轭双曲线
=1的离心率e2=
.
e1+e2=
≥2·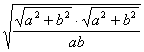
(a=b时取等号)
=2·
≥2· (a=b时取等号).
∴e1+e2的最小值为2，选C.
答案：C
12.解析：原式=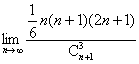
=
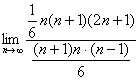=2,选C.
答案：C
二、填空题(每小题4分，共16分)
13.解析：A
－2A
+A
=14.
答案：14
14.解析：由已知得x2+
=1,k＜0,
由焦点坐标(0，2)知长轴在y轴上，
得(－
)－1=4,得k=－1.
答案：－1
15.解析：由题意得S=
,－1＜q＜0.
由q=
得－1＜＜0,解不等式得1＜S＜2.
答案：1＜S＜2
16.解析：由已知得x2的系数为C
，即an=C=
,
∴a2=1,
=1=
,
,…,
,
∴
=
.
答案：2
三、解答题(17、18、19、20、21题，每题12分，22题14分，共74分)
17.解：(1)由已知，当n≥2时，f(an)=
,
∵Sn－
，
∴Sn－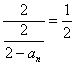
(n2+5n－2),
即Sn+an=(n2+5n+2).
又a1=f(1)=2,
由S2+a2=a1+2a2=(22+5×2+2),
得a2=3;
由S3+a3=a1+a2+2a3=(32+5×3+2),
解得a3=4;
由S4+a4=a1+a2+a3+2a4=(42+5×4+2),解得a4=5. 6分
(2)则a1=2,a2=3,a3=4,a4=5,于是猜想：an=n+1(n∈N). 8分
以下用数学归纳法证明：
(a)当n=1时命题成立.
(b)设n=k时，ak=k+1(k∈N).
由Sk+1+ak+1=［(k+1)2+5(k+1)+2］,
a1+a2+…+ak+2ak+1=(k2+7k+8),
2ak+1=(k2+7k+8)－(2+3+…+k+1)
=(k2+7k+8)－
=(k2+7k+8－k2－3k)
=2k+4.
ak+1=(k+1)+1,
即当n=k+1时命题也成立.
故由(a)、(b)知对一切n∈N均有an=n+1. 12分
18.(1)解法一：sinC=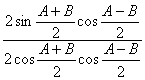
=tan
=
.
∵sinC≠0,∴cosC=0,0°＜C＜180°,
∴C=90°,∴△ABC为直角三角形. 6分
解法二：∵cosA+cosB=
,
∴
.
化简整理得：(a+b)(c2－a2－b2)=0,∴a2+b2=c2,
∴△ABC为直角三角形. 6分
(2)解：由已知得：a2+b2=c2,a+c=2b,ab=6,
解得：a=3 cm,b=4 cm,c=5 cm. 12分
19.解：(1)显然h＞1，连接AQ，
∵平面ABCD⊥平面ADQP,PA⊥AD，
∴PA⊥平面ABCD，由已知PQ⊥DQ,
∴AQ⊥DQ,AQ=y2－h2.
∵Rt△ABQ∽Rt△QCD,CQ=
,
∴
,即
.
∴y=
(h＞1). 4分
(2)y==
=+
≥2, 6分
当且仅当
,即h=时，等号成立.
此时CQ=1,即Q为BC的中点，于是由DQ⊥平面PAQ，知平面PDQ⊥平面PAQ,PQ是其交线，则过A作AE⊥平面PDQ,∴∠ADE就是AD与平面PDQ所成的角，由已知得AQ=,PQ=AD=2,∴AE=1,sinADE=
,∠ADE=30°. 8分
(3)设三棱锥P－ADQ的内切球半径为r,
则
(S△PAD+S△PAQ+S△PDQ+S△ADQ)·r=VP－ADQ .
∵VP－ADQ=S△ADQ·PA=
,S△PAQ=1,
S△PAD=,S△QAD=1,S△PDQ=,
∴r=
. 12分
20.解：(1)由题意得：v=
,w=
,4≤v≤20,30≤w≤100, 3分
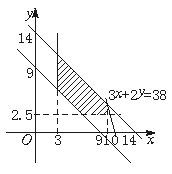
∴3≤x≤10,
≤y≤
.①
由于汽车、摩托艇所要的时间和x+y应在9至14小时之间，即9≤x+y≤14,②
因此满足①②的点(x,y)的存在范围是图中阴影部分(包括边界). 6分
(2)因为p=100+3(5－x)+2(8－y),所以3x+2y=131－p,设131－p=k,那么当k最大时，p最小，在图中通过阴影部分区域且斜率为－
的直线3x+2y=k中，使k值最大的直线必通过点(10,4)，即当y=4时，p最小，此时x=10,v=12.5,w=30,p的最小值为93元. 12分
21.解：(1)设Q(x,y)
P(－x,－y),代入f(x)方程得，g(x)=－loga(－x+1). 4分
(2)2f(x)+g(x)≥m恒成立
2loga(x+1)－loga(1－x)≥m恒成立
loga
≥m恒成立,即m小于等于loga的最小值.
令h(x)=
=
. 8分
易证h(x)在x∈［0,1)上单调递增，
∴h(x)min=h(0)=1,
又∵a＞1,∴loga≥loga1=0,
即loga的最小值为0，
∴m的取值范围是m≤0. 12分
22.解：(1)设P(x1,y1),Q(x2,y2),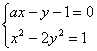
,
∴(1－2a2)x2+4ax－3=0.
若1－2a2=0,即a=±
时，l与C的渐近线平行，l与C只有一个交点，与题意不合，
∴1－2a2≠0,Δ=(4a)2－4(1－2a2)(－3)＞0,
∴－
＜a＜.
(*)
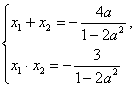∴｜PQ｜=｜x1－x2｜=2.
∴(x1－x2)2=4,∴(x1+x2)2－4x1x2=4.
∴(－
)2－4
=4.
∴a=±1∈(－,).
∴所求的实数a的值为a=±1. 5分
(2)假设存在实数a,使得以PQ为直径的圆经过原点O，则由OP⊥OQ，得y1·y2=－x1·x2.
∴(ax1－1)·(ax2－1)=－x1·x2,
∴(1+a2)x1·x2－a(x1+x2)+1=0. 9分
把(*)式代入得：a2=－2与a为实数矛盾，
∴不存在实数a使得以PQ为直径的圆经过原点. 14分