“3+X”高考知名重点中学双向抽测冲刺数学试卷

2005年“3+X”高考知名重点中学双向抽测冲刺试卷

数　学

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分。考试时间120分钟。

第Ⅰ卷（选择题共60分）

一、选择题（每小题5分，共60分）

1．设全集为R，M = {x f (x) ≠ 0}，N = {x g(x) ≠0}.则集合{x f（x）·g（x）= 0}= （　　）

　 A．M∪N　　　　  B．M∩N　　　 　 C．M∪N　　　　　 D．M∩N

2．函数f (x) = x - 3 - x - 1，x∈R，则f（x）　　　 （　　）

　 A．有最小值0，最大值4　　　　　　  B．有最小值-4，最大值0

　 C．有最小值-4，最大值4　　　　　　  D．没有最小值及最大值

3．已知a＞0，b＞0，且a + b = 1，若a² + b²≥k，则k的最大值是　（　　）

　 A．1　　　　　　  B．　　　　　　 C．　　　 　　　 D．

4．已知f （cos x）= cos 2x，则f (sin) =　　　　 （　　）

　 A．　　　　　 B．-　　　　　 C．　　　　　　  D．-

5．双曲线的两条渐近线的夹角为，则其离心率为　　（　　）

　 A．sec　　　　  B．tg　　　　　 C．tg或ctg　 D．sec或csc

6．定义在（-∞, +∞）上的函数f（x）在（-∞，2）上是增函数，且函数f（x+2）为偶函数，则　（　　）

　 A．f（-1）＜ f （3）　　　　　　　　  B．f（0）＞ f （3）

　 C．f（-1）= f （-3）　　　　　　　　　 D．f（2）＜ f （3）

7．正方体ABCD – A₁B₁C₁D₁中，E、F、G分别是AB、BC、CC₁的中点，则过E、F、G的截面与底面ABCD所成二面角的正切值是　（　　）

　 A．　　　　  B．　　　　　　 C．1　 　　　　　　D．

8．设{a_n}是正数组成的等差数列，{b_n}是正数组成的等比数列，且a₁ = b₁，a_2n+1 = b_2n+1,则有　 （　　）

　 A．a_n+1≥b_n+1　　　　　　　　　　　　  B．a_n+1≤b_n+1

　 C．a_n+1＞b_n+1　　　　　　　　　　　　  D．a_n+1＜b_n+1

9．设集合A = {z z = i^5k-4，0＜k≤8且k∈N}，则A中所有元素之和为　 （　　）

　 A．0　　　　　　 B．1　　　　　　　  C．-1　　　　　　  D．4i

10．方程表示焦点y轴上的椭圆，则m的取值范围是　（　　）

　　A．m＜2　　　　　　　　　　　　　　  B．1＜m＜2　　　　 

C．m＜-1或1＜m＜2　　　　　　　　　 D．m＜-1或1＜m＜

11．由父母及孩子组成的两个三口之家要分乘两辆小轿车外出游，每辆车最多只能乘坐4人，其中两个小孩不能单独坐同一辆车，则不同的乘车方法共有　（　　）

A．40种　　　　　 B．48种　　　　　 C．60种　　　　　 D．68种

12．某产品的总成本y（万元）与产量x（台）之间的函数关系是y = 3000 + 20x - 0.1x²，

其中0＜x＜240，x∈N，若每台产品的售价为25万元，则生产不亏本（销售收入不小于总成本）的最低产量是　（　　）

A．100台　　　　  B．120台　 　　　 C．150台　　　　  D．180台

第Ⅱ卷（非选择题共90分）

二、填空题（每小题4分，共16分）

13．函数y = 的最大值是____________。

14．正三棱锥S – ABC中，E为SA中点，F是△ABC的中点，且SA = BC，则直线EF与直线AB所成角的度数为___________。

15．过抛物线y² = 8x焦点的弦AB长为12，设A（x₁，y₁），B（x₂，y₂），则x₁+x₂=_______。

16．已知a、b是常数，lim，则下面四个命题：①3^a＜3^b　 ②a³＜b³   ③a²＜b²　 ④lga＜lgb，恒成立的题号是____________。

三、解答题（共6题，总分74分）

17．已知复数 z = 1，且z² +2z +＜0，求复数z。（本题12分）

18．定义在R上的函数f（x）对任意实数a、b都有f（a + b）+ f（a - b）= 2f（a）·f（b）成立，且f（0）≠0。

　　（1）求f（0）;

　　（2）证明f（x）的奇偶性；

　　（3）若存在常数c＞0使f（）=0，试问f（x）是否为周期函数。若是，指出它的一个周期，若不是请说明理由。（本题12分）。

19．已知△ABC的三个内角A、B、C成等差数列，且A＜B＜C，tg A·tg C = 2+。

　　（1）求角A、B、C的大小；

　　（2）如果BC边长为4，求△ABC的AC边长及三角形的面积。（本题12分）

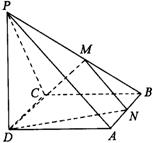
20．已知四棱锥P - ABCD 的底面是边长为4的正方形，PD⊥底面ABCD，PD = 6，M、N分别是PB、AB的中点。

　　（1）求证：MN⊥CD；

　　（2）求三棱锥P – DMN 的体积；

　　（3）求二面角M – DN – C的平面角的正切值。（本题13分）

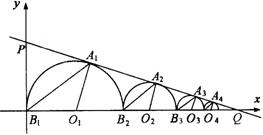
21．直线PQ的方程为3x + 4y – 4 = 0，半圆O₁、O₂、… O_n、…依次外切且都与直线PQ相切，其中圆O₁与y轴相切，圆心O₁、O₂，… O_n …都在x轴正半轴上，设它们的半径依次为r₁、r₂、…、r_n…，与直线PQ的切点依次为A₁、A₂、…A_n、…。

　　（1）求这一系列半圆半径组成的无穷数列{ r_n }的通项公式r_n；

　　（2）求这一系列三角形A₁O₁B₁、A₂O₂B₂，…，A_nO_nB_n…的面积之和.（本题12分）

22．抛物线C的方程为y² = p（x + 1），其中p＞0，直线l：x + y = m与x轴的交点在抛物线准线的右侧。

　　（1）求证l与C总有两个交点；

　　（2）若l与C的交点为Q、R，且OR⊥OQ（O为原点），求用m表示p的函数p = f（m）；

　　（3）在条件（2）下，若m变化，使得O到l的距离不大于，求p的取值范围。（本题13分）

数 学 参 考 答 案

1　　　　　 选择题

1．C　2．C　3．B　4．B　5．D　6．A　7．D　8．A　9．A　10．D　11．B　12．C

二、填空题

13．　14．60°　15．8　16．①、③

三、解答题

17．设z = a + bi(a，bR)，则a² + b² = 1.　　　　  （1分）

　　由z² + 2z + ＜0

　　∴（a² – b² + 2abi）+ 2（a+bi）+＜0　　　 （2分）

∴（a² – b² + 3a）+（2ab+b）i＜0　　　 （4分）

∴　　　　　　　　　　　  （6分）

由②得b = 0或a = –

当b = 0时，由a² + b² = 1得a² = 1,代入①得　　　 （8分）

1+3a＜0，a＜–　　　　（9分）

当a = –时，由a² + b² = 1得b² = ，代入①得

b²＞–　　　　  （11分）

综上，z = –1或z = –i.　　　 （12分）

18．（1）令a = b = 0得f (0)+ f (0) = 2f (0)·f (0)　　　　 （2分）

　　　　∴f (0)·[f (0)–1] = 0，∵f (0)≠0

∴f (0) =1.　　　 （4分）

（2）令a = 0，b = x得f (x) + f (–x) = 2 f (0)·f (x)　　　　 （5分）

　　 由f (0) = 1，∴ f (–x) = f (x).　　　　 　 （7分）

　　 ∴f (x)是R上的偶函数.　　　　（8分）

（3）令a = x +  得

　　 f [（x +）+]+f [(x +)–] = 2f (x +)·f ()　　　（9分）

　　由f（）=0

　　∴f (x+c)+f (x) = 0　　　　 （10分）

　 ∴f (x+c) = –f (x)

　 ∴f (x +2c) = –f (x+c) = –〔–f（x）〕=f (x)　　　　 （11分）

　　 ∴f (x)是以2c为周期的周期函数.　　　 （12分）

19．（1）∵A、B、C成等差数列，∴A+B = 2B.　　　

∵A+B+C = 3B =，∴B =，A+C =.　　　　 （1分）

∵tg A + tg C = tg（A+C）（1– tg A·tg C）= tg

（3分）

∴　　　　　　　　  　　　　　　或　　　　　 .

　　 由A＜C知tg A＜tg C

　　 ∴tg A = 1，tg C = 2 +　　　　  （5分）

　　 即A =

　　 故A = ，B = ，C = .　　　　　　 （6分）

（2）由正弦定理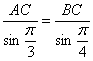

　　 ∴AC = 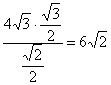　　　　　　 （8分）

　　 由S_△ABC= AC·BC·sin C

　　　　　　 =×675°　　　　 （9分）

　　　　　　 =12·sin（45°+30°）　　　　  （11分）

　　　　　　 =18+6.

　　 故AC =6，S_△ABC = 18 + 6.　　　　　  （12分）

20．（1）∵PD⊥底面ABCD，∴PD⊥CD.　　　　　　 （1分）

∵CD⊥DA，∴ CD⊥平面PDA.

∴CD⊥PA.　　　　　  （2分）

∵M、N是PB、AB中点，∴MN∥PA.

∴MN⊥CD.　　　　　 （4分）

　　　　  （2）设AC、BD交于O，连结MO、PN.

∴V_P–DMN = V_A–DMN = V_M–ADN　　　　　 （6分）

∵M是PB中点，∴M到平面ABCD的距离等于，S_△ADN =S_□ABCD.∴V_M–ADN =_□ABCD×.

∴V_P–DMN = 4.　　　　　  （8分）

　　　　  （3）过O点向DN作垂线OK，K为垂足，连结OM，则OM⊥DN，∠OKM为二面角M – DN – C的平面角.　　　　　 （9分）

　　　　　　   在Rt△NOK中

　　　　　　　 OK = ON·sin∠OND = ON·sin∠ADN = 　　　　 （11分）

　　　　　　　 在Rt△MOK中

　　　　　　　 tg∠OKM = 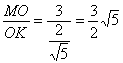.　　　　　 （12分）

　　　　　　　 ∴二面角M – DN – C 的平面角正切值为.　　　　  （13分）

　　21．（1）由点O_n+1向半径O_nA_n作垂线，设垂足为C_n.

　　　　　  ∴O_nC_n=r_n–r_n+1, O_nO_n+1 = r_n + r_n+1,且有∠C_nO_n+1O_n =∠PQB₁　　　（1分）

　　　　　  由直线PQ方程3x + 4y – 4 = 0可得

　　　　　  B₁P = 1， B₁Q = .　　　 （2分）

　　　　　  在△C_nQ_n+1Q_n中，sin∠C_nO_n+1O_n .整理得

　　　　　  ∴{r_n}是公比为的等比数列.　　　　　　  （4分）

　　　　　  由△A₁O₁Q ~△B₁PQ，

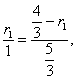　　　　　  ∴解出r₁ = .　　　　（5分）

　　　　　  ∴r_n =×（）.　　　　　 （6分）

　　　 （2）在第n个△A_nO_nB_n中，∠ A_nO_nB_n +∠B₁PQ = .

　　　　　  sin∠B₁PQ=cos∠PQB₁ =　　　　　  （8分）

　　　　　  ∴S

　　　　　  =

　　　　  　=.　　　　（10分）

　　　　　  图中一系列三角形的面积组成以为首项，为公比的无穷等比递缩数列，其各项之和为

　　　　　  S = lim S_n = 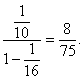　　　　　　（12分）

　　22．（1）由　　　　  得x² –（2m + p）x + m² – p = 0　　　　 （1分）

　　　　　  抛物线准线为x = –1–，l与x轴交点为（m，0）.

　　　　　  ∴m＞–1–，即4m + p +4＞0.　　　　　 （2分）

　　　　　  由p＞0知方程x²–（2m+p）x+m² – p = 0的判别式

　　　　　　  △= p（4m + p + 4）＞0恒成立.

　　　　　  ∴l与c总有两个交点.　　　　　　 （4分）

　　　 （2）设Q（x₁，y₁）、R(x₂，y₂).

　　　　　  ∵OQ⊥OR，∴ x₁x₂ + y₁y₂ = 0.　　　　　  （5分）

　　　　　  且x₁+x₂ = 2m+p，x₁·x₂ = m²–p.　　　　  （6分）

　　　　　  ∴x₁x₂ + y₁y₂ = x₁x₂ + (m–x₁)(m–x₂)

　　　　　　　　　　　 = 2x₁x₂ – m(x₁+x₂)+m²

　　　　　　  　　　　 = 2(m²–p)–m(2m+P)+m² = 0　　　　　  （8分）

　　　　　  ∴p = f（m）=.　

　　　　　  由p＞0知m＞–2且m≠0.　　　　  （9分）

　　　 （3）设原点O到l距离为d.

　　　　　  则d = ≤ 即 m ≤1　　　 （10分）

　　　　　  ∴m[–1，0　∪（0，1　（11分）

　　　　　  p = 　　　　　　　（12分）

　　　　　 由（–∞，–1∪[1，+∞

　　　　　 得0＜p≤1.　　　　　 （13分）