素质能力检测（一）
一、选择题（每小题5分，共60分）
1.（2004年北京，1）设全集是实数集R，M={x－2≤x≤2}，N={xx＜1}，则
∩N等于
A.{xx＜－2} B.{x－2＜x＜1}
C.{xx＜1} D.{x－2≤x＜1}
解析：∵=｛xx＜－2或x＞2｝，∴∩N=｛x｜x＜－2｝.
答案：A
2.下列四个命题，其中正确命题的个数为
①与1非常接近的全体实数能构成集合 ②{－1，（－1）2}表示一个集合 ③空集是任何一个集合的真子集 ④任何两个非空集合必有两个以上的子集
A.0 B.1 C.2 D.3
解析：命题②④正确.
答案：C
3.设M={1，2，m2－3m－1}，P={－1，3}，M∩P={3}，则m的值为
A.4 B.－1 C.1，－4 D.4，－1
解析：∵M∩P={3}，∴3∈M.
∴m2－3m－1=3.∴m＝4或m=－1.
答案：D
4.（2005年启东市高三年级第二次调研考试）已知集合A={xx=
，k∈N}，B={xx≤4，x∈Q}，则A∩B为
A.{0，3} B.{1，3}
C.{1，4} D.{1，2，3，4}
解析：由≤4，得2k≤15，k≤7.5.又k∈N，∴k∈{0，1，2，3，4，5，6，7}.又只有k=0或k=4时能使x∈Q，∴A∩B={1，3}.
答案：B
5.（2003年合肥模拟题）给出命题p:3≥3，q:函数f（x）=
在R上是连续函数，则在下列三个复合命题“p且q”“p或q”“非p”中，真命题的个数为
A.0 B.1 C.2 D.3
解析：p真q假.
答案：B
6.已知数列{an}，那么“对任意的n∈N*，点Pn（n，an）都在直线y=2x+1上”是“{an}为等差数列”的
A.必要而不充分条件 B.充分而不必要条件
C.充要条件 D.既不充分也不必要条件
解析：点Pn（n，an）都在直线y=2x+1上，即an=2n+1.
∴{an}为等差数列，但是{an}是等差数列却不一定就是an=2n+1.
∴是充分不必要条件.
答案：B
7.如果命题“p或q”是真命题，命题“p且q”是假命题，那么
A.命题p和命题q都是假命题 B.命题p和命题q都是真命题
C.命题p和命题“非q”真值不同 D.命题p和命题“非q”真值相同
解析：p或q中有一个真命题，一个假命题.
答案：D
8.“a＞2且b＞2”是“a+b＞4且ab＞4”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析：当a=3，b=
时，满足a+b＞4且ab＞4，但不满足a＞2且b＞2.
答案：A
9.（2003年上海高考）设a1、b1、c1、a2、b2、c2均为非零实数，不等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0的解集分别为集合M和N，那么“
”是“M=N”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
解析：设=k，
则a1=ka2，b1=kb2，c1=kc2.
则a1x2+b1x+c1＞0变为ka2x2+kb2x+kc2＞0.
当k＞0时，M=N；当k＜0时，M≠N.
当M=N时，.
当M、N都为空集时，是既不充分又不必要条件.
答案：D
10.（2005年海淀区高三第一学期期末练习题）设集合A={（x，y）y=2sin2x}，集合B={（x，y）y=x}，则
A.A∩B中有3个元素 B.A∩B中有1个元素
C.A∩B中有2个元素 D.A∪B=R
解析：由图象知y=2sin2x与y=x有3个交点，因此，A∩B中有3个元素.
答案：A
11.设集合M={xx=3m+1，m∈Z}，N={yy=3n+2，n∈Z}，若x0∈M，y0∈N，则x0y0与集合M、N的关系是
A.x0y0∈M B.x0y0
M C.x0y0∈N D.x0y0N
解析：由（3m+1）（3n+2）=9mn+6m+3n+2=3（3mn+2m+n）+2，
∵m、n∈Z，∴3mn+2m+n∈Z.
∴（3m+1）（3n+2）∈N.
答案：C
12.下列四个命题中，与命题A
B等价的共有
①A∩B=A ②A∪B=B ③A∩（
UB）=
④A∪B=U
A.1个 B.2个 C.3个 D.4个
解析：如下图，知命题①②③与AB等价.
答案：C
二、填空题（每小题4分，共16分）
13.已知集合A＝{xx2+3x－10＜0}，B={xx=y+1，y∈A}，则A∩B=___________________.
解析：A={x－5＜x＜2}，B={x－4＜x＜3}.
答案：{x－4＜x＜2}
14.（2005年启东市高三年级第一次调研考试）已知A={（x，y）y=－
x+m，m∈R}，B={（x，y）
θ∈（0，2π）}，若A∩B={（cosθ1，sinθ1），（cosθ2，sinθ2）}，则m的取值范围为___________________.
解析：运用数形结合.由于集合A中的点集是平行直线系x+y－m=0，集合B中的点集是以原点为圆心，以1为半径的圆〔除去点（1，0）〕，由题意知直线与圆有两个不同交点，∴由点到直线的距离小于半径得－2＜m＜2且m≠.
答案：－2＜m＜2且m≠
15.（2005年春季上海，10）若集合A={x3cos2πx=3x，x∈R}，B={yy2=1，y∈R}，则A∩B=___________________.
解析：把集合A、B分别化简为A={x3cos2πx=3x，x∈R}={x3cos2πx=3x，x≤1}，B={－1，1}.但x=－1时，3cos（－2π）=3cos2π=3≠3－1，即－1A.∴A∩B={1}.
答案：{1}
16.已知集合A={（x，y）x+y=a，a＞0}，B={（x，y）xy+1=x+y}，若A∩B是平面上正八边形的顶点所构成的集合，则a的值是___________.
解析：集合B是直线x=±1或y=±1上的点，而集合A是由直线x+y=±a，x－y=±a围成的正方形上的点.
由题意易得a=2+
.
答案：2+
三、解答题（本大题共6小题，共74分）
17.（12分）已知A={xx2－4x－5＞0}，B={xx－a＜4}，且A∪B=R，求实数a取值的集合.
解：A={xx＞5或x＜－1}，B={xa－4＜x＜a+4}.
为使A∪B=R，∴
1＜a＜3.
18.（12分）已知M={2，3，m2+4m+2}，P={0，7，m2+4m－2，2－m}，满足M∩P={3，7}，求实数m的值和集合P.
解：∵M∩P＝{3，7}，∴7∈M，
即m2+4m+2=7.∴m=－5或m=1.
当m=－5时，M={2，3，7}，P={0，7，3，7}，P中元素不满足互异性，∴m=－5舍去.
当m=1时，M={2，3，7}，P={0，7，3，1}，满足条件，∴m=1.此时P＝{0，7，3，1}.
19.（12分）已知a＞0，求证：x2＞a的充要条件是x＞
.
证明：（1）充分性：因为x＞＞0，
所以x2=xx＞·，即x2＞a.
（2）必要性：因为x2＞a，a＞0，
所以x＜－或x＞.
当x＜－时，x＜0，从而有x=－x，
所以－x＜－，即x＞.
当x＞时，x＞0，从而有x=x，所以x＞.总之恒有x＞.
20.（12分）对于集合A={xx2－2ax+4a－3=0}，B={xx2－2ax+a+2=0}，是否存在实数a，使A∪B=？若a不存在，请说明理由；若a存在，求出a.
解：∵A∪B=，∴A=且B=.
∴
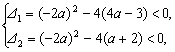
即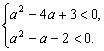
解得1＜a＜2.
∴存在实数a，满足A∪B=，此时1＜a＜2.
21.有点难度哟！
（12分）已知A={x1＜x－2＜2}，B={xx2－（a+1）x+a＜0}，且A∩B≠，试确定a的取值范围.
解：A={x0＜x＜1或3＜x＜4}.
（1）当a＞1时，B={x1＜x＜a}，
由A∩B≠，得a＞3.
（2）当a＜1时，B={xa＜x＜1}，
由A∩B≠，易知a＜1.
综上，a的取值范围是{aa＜1或a＞3}.
22.（14分）（2004年辽宁，18）设全集U=R.
（1）解关于x的不等式x－1+a－1＞0（a∈R）；
（2）记A为（1）中不等式的解集，集合B={xsin（πx－
）+cos（πx－）=0}，
若（UA）∩B恰有3个元素，求a的取值范围.
解：（1）由x－1+a－1＞0，得x－1＞1－a.
当a＞1时，解集是R；
当a≤1时，解集是{xx＜a或x＞2－a}.
（2）当a＞1时，UA=；
当a≤1时，UA={xa≤x≤2－a}.
因sin（πx－）+cos（πx－）=2［sin（πx－）cos+cos（πx－）sin］=2sinπx，
由sinπx=0，得πx=kπ（k∈Z），即x=k∈Z，所以B=Z.
当（UA）∩B恰有3个元素时，a应满足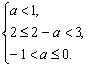
解得－1＜a≤0.