2006高考数学模拟卷(理)
(满分150分,考试时间120分钟)
第Ⅰ卷(选择题:共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中只有一项是符合题目要求的。
1、
下列各式:①2003![]() {xx≤2004};②2004∈{xx<2004};③{2004}
{xx≤2004};②2004∈{xx<2004};③{2004}![]() {xx≤2004};④ф∈{xx<2004}
( )
{xx≤2004};④ф∈{xx<2004}
( )
A、1个 B、2个 C、3个 D、4个
2、a=sin14°+cos14°, b=
sin16°+cos16°, c=![]() ,则a,b,c的大小关系是
( )
,则a,b,c的大小关系是
( )
A、a<b<c B、a<c<b C、b<c<a D、b<a<c
3、复数![]() 的模为
的模为![]() ,则实数a 的值是 ( )
,则实数a 的值是 ( )
A、![]() B、3 C、
B、3 C、![]() D、
D、![]()
4、不等式组![]() 表示的平面区域的面积为
( )
表示的平面区域的面积为
( )
A、12 B、16 C、24 D、28
5、已知ΔABC的三个顶点A、B、C及平面内一点P满足![]() ,则点P与ΔABC的关系为
( )
,则点P与ΔABC的关系为
( )
A、P在ΔABC的内部 B、P在ΔABC的外部
C、P在AB边所在的直线上 D、P在AC边所在的直线上
6、已知数列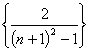 的前n项和为Sn,则
的前n项和为Sn,则![]() 等于
( )
等于
( )
A、0
B、1
C、![]() D、2
D、2
7、中心在原点,准线为x=±4,离心率为0.5的椭圆方程为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、下列四个命题中,正确命题的序号是 ( )
①“直线a、b是异面直线”的充分而不必要条件是“直线a、b不相交”;
②“直线l垂直于平面α内所有直线”的充要条件是“l ⊥平面α”;
③“直线a∥直线b” 的充要条件是“a平行于b所在的平面”;
④“直线a∥平面α”的必要而不充分条件是“直线a平行于α内的一条直线”。
A、①③ B、②④ C、①④ D、③④
9、有12 本不同的书,放在同一书架上,其中取3本要按固定顺序排列,全部放法的总数是 ( )
A、![]()
![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知函数是定义在R上的增函数,当x<0时,![]() ,那么
,那么![]() 的值是( )
的值是( )
A、-3 B、3 C、-2 D、2
11、已知![]() ,
,![]() ,则
,则![]() 的值为
( )
的值为
( )
A、-4 B、0 C、4 D、8
12、若以圆锥曲线的一条经过焦点的弦为直径的圆与对应的准线无公共点,则此圆锥曲线为( )
A、双曲线 B、椭圆 C、抛物线 D、椭圆或双曲线
第Ⅱ卷(非选择题:共90分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中的横线上。
13、二项式![]() 的展开式中。末两项的系数之和为7,且系数最大的一项的值为
的展开式中。末两项的系数之和为7,且系数最大的一项的值为![]() ,则x在[0,2π)内的值是___________________。
,则x在[0,2π)内的值是___________________。
14、已知两点M(-5,0),N(5,0),给出下列直线方程:
①5x-3y=0 ; ②5x-3y-52=0 ; ③x-y-4=0 ; ④4x-3y-15=0;在直线上存在点P满足MP=NP+6的所有直线方程是____________________。
15、已知![]() …
…![]() ,则
,则![]() __________________。
__________________。
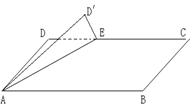 16、如图,矩形ABCD中,DC=
16、如图,矩形ABCD中,DC=![]() ,AD=1,在DC上截取DE=1,
,AD=1,在DC上截取DE=1,
将△ADE沿AE翻折到![]() 点,当点
点,当点![]() 在平面ABC上的射影落
在平面ABC上的射影落
在AE 上时,四棱锥![]() —ABCE的体积是_____________。
当点
—ABCE的体积是_____________。
当点![]() 在平面ABC上的射影落在AC上时,二面角
在平面ABC上的射影落在AC上时,二面角![]() 的余弦值是__________。
的余弦值是__________。
三、解答题:本大题共6小题,共74分。解答应写出必要的文字说明,证明过程及演算步骤。
17、(本题满分12分)已知关于x的方程![]() 的两根为
的两根为![]() ,
,![]() (0,2π);
(0,2π);
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求的m值;
(Ⅲ)求方程的两根及此时![]() 的值。
的值。
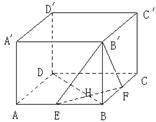 18、(本题满分12分)在棱长为a的正方体
18、(本题满分12分)在棱长为a的正方体![]() 中,,如图E、F分别为棱AB与BC的中点,EF∩BD=H;
中,,如图E、F分别为棱AB与BC的中点,EF∩BD=H;
(Ⅰ)求二面角![]() 的正切值;
的正切值;
(Ⅱ)试在棱![]() 上找一点M,使
上找一点M,使![]() ⊥面EFB¹,并证明你的结论;
⊥面EFB¹,并证明你的结论;
(Ⅲ)求点![]() 到面
到面![]() 的距离。
的距离。
19、(本题满分12分)某赛季足球联赛中,A队要和其他六个队的每一个队都要比赛一场,已知A队在六场比赛中任何一场比赛打胜、打败或打平的概率都是![]() ;
;
(Ⅰ)求A队在打完六场比赛后,胜的次数![]() 的分布列;
的分布列;
(Ⅱ)A队在打完六场比赛后,求胜的次数![]() 多于败的次数
多于败的次数![]() 的概率。
的概率。
20、(本题满分12分)已知函数![]() ,
,![]() ;
;
(Ⅰ)若![]() 在
在![]() 上是增函数,求a的取值范围;
上是增函数,求a的取值范围;
(Ⅱ)求![]() 在区间
在区间![]() 上的最大值。
上的最大值。
21、(本题满分12分)设![]() ,
,![]() 为直角坐标平面内x,y轴正方向上的单位向量,若向量
为直角坐标平面内x,y轴正方向上的单位向量,若向量![]() ,
,![]() ;且
;且![]() ;
;
(Ⅰ)过 点M(x,y)的轨迹C的方程;
(Ⅱ)过点(0,3)做直线l与曲线C交于A、B两点,设![]() ,是否存在这样的直线l ,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由。
,是否存在这样的直线l ,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由。
22、(本题满分14分)函数![]() 满足
满足![]() ,
,![]() ,且
,且![]() 时,
时,![]() ;
;
(Ⅰ)设![]() ,求数列
,求数列![]() 的通项;
的通项;
(Ⅱ)证明当![]() ,
,![]() 时,
时,![]() ;
;
(Ⅲ)判断![]() 的单调性,并证明。
的单调性,并证明。
高考数学模拟卷(理)答案
一、 选择题
1、A 2、B 3、C 4、C 5、D 6、C
7、B 8、C 9、A 10、D 11、D 12、B
二、 填空题
13、![]() ,
,![]() 14、②,③ 15、
14、②,③ 15、![]() 16、
16、![]() ,
,![]()
三、 解答题
17、解:(I)∵![]() 是方程
是方程![]() 的两根
的两根
∴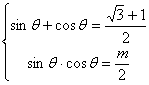
∴![]()
![]()
![]()
(II)由韦达定理得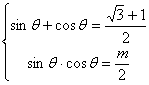 ∴
∴![]() ∴
∴![]()
(III)由(I)、(II)知原方程为![]() 解得
解得![]()
又由(II)知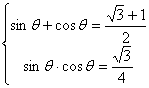 ,
,
∴![]() 或
或![]() 而
而![]()
∴![]() 的值为
的值为![]() 。
。
 18、解:(I)连结
18、解:(I)连结![]()
∵底面![]() 为正方形 ∴
为正方形 ∴![]()
又∵![]() 分别为
分别为![]() 的中点
的中点
∴![]() ∥
∥![]() , ∴
, ∴![]()
又∵棱![]() 底面
底面![]() ,
,![]() 底面
底面![]()
∴![]() 而
而![]() ∴
∴![]() 平面
平面![]() 又∵
又∵![]() 面
面![]() ,
,![]() 面
面![]() ∴
∴![]()
∴![]() 为二面角
为二面角![]() 的平面角
的平面角
在![]() 中
中![]() ∴
∴![]()
∴二面角![]() 的正切值的大小为
的正切值的大小为![]() 。
。
(II)在棱![]() 上取中点
上取中点![]() ,连结
,连结![]() ,则
,则![]() 面
面![]()
证明:连结![]() ∵
∵![]() 面
面![]() ,
,![]() 面
面![]() ∴
∴![]()
又∵![]() 面
面![]() ,∴
,∴![]() 为
为![]() 在面
在面![]() 内的射影。
内的射影。
在正方形![]() 中,
中,![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
故易得![]() ,于是由三垂线定理得
,于是由三垂线定理得![]() ,
,
而![]() 面
面![]() ,
,![]() 面
面![]() ,
,![]() ∴
∴![]() 面
面![]() 。
。
(III)设![]() 与面
与面![]() 交于
交于![]() ,则
,则![]() 为
为![]() 到面
到面![]() 的距离
的距离
∵![]() 面
面![]() ,
,![]() 面
面![]() ,
∴
,
∴![]()
在![]() 中,由射影定理
中,由射影定理![]()
而![]() ,
,
∴![]() 即
即![]() 到面
到面![]() 的距离为
的距离为![]() 。
。
19、解:(I)胜的次数![]() 的分布列
的分布列
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(II) 当![]() 时,
时,![]() ∴
∴![]() ;
;
当![]() 时,
时,![]() 或
或![]() ,
∴
,
∴![]()
同理
![]()
![]()
![]()
![]()
∴![]()
20、解:(I)由已知可得![]()
∵![]() 在
在![]() 上是增函数 ∴
上是增函数 ∴![]() 即
即![]()
而函数![]() 在
在![]() 上是增函数
∴
上是增函数
∴![]() ∴
∴![]()
又当![]() 时,
时,![]() 在
在![]() 也有
也有![]() ,满足
,满足![]() 在
在![]() 上是增函数
∴
上是增函数
∴![]() 即为所求。
即为所求。
(II)由(I)知![]() 在
在![]() 是增函数
是增函数
∴当![]() 时,
时,![]() ,
,
当![]() 时,令
时,令![]() 得
得![]()
∴当![]() 时,
时,![]() ;当
;当![]() 时
时![]()
∴当![]() 时,
时,![]()
故对![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 。
。
21、解:(I)∵![]() ,
,![]() ,且
,且![]()
∴点![]() 到两个定点
到两个定点![]() 的距离和为
的距离和为![]()
∴点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点的椭圆,其方程为
为焦点的椭圆,其方程为![]() 。
。
(II)∵![]() 过点
过点![]() ,若直线
,若直线![]() 的斜率不存在,则
的斜率不存在,则![]() 为椭圆的顶点
为椭圆的顶点
∵![]() ∴
∴![]() 与
与![]() 点重合,与四边形
点重合,与四边形![]() 是矩形矛盾
是矩形矛盾
故直线![]() 的斜率存在
的斜率存在
设![]() :
:![]() ,
,![]() ,
,![]()
由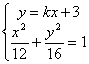 消去
消去![]() 得
得![]()
此时![]() 恒成立
恒成立
且![]() ,
,![]()
∵![]() ∴四边形
∴四边形![]() 是平行四边形
是平行四边形
若使得此平行四边形为矩形,则![]() 即
即![]()
又∵![]() ,
,![]() ∴
∴![]()
即![]()
即![]() 解得
解得![]() ∴
∴![]()
∴存在直线![]() ,方程为
,方程为![]() ,使得四边形
,使得四边形![]() 为矩形。
为矩形。
22、解:(I)∵![]() ∴
∴![]()
又![]() ∴
∴![]()
令![]() 则
则![]()
∴![]() 、
、![]()
故![]() 是以
是以![]() ,公差
,公差![]() 的等差数列
的等差数列
![]() 。
。
(II)证明: ①当![]() 时,
时,![]() 则
则![]() ∴
∴![]()
又![]() ∴
∴![]()
故当![]() 时命题成立
时命题成立
②假设当![]() 时命题成立,
时命题成立,
即当![]() 时
时![]()
则当![]() 时,
时,![]() ,
,![]()
则![]()
故当![]() 时命题成立
时命题成立
综上①②所述,当![]() 时
时![]() 。
。
(III)![]() 在
在![]() 上为单调递减
上为单调递减
证明:设![]() 且
且![]()
则![]()
当![]() 时,
时,![]() ∴
∴![]()
当![]() 时,由(II)知当
时,由(II)知当![]() 时,
时,![]() ,
,![]()
∴当![]() 时,
时,![]() 即
即![]()
∴![]()
∴当![]() 时,
时,![]()
故![]() 在
在![]() 上单调递减。
上单调递减。