高考数学中档题精选(4)
1.(本小题满分12分)
已知函数![]() 是常数),
是常数),
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若![]() 的最大值为1,求a的值.
的最大值为1,求a的值.
解:(Ⅰ)![]()
![]() ……2分
……2分
![]() ………………………………………4分
………………………………………4分
∴f(x)的最小正周期为2π …………………………………6分
(Ⅱ)![]() ………………………………8分
………………………………8分
∴f(x)的最大值为2+a…………………………………………………………10分
∴2+a=1 ∴a=-1………………………………………………………12分
2.(本小题满分12分)
数列{an} 的前n项和![]() ,其中a,b是常数.
,其中a,b是常数.
(Ⅰ)若{an}是等比数列,求a,b应满足的条件?
(Ⅱ)当{an}是等比数列时,求![]() 的值.
的值.
2.解:(理)(Ⅰ)由已知![]() ………………………………………………2分
………………………………………………2分
由![]() …………4分
…………4分
∴当a≠0时,{an} 从第二项起成等比数列.
若{an}是等比数列,则首项为a,公比为2.
∴2a+b=a ∴a+b=0……………………………………………………6分
∴若{an}为等比数列,a、b应满足的条件是a+b=0,且a、b均不为零.…8分
(Ⅱ)由(Ⅰ)![]() …………………………10分
…………………………10分
![]()
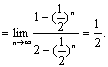 …………………12分
…………………12分
|
长方体ABCD—A1B1C1D1中,AB=BC=1,AA1=2,E
是侧棱BB1中点.
(Ⅰ)求证:直线AE⊥平面A1D1E;
(Ⅱ)求二面角E—AD1—A1的大小;
(Ⅲ)求三棱锥A—C1D1E的体积.
解:(Ⅰ)已知几何体为长方体
∴A1D1⊥平面ABB1A1
∴A1D1⊥AE………………………………2分
又AB=1,BB1=2,E为BB1的中点
∴△ABE为等腰直角三角形
 ∴AE=
∴AE=![]() 同理A1E=
同理A1E=![]()
∴∠AEA1为直角 即AE⊥A1E
∴AE⊥平面A1D1E………………………………4分
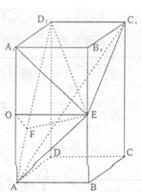
(Ⅱ)取AA1中点O,连OE,则EO⊥A1A、EO⊥A1D1、
∴EO⊥平面ADD1A1…………………………………………5分
过O在平面ADD1A1中作OF⊥AD1,交AD1于F 连结EF,则AD1⊥EF
∴∠EFO为二面角E—AD1—A1的平面角……………………7分
![]()
![]()
即二面角![]() ………………………………9分
………………………………9分
(Ⅲ)由于AB∥C1D1 ∴AB∥平面C1D1E
![]() …………………12分
…………………12分
高考数学中档题精选(5)
1.(12分)设a,b,c分别为△ABC的边BC,CA,AB的长,且![]() (m为常数).若
(m为常数).若![]() ,求m的值.
,求m的值.
解: 由![]()
![]() (6分)
(6分)
由正弦定理得![]() (8分)从而由余弦定理及
(8分)从而由余弦定理及![]() 得
得
![]() (12分)
(12分)
2.(12分)已知数列{an}的前n项的和为Sn,且![]() 且
且![]() .
.
(1)求证:![]() 为等差数列;
为等差数列;
(2)求:![]() 的值;
的值;
(3)求满足an>an-1的自然数n的集合.
解:(1)由![]() (2分)
(2分)
当n≥2时![]() 成等差数列
成等差数列 ![]() (3分)
(3分)
又∵当n=1时,![]() 而n=1时,
而n=1时,![]() (4分) 故当n≥1时,
(4分) 故当n≥1时,![]() 成等
成等
差数列
(5分)
(2)![]() (8分)
(8分)
(3)当n≥3时,![]() (9分)
(9分)
![]() ∴满足题设的n集合为{3、4、5、7}(12分)
∴满足题设的n集合为{3、4、5、7}(12分)
 3.(本小题满分12分).
3.(本小题满分12分).
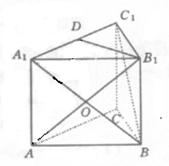
如图,正三棱柱ABC—A1B1C1的底面边长为2,侧棱长为![]() ,A1C1的中点为D.
,A1C1的中点为D.
(Ⅰ)求证BC1∥平面AB1D;
(Ⅱ)求二面角A1—B1D—A的大小;
(Ⅲ)求点B到平面的AB1D的距离.
解:(Ⅰ)连结A1B,设A1B与AB1相交于点O,则O为A1B的中点.
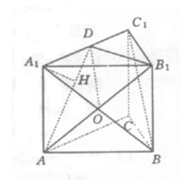 连结DO,因为D为A1C1中点,所以DO为△A1BC1的中位线,
连结DO,因为D为A1C1中点,所以DO为△A1BC1的中位线,
所以DO∥BC1.
又DO![]() 平面AB1D,BC1
平面AB1D,BC1![]() 平面AB1D
平面AB1D
所以BC1∥平面AB1D. ……4分
(Ⅱ)由题意知B1D是正△A1B1C1的中线,
所以A1C1⊥B1D.
在正三棱柱ABC—A1B1C1中,AA1⊥平面A1B1C1
所以AD⊥B1D,
所以∠ADA1是二面角A1—B1D—A的平面角……6分
在Rt△ADA1中,![]()
所以∠ADA1=60°,即二面角A1—B1D—A等于60°. ……8分
(Ⅱ)因为O为A1B中点,所以点B到平面AB1D的距离等于点A1到平面AB1D的距
离.由(Ⅱ)可知B1D⊥平面A1ACC1,
所以平面AB1D⊥平面A1ACC1,且平面AB1D∩平面A1ACC1=AD.
过点A1作A1H⊥AD,垂足为H,则A1H⊥平面AB1D.
所以线段A1H的长度就是点A1到平面AB1D的距离. ……11分
在Rt△A1AD中,![]()
所以点B到平面AB1D的距离等于![]() ……12分
……12分
或设点B到平面AB1D的距离为h,因为![]()
所以![]()
![]() ……12分
……12分
高考数学中档题精选(6)
1.已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 的最大值及最小值;
的最大值及最小值;
(3)写出函数![]() 的单调递增区间.
的单调递增区间.
解:(1)![]()
![]()
![]()
![]() 的最小正周期
的最小正周期![]() .
.
(2)当![]() 时,f(x)取得最大值2;
时,f(x)取得最大值2;
当![]() 时,f(x)取得最小值-2.
时,f(x)取得最小值-2.
(3)f(x)的单调递增区间为![]() .
.
2.有两个各项都是正数的数列{an},{bn},若对于任意自然数n都有an、bn2、 an+1成等差数列,bn2、an+1、bn+12成等比数列,
①求证:数列{bn}是等差数列;
②如果a1=1,b1=![]() ,记数列{
,记数列{![]() }的前n项和为Sn,求
}的前n项和为Sn,求![]() .
.
①证明:依题意:an+an+1=2bn2 bn2bn+12=an+12 又 an>0 ,bn>0
∴bn-1bn+bnbn+1=2bn2 ∴bn-1+bn+1=2bn 即{bn}是等差数列。
②解:由a1=1,b1=![]() 得a2=2×2-1=3, b2= ,∴bn= += ∴an=bnbn-1=
得a2=2×2-1=3, b2= ,∴bn= += ∴an=bnbn-1=
![]() .
.
3.在立方体ABCD—A1B1C1D1中,E,F,G,H分别是棱AB,
CC1,D1A1,BB1的中点.
(1)证明:FH∥平面A1EG;
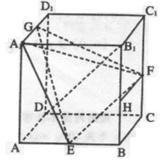 (2)若AB=a,求三棱锥A1—EFG的体积;
(2)若AB=a,求三棱锥A1—EFG的体积;
(3)证明B1D⊥平面EFG.
19.(理)(1)证明:∵FH∥B1C1,B1C1∥A1G,∴FH∥A1G.又A1G![]() 平面A1EG,FH
平面A1EG,FH![]() 平面A1EG,
平面A1EG,
∴FH∥平面A1EG.
(2)解:连结HA1,HE,HG,∵FH∥平面A1EG,∴![]() .
.
![]() (3)设BC的中点为M,连结EM,FM,AC,BD. ∴AC⊥BD,由三垂线定理,得AC⊥B1D,
(3)设BC的中点为M,连结EM,FM,AC,BD. ∴AC⊥BD,由三垂线定理,得AC⊥B1D,
又EM∥AC. ∴EM⊥B1D.同理FM⊥BD1,又EM与FM相交,∴B1D⊥平面EFM,B1D⊥EF.同理
B1D⊥FG,又EF与FG相交,∴B1D⊥平面EFG.
另证:∵EB1=ED,∴E在B1D的中垂面上,同理,F,G均在B1D的中垂面上,∴B1D⊥平面EFG