2004 届 高 三 数 学(理科)模 拟 试 题
命题人:城南中学 黄柏炯
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。
参考公式: 正棱锥、圆锥的侧面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
P(A·B)=P(A)·P(B) 母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率 其中R表示球的半径
![]()
第I卷(选择题,共60分)
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.函数 y=-x(x+2)(x≥0)的反函数定义域为 ( )
A. ![]() B.
B.![]() C. (0,1) D.
C. (0,1) D.![]()
2.若 的取值范围是 ( )
的取值范围是 ( )
A.[2,6] B.[2,5] C.[3,6] D.[3,5]
3.教室内有一直尺,无论怎样放置,在地面总有直线与直尺所在的直线 ( )
A.平行 B.垂直 C.相交 D.异面
4.函数![]() (
(![]() ,且
,且![]() )是偶函数,且在
)是偶函数,且在![]() 上单调递减,
上单调递减,
则![]() 与
与![]() 的大小关系是
( )
的大小关系是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.复平面内点Z1、Z2对应复数分别为z1 z2 若z1-z2=z1+z2(z1z2![]() 0)则向量
0)则向量![]() 所成
所成
的角为 ( )
A.0° B.60° C.90° D.120°
6.设曲线y=和曲线y=在它们交点处的两切线的夹角为θ,则tanθ=
( )
A.1 B. C. D.
7.设双曲线![]() 的右准线与两渐近线交于A、B两点,点F为右焦点,
的右准线与两渐近线交于A、B两点,点F为右焦点,
若以AB为直径的圆经过点F,则该双曲线的离心率为 ( )
A.![]() B.2 C.
B.2 C.![]() D.
D.![]()
8. 设函数![]() 的图象关于直线
的图象关于直线![]() 对称,它的周期是
对称,它的周期是![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9. 台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为 ( )
A.0.5小时 B.1小时 C.1.5小时 D.2小时
10.弹子跳棋共有60颗大小相同球形弹子,现在棋盘上将它叠成正四面体形球垛,使剩下的弹子尽可能的少,那么剩余的弹子共有 ( )
A.11颗 B.4颗 C.5颗 D.0颗
|
七种颜色分别涂在伞蓬的八个区域内,且恰有一种颜色涂在相对区域内,
则不同的颜色图案的此类太阳伞至多有 ( )
A. 40320种 B. 5040种
C. 20160种 D. 2520种
|
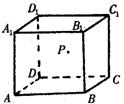
P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形
状为 ( )
 |
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13.二项式![]() 的展开式中,末尾两项的系数之和为7,且系数最大的一项的值
的展开式中,末尾两项的系数之和为7,且系数最大的一项的值
为![]() 则x在
则x在![]() 内的值为
.
内的值为
.
|
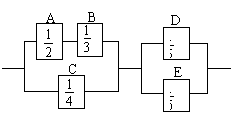
15. 如图:电路中五个方框均为保险匣。框
内数字为通电时保险丝被烧断的概率,
假定通电后保险丝是否烧断是相互独立
的,则通电后不断路的概率为 .
16. 同住一间寝室的四名女生,她们当中有一人在修指甲,一人在看书,一人在梳头发,另一人在听音乐。
①A不在修指甲,也不在看书 ②B不在听音乐,也不在修指甲
③如果A不在听音乐,那么C不在修指甲④D既不在看书,也不在修指甲
⑤C不在看书,也不在听音乐
若上面的命题都是真命题,问她们各在做什么?
A在 ; B在 ;
C在 ; D在 .
三、解答题(本大题共6小题,共74分解答应写出文字说明、证明过程或演算步骤)
.17. (本小题满分12分)若锐角![]()
(1)![]() ; (2)
; (2)![]()
| |
19. (本小题满分12分) 甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数![]() 的数学期望和方差.
的数学期望和方差.
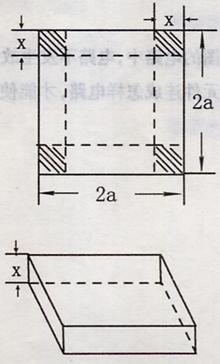
20、(本小题满分12分)从边长2a的正方形铁片的四个角各截一个边长为x的正方形,然后折成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正常数t .
|
(Ⅱ)x为何值时,容积V有最大值.
21.(本小题满分12分)已知点F(1,0),直线![]() ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M。 (1)求点M的轨迹C的方程;
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M。 (1)求点M的轨迹C的方程;
(2)设![]() 与x轴相交于H,直线BF与曲线C相交于P、Q两点,求证:向量
与x轴相交于H,直线BF与曲线C相交于P、Q两点,求证:向量![]() 与向量
与向量![]() 的夹角相等。
的夹角相等。
22.(本小题满分14分)已知![]() ,
,
(1)设![]() 的通项;
的通项;
(2)求![]() ;
;
(3)设![]() 是否存在整数m,对一切n∈N*,都有
是否存在整数m,对一切n∈N*,都有![]() 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由.
高 三 数 学(理科)模 拟 试 题 参 考 答 案
一.选择题:(本大题共12小题,每小题5分,共60分.)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | B | D | C | C | D | C | B | B | D | C |
二.填空题:本大题共4小题,每小题4分,共16分.
13.![]() 14、 84
15、
14、 84
15、 ![]()
16、 A在听音乐 ; B在看书; C在修指甲; D在梳头发
三.解答题:本大题共6小题,共74分.
17.(本小题满分12分)
解:(1)
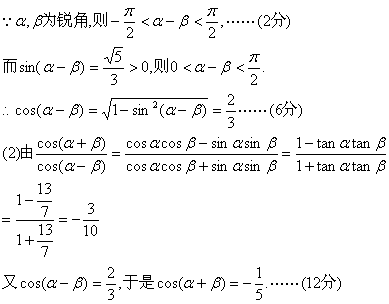
第(2)题另解:由![]() 得到
得到![]() ,再由(1)
,再由(1)![]()
得![]() , 解得
, 解得![]() ,
,
∴![]() ……(12分)
……(12分)
18.(本小题满分12分)
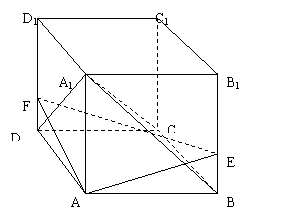
(1).证明:在正四棱柱中,A1D是A1C在平面ADD1A1上的射影,∵ A1D⊥AF,∴A1C⊥AF,同理由A1B⊥AE可得A1C⊥AE,∴A1C⊥平面AEF;……(4分)
(2).解:由AD=,AA=3,A1D⊥AF,A1B⊥AE,易求得BE=DF=1,连结BD、AC,设它们交于点O,取EF的中点M,连结AM、OM,∵AO⊥平面BEFD,OM⊥EF,∴∠AMO就是所求二面角的平面角…………(6分),在直角三角形AOM中,MO=1,![]() ,∴
,∴![]() ,∴
,∴![]() ;…………(8分)
;…………(8分)
(3).设B1到平面AEF的距离为h,在△AEF中,AM=![]() ,EF=
,EF=![]() ,由
,由![]() 得h=
得h=![]() …………(12分)
…………(12分)
19.(本小题满分12分)
解:(1)记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1,乙为P2. ……(2分)
则P(A)=P1=0.6,P(B)=P2
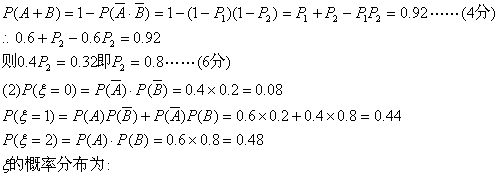
|
| 0 | 1 | 2 |
| P | 0.08 | 0.44 | 0.48 |
……………………………………(8分)
20.(本小题满分12分)
解:(Ⅰ)由已知正方形的长为2a-2x,高为x,
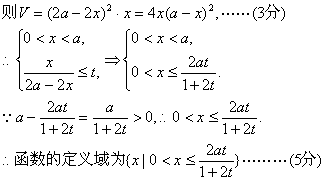
(Ⅱ)![]()
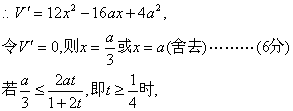
| x |
|
|
|
| V′ | + | 0 | - |

21.(本小题满分12分)
解(1)由已知易得MF=MB由抛物线定义得点M的轨迹方程为
![]() (
(![]() ≥0)……(4分)
≥0)……(4分)
(2)设直线![]() 方程
方程![]() 设P
设P![]()
则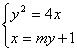 消去
消去![]() 得
得![]() ∴
∴![]()
而![]()
![]() ∴
∴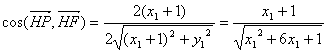
同理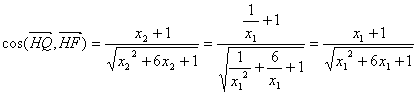
∵向量所成角范围在[0,![]() ]上
∴结论成立。……(12分)
]上
∴结论成立。……(12分)
22.(本小题满分14分)
解:(1)![]() 的值域y>0,解得
的值域y>0,解得![]()
![]() 知
知![]() 是等差数列(n∈N*).
是等差数列(n∈N*).
所以,![]() ……(4分)
……(4分)
(2)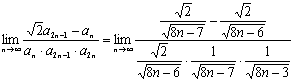
=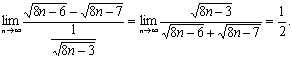 ……(8分)
……(8分)
(3)![]()
考虑![]()
所以,![]() 是递减数列,b1是最大的,
是递减数列,b1是最大的,![]() ……(12分)由于
……(12分)由于![]() 所以mmin=8…………(14分)
所以mmin=8…………(14分)
.