2006年 数 学 高 考 模 拟 卷　

裘桂红

正棱锥、圆锥的侧面积公式 其中c表示底面周长, l表示斜高或母 线长 球的体积公式 其中R表示球的半径

参考公式：

如果事件A、B互斥，那么　　　　　　　　　　　　　　

　 P（A+B）=P（A）+P（B）　　　　　　　　　　　　　　　

如果事件A、B相互独立，　　　　　　　　　　　　　　

P（A·B）=P（A）·（B）　　　　　　　　　　　　　

如果事件A在一次试验中发生的概率

　　　 是P，那么n次独立重复试验中恰好发　　　

生k次的概率

一、选择题（本大题共12个小题，每小题5分，共60分）

1.设P,Q是两个非空集合，PXQ={(a,b)aP,bQ},P={3,4,5},Q={4,5,6},

则PXQ中元素的个数是（ ）

A.3　　 B.4　　　C.7　　 D.12

2.角的始边为轴正半轴，顶点在原点，终边在射线4x+3y=0(x>0),则sin(sin+cot)+cos²的值为（）

A.8/5　 B.9/5　　 C.2/5　　D.1/5

3. 方程所对应的曲线图形是　　　　　　　　　　　　 （　　）

　　　　　

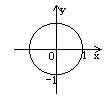
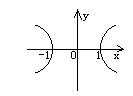
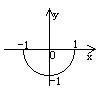
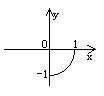
A.　　　　　  B.　　　　　　 C.　　　　　　　　  D.

4.等差数列｛a_n｝的前n项和为18,若S₃=1,a_n-2+a_n-1+a_n=3,则n的值为（）

A.9　　B.21　　 C.27　　 D.不确定

5．若是等差数列，且公差，则=　　　　　　　　　　 （　　）

　　　 A．－1　　　 B．1　　　C．　　　　　　　 D．不存在极限

6.如果a●b=a●c,且a为非零向量，那么（　）

A.b=c　　  B.b=c　　C.bc　  D.b,c在a方向上的投影相等

7.把函数y=x³的反函数的图象向右平移2个单位，再作以原点为中心的对称图形，则新图形的函数表达式是（　）

A.y=　　 B.y=-　　C.y=　  D.y=-

8.已知是直二面角，AB,设直线AB与所成的叫分别为，则

A.=　 B. ≥　 C. ≤　　D. <

9.设F₁,F₂是椭圆C的两个焦点，P是以F₁,F₂为直径的圆与椭圆C的交点，且PF₁F₂=5PF₂F₁,那么椭圆C的离心率为（　）

A./2　　 B. /2　　 C. /3　　D./3

10.欲购买价格为８元和１0的笔两种，用500元买8元一支的笔比买10一支的笔可多买30支以上，则10元一支的笔最多可买到（　）支

A.12　　B.13　　C.14　　D.15

11.已知曲线S:y=3x-x³及点P(2,2),则过P可向S引切线的条数为（）

A.0　 B.1　 C.2　　D.3

12.设O是正三棱锥P-ABC底面ABC的中心，过P的动平面与P-ABC的三条侧棱或其延长线的交点分别记为Q,R,S, 则和式

1/PQ+1/PR+1/PS(　)

A.有最大值而无最小值　B　 有小值而无最大值　

C.既有最大值又有最小值，且它们不相等

D.是一个与平面QRS位置无关的常量

二、填空题（本大题共4小题，每小题4分，共16分）

13．已知m、n表示直线，表示平面. 给出下列两个命题：

(1)； (2).

其中错误的一个命题是　　 （填命题序号）；因为当　　　　 时，该结论不成立.

14．设函数的定义域是　　　　　 ；的最大值是　　　　　　　 .

15.甲．乙．丙三人值日，从周一至周六，每人值班两天，若甲不值周一，乙不值周六，则可排出的值日表有　　 种.

16.1996年的诺贝尔化学奖授予对发现C₆₀有重大贡献的三位科学家.C₆₀是由60个碳原子组成的分子,它结构为简单多面体形状.这个多面体有6 0个顶点,每个顶点都引出3条棱,各面的形状为五边形或六边形,则C₆₀中五边形的面有　　个,六边形的面有　　  个.

三.解答题(本大题共六小题,共74分,解答应写出文字说明、证明过程或演算步骤)

17．（本小题满分12分）

　　　 已知A、B、C的坐标分别为A（3，0），B（0，3），C（），

　　　 （I）若求角的值；

　　　 （II）若的值.

18.(本小题12分)甲、乙两人独立解出某一道数学题的概率相同,已知该题被甲或乙解出的概率为0.36,求:

（I）　　　　　　　　　  甲独立解出该题的概率.

（II）　　　　　　　　 解出该题的人数的数学期望.

19．（本小题满分12分）

　　　 如图，正三棱柱ABC—A₁B₁C₁，BC=BB₁=1，D为BC上一点，

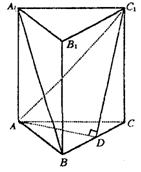
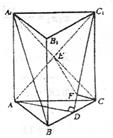
且满足AD⊥C₁D.

（I）求证：截面ADC₁⊥侧面BC₁；

（II）求二面角C—AC₁—D的正弦值；

（III）求直线A₁B与截面ADC₁距离.

20．（本小题满分2分）

　　　 设函数R），若使上为增函数，求a的取值范围

21．（本小题满分12分）

　　　 已知数列{}的前n项和为S_n，若问是否存在，使得对

于一切成立，请说明

22．（本小题满分14分）

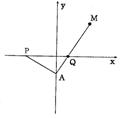
如图：P（－3，0），点A在y轴上，点Q在x轴的正半轴上，且

的延长线上取一点M，使=2.

（I）当A点在y轴上移动时，求动点M的轨迹C的方程；

（II）已知为

方向向量的直线l与轨迹C交于E、F两点，又点D（1，0），若∠EDF为钝角时，求k的取值范围.

参考答案及评分标准

一、选择题 （每小题5分，共60分

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	A	D	C	B	D	C	C	D	C	D	D

二、填空（每小题4分，共16分）

13．(2),n　 14.(0,+ ),-2　 15.42　 16.12,20

三、解答题

17．（本小题满分12分）

解：（1），…………2分

，

由得.　　 又.…………6分

（2）由

①………………7分

又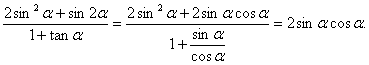………………9分

由①式两分平方得

……………………12分

18.（I）设甲、乙独立解出该题的概率为x，则该题不能被甲或乙解出的概率为(1-x)²,由题意可知，1-(1-x)²=0.36,解得x=0.2　　　　　 …………………………………… …………6分

　 (II)解出该题的人数的分布列为

	0	1	2
P	0.64	0.32	0.04

E=00.64+10.32+20.04=0.4…………………………………… …………12分

19．（I）由题知：ADCC₁， ADDC1，

知面ADC1面BC1

……………………………………………4分

I

（II）

故∠CEF为二面角C—AC₁—D的平面角…………………………………………6分

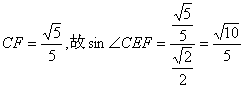在Rt△C₁CD中，求出………………8分

（III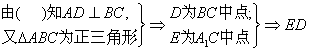）∥A₁B

∥面AC₁D，设B到面ADC₁距离为d……………………………………10分

…………………12分

注：其他证法相应给分

20．解……………………………………3分

由题知：上恒成立………………………6分

而……………………………………8分

令递增且最小值为…………………10分

……………………………………………………………………………12分

21．解：　 ①

　 ②

②－①得　 ③………………………………………………4分

若存在成立

则有

整理得…………………………………………………………8分

又由①式，得…………………………………………10分

因而存在满足题意………………………………………………12分

22．解：（I）设A（0，y₀）、Q（x₀，0）、M（x，y），

则

又 ①……3分

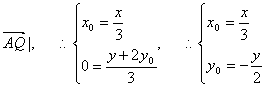　　　②

将②代入①，有…………………………………………6分

（II）联立，

得

　　③………………8分

又……10分

而

　　　④…………………………12分

将③代入④整理有

由题知………………………………14分