2006年佛山市高中毕业班高考调研会考
数学科试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分．考试用时120分钟．
注意事项：
1. 答卷前，考生务必将自己的姓名、考生号，用钢笔或签字笔填写在答题卡密封线内。
2. 选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案；不能答在试题卷上。
3. 非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡指定区域内的相应位置上；如需改动，先划掉原来的答案，然后在写上新的答案；不准采用铅笔和涂改液。不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁，考试结束后，将试卷和答题卡一并交回。
参考公式：
如果事件A、B互斥，那么 P（A+B）＝P（A）+P（B）
如果事件A、B相互独立，那么 P（A·B）＝P（A）·P（B） 如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
锥体的体积公式
其中S表示底面积，h表示高。
函数求导公式：
第Ⅰ卷（选择题，共50分）
一.选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的
（1）已知集合M={－1，0，1}，N={y︱y=cosx，x∈M}，则M∩N是
A．{－1，0，1} B．{0，1} C．{0} D．{1}
（2）函数y=cosx（sinx+cosx）的最小正周期为
A
B
C 
D
（3）下列各组命题中，“
或
”形式的复合命题为假命题的是
A．：函数
在
上是增函数；：函数
在上连续；
B．：导数为零的点一定是极值点；：最大值点的导数一定为零；
C．：互斥事件一定是对立事件；：对立事件一定是互斥事件；
D．：复数
与复数
对应点关于y轴对称；：复数
是纯虚数.
高三数学调研测试第1页（共4页）
|
|
x+4y≤1
A 3
B 4
C 5
D 
（5）盒中装有大小相同的黑、白两色小球，黑色小球15个，白色小球10个。现从中随机取出两个，若两个同色则甲获胜，若两个不同色则乙获胜。则甲、乙获胜的机会是
A甲多 B乙多 C一样多 D不确定的
（6）已知双曲线
上一点M到右焦点F的距离为11，N是MF之中点，O为坐标原点，则NO等于
A
B 
或
C D
（7）三棱柱ABC—A1B1C1中，P、Q分别为侧棱AA1、BB1上的点，且A1P=BQ，则四棱锥C1—APQB与三棱柱ABC—A1B1C1的体积之比是
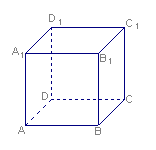
A B
C
D
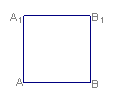
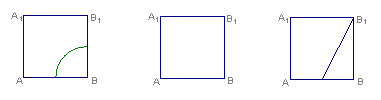（8）如图，正方体
中，在面
上一动点P，到
和BC的距离相等，则P点的轨迹是下图中的
A B C D
（9）已知f（x）,g（x）分别是定义在R上的奇函数和偶函数，当x<0时
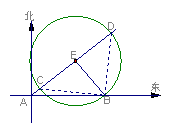
（10）台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为
A 0.5小时 B 1小时 C 1.5小时 D 2小时
第Ⅱ卷（非选择题，共100分）
二、填空题：本题共4小题，共20分.
（11）
则a= ,b=
.
（12）体操委员会由10位女性委员和5位男性委员组成，委员会要抽6位委员组团出国考
察，若以性别作分层，并在各层按比例抽样，则此考察团共有 种组成方式.（用数字作答）
高三数学调研测试第2页（共4页）
（13）将一张坐标纸折叠一次，使得点（0，0）与点（-1，1）重合，则这时与点（3，1）重合的点坐标为________.
（14） 定义运算a*b为：a*b=
，例如，1*2=1，则
的最大值是
.
三、解答题：本大题共6小题，共80分，解答应写出文字说明，证明过程或演算步骤．
（15）（本题满分12分）
已知数列{an}的前n项和为Sn，且满足
.
（Ⅰ）求证：{
}是等差数列；
（Ⅱ）求an的表达式.
（16）(本题满分13分)
已知函数
（Ⅰ）证明函数f(x)在
上为单调增函数；
（Ⅱ）证明方程f(x)=0没有负数根.
| |
，
．
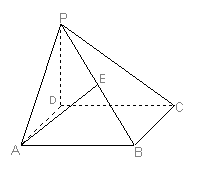
（Ⅰ）建立适当的空间坐标系，求出点E的坐标；
| |
（Ⅱ）在平面PAD内是否能够找到一点F， 使
| |
若不存在，则说明理由。
| |
（18）（本题满分13分）
高三（1）班的一个研究性学习小组在网上查知，某珍稀植物种子在一定条件下发芽成功的概率为
，该研究性学习小组又分成两个小组进行验证性实验，
（Ⅰ）第一小组做了5次这种植物种子的发芽实验（每次均种下一粒种子），求他们的实验至少有3次成功的概率；
（Ⅱ）第二小组做了若干次发芽实验（每次均种下一粒种子），如果在一次实验中种子发芽成功就停止实验，否则将继续进行下次实验，直到种子发芽成功为止，但发芽实验的次数最多不超过5次，求第二小组所做种子发芽实验的次数的概率分布列和期望。
高三数学调研测试第3页（共4页）
（19）（本题满分14分）
已知
=(x,0)，
=(1，y),
(Ⅰ)求点P(x，y)的轨迹C的方程；
(Ⅱ)若直线
：y=kx+m(km≠0)与曲线C交于A、B两点，点D(0，-1)在线段AB的垂直平分线上，试求实数m的取值范围。
（20）(本题满分15分)
由原点O向三次曲线
引切线，切于不同于点O的点
再由
引此曲线的切线，切于不同于的点
,如此继续地作下去，…，得到点列
试回答下列问题：
（Ⅰ）求
（Ⅱ）
的关系；
（Ⅲ）若a>0, 求证：当n为正偶数时，
| |
高三数学调研测试第4页（共4页
2005年佛山市高中毕业班高考调研测试
数学参考答案及平分意见
一．选择题（每小题5分）：DCBDC DBBDB
二．填空题（每小题4分）：
（11）
4 , -5 （12） 2100 . （13）(0,4). （14） 
.
解法提示：
（1）显然集合M、N只有公共元素1故选D.
（2）由
,知T=，选C.
（3） “
或”形式的复合命题为假，即、皆假，B中、 皆假，故选B.
（4）所求距离为点A（4,3）到直线3x+4y=12的距离，选D.
（5）甲获胜的概率为
易知
,故选C.
（6）设左焦点为
，连结
,则
∵a+c＝12＞11，∴点M不可能在双曲线左支上，由点M在双曲线右支上，结合定义可得
=21，故选D.
（7）利用
可得B.
（8）易知所求为面
上到点B的距离与到
的距离相等的点轨迹，依抛物线的定义知选B.
（9） 
由x<0时，
知奇函数
上为减函数，结合图象易知D正确.
（10）如图，
，
＝20（千米），
，选B.
（11）
由
（12） 易知考察团由4女2男组成，
=2100.
13.易得对称轴为直线y=x+1,设所求点为（m，n），由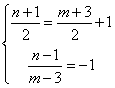
得
14. ∵
三、解答题
15．(本题满分12分)
(Ⅰ)证明：
2分
…………………………………………………………… 4分
又
是以2为首项，2为公差的等差数列……………………………6分
（Ⅱ）解：由（1）
…… …………………… 8分
当n≥2时，
（或n≥2时，
）
当n=1时，
………………………………………………………………10分
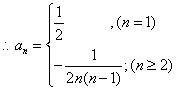……………………………………………………………………12分
（16）（本题满分13分）
解：（Ⅰ）
＝
……………………3分
又∵ a＞1， ∴ lna＞0．
∴ 当x＞－1时
， ∴f′(x)＞0 ………………5分
∴f(x)在上为单调递增函数。……………………………………………6分
（注：其它证法请参照给分）
（Ⅱ）假设存在x0＜0（x0≠－1）满足f(x0)＝0 …………………………7分
则
， 
……………8分
解得
，这与假设x0＜0矛盾。 …………………………………12分
∴上假设不成立，
即方程f(x)=0没有负数根。 ………………13分
（注：其它解法请参照给分）
（17）(本大题满分13分)
解：（Ⅰ）以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间直角坐标系，
如图示：则A（2，0，0），B（2，2，0），C（0，2，0），…1分
设P（0，0，2m）（m>0）,则E（1，1，m）， …2分
∴ 
（-1，1，m），
＝（0，0，2m）…3分
∴ 
，
，…5分
∴ 点E坐标是（1,1,1） ……………………………… 6分
（Ⅱ）∵ 
平面PAD， ∴ 可设F（x，0，z）
＝（x-1，-1，z-1），……7分
要使 EF⊥平面PCB ，则须
，且
………………………… 8分
即
，-1，
2，0，
=0, 且 ，-1，
0，2，-2）=0, …10分
解得
, 
…………………………………………………………………12分
∴ 存在点F（1，0，0），即点F是AD的中点时，EF⊥平面PCB。 ……………13分
（18）(本题满分13分)
解：（I）该事件为5次独立重复试验发生3次或4次或5次……………………1分
∴P=P5(3)+P5(4)+P5(5) ………………………………………………………………3分
=
…………………………………………………………6分
（II）
的可能取值分别为1，2，3，4，5. ……………………………………7分
分布列如下：
|
| 1 | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
|
……11分
∴ E=
……………………13分
（19）（本题满分14分）
解：（Ⅰ）
…………………………1分
∵
∴
…………………………………………………2分
∴
得
∴P点的轨迹方程为：
…………………………………………5分
（Ⅱ）由方程组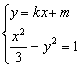
消去y，得(1-3k2)x2-6kmx-3m2-3=0(*)…………7分
依题意知1-3k2≠0, △=（-6km）2-4（
）(-3m2-3)=12（m2+1-3k2）>0 …8分
设x1,x2为方程（*）的两根，AB中点为（x0，y0）
则
…………………………………………………………………9分
故AB中点M的坐标为(
，
)…………………………………………10分
∴线段AB的垂直平分线方程为： 
……11分
将D(0，-1)坐标代入，化简得：4m=3k2-1…………………………………………12分
故m、k满足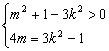
，消去k2得：m2-4m>0，m>4或m<0,……………13分
又∵4m=3k2-1>-1 ,∴m>-
,故m
……14分
（20）（本小题满分15分）
（Ⅰ）解：由
过曲线（1）上点
的切线
的方程是
y-
=
（
-
）,（
）………………2分
由它过原点，有
…… 4分
（Ⅱ）过曲线（1）上点
的切线
的方程是
………………6分
由
有
∵
…… 9分
（Ⅲ）由
得
……………………11分
故
……………12分
∴
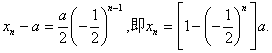………………………………13分
∵a>0,
∴当n为正偶数时，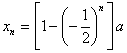
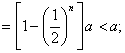……14分
当n为正奇数时，=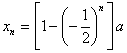
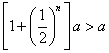。 …15分
（其它解法请参照给分）