2006年高考数学复习易做易错题选
函数、导数部分
一、选择题：
1、已知函数
，
，那么集合
中元素的个数为（ ）
A. 1 B. 0 C. 1或0 D. 1或2
2、已知函数
的定义域为[0，1]，值域为[1，2]，则函数
的定义域和值域分别是（ ）
A. [0，1] ，[1，2] B. [2，3] ，[3，4] C. [-2，-1] ，[1，2] D. [-1，2] ，[3，4]
3、已知0＜
＜1，
＜-1，则函数
的图象必定不经过（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
4、将函数
的图象向左平移一个单位得到图象
，再将向上平移一个单位得图象
，作出关于直线
对称的图象
，则对应的函数的解析式为（ ）
A. 
B.
C. 
D.
5、已知函数
在其定义域上单调递减，则函数
的单调减区间是（ ）
A. 
B. 
C.
D.
6、函数
在下面的哪个区间上是增函数（ ）
A. 
B.
C.
D. 
7、设
，
、
，且
＞
，则下列结论必成立的是（ ）
A. ＞
B. +＞0 C. ＜ D. 
＞
8、方程
和
的根分别是
、
，则有（ ）
A. ＜ B. ＞ C. = D. 无法确定与的大小
9、若、是关于
的方程
（
）的两个实根，则
的最大值等于（ ）
A. 6
B. 
C.
18
D. 19
10、若
与
在
上都是减函数，对函数
的单调性描述正确的是（ ）
A. 在
上是增函数
B. 在上是增函数
C. 在上是减函数
D. 在
上是增函数，在上是减函数
11、已知奇函数在上单调递减，且
，则不等式
＞0的解集是（ ）
A. 
B. 
C. 
D. 
12、不等式
≤
在
上恒成立，则实数的取值范围是（ ）
A. 
B.
C.
D.
13、方程
至少有一个负的实根的充要条件是（ ）
A. 0<≤1
B. ＜1 C.≤1 D. 0<≤1或< 0
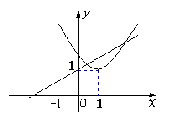
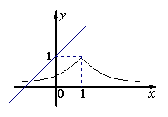14、在同一坐标系中，函数
与
（>0且≠1）的图象可能是
（A） （B）
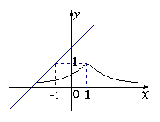
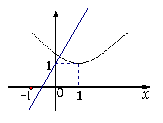
（C） （D）
15、函数是
上的奇函数，满足
，当∈（0，3）时
，则当∈（
，
）时， =（ ）
A. 
B.
C.
D.
16、函数
的图象关于原点中心对称，则
A. 在
上为增函数
B. 在上为减函数
C. 在
上为增函数，在
上为减函数
D. 在上为增函数，在上为减函数
17、
且
＜0，则
的取值范围是（ ）
A. 
B. 
C. 
D. 
18、二次函数满足
，又
，
，若在[0，
]上有最大值3，最小值1，则的取值范围是（ ）
A. B.
C.
D.
[2,4]
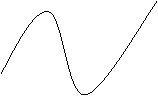
19、已知函数
的图象如图所示， 
则 （ ）
A. 
B.
C. 
D.
0 1
2
20、设
，
，
，则
的面积是 （ ）
A. 1
B. 
C.
4
D. 4
二、填空题：
21、函数
（＞-4）的值域是____________________.
22、函数
的值域是________________________.
23、函数
的值域是_________________________.
24、若实数满足
，则
=_____________________.
25、设定义在区间
上的函数
是奇函数，则实数的值是_______________________.
26、函数
（<-1）的反函数是_______________________.
27、函数
在（1，+
）上是增函数，则实数
的取值范围是____________________.
28、已知集合
，集合
，若
，则实数的取值范围是________________________.
29、已知函数是定义在R上的偶函数，当＜0时， 是单调递增的，则不等式
＞
的解集是_________________________.
30、已知
对任意
都有意义，则实数的取值范围是________________________________
31、函数
的定义域为
，值域为
，则实数的取值范围是______________________.
32、函数
的值域是______________________.
33、对于任意，函数表示
，
，
中的较大者，则
的最小值是____________________________.
34、已知＞1，＞＞0，若方程
的解是，则方程
的解是____________________.
35、已知函数
（≠0）在区间
上的最大值为1，则实数
的值是____________________.
36、对于任意实数、，定义运算*为：*=
，其中、、
为常数，等式右边的运算是通常的加法和乘法运算，现已知1*2=3，2*3=4，并且有一个非零常数，使得对于任意实数，都有*=，则=___________________________________.
37、已知函数
的定义域为，则实数的取值范围是________________________.
38、若函数
（>0且≠1）的值域为，则实数的取值范围是________________.
39、若曲线
与
有且只有一个公共点
，
为坐标原点，则
的取值范围是________________________.
40、若定义在区间
上的函数对上的任意
个值，，…，
，总满足
≤
，则称为上的凸函数.已知函数
在区间
上是“凸函数”，则在△
中，
的最大值是____________________.
答案：1 C 、 2 C 、3 A 、4 B 、5 D 、6 B 、7 D 、8 A 、9 C 、10 C 、11 B 、12 C 、13 C、14 C 、15 B 、 16 B 、17 A 、18 D 、19 A 、20 B 、
21 
、 22
、 23
、 24 10、 25 2、 26
27
、 28
、 29
、 30
、 31 
32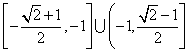
、 33 2、 34 
、35 
或
、 36
4、
37 
或
、 38 
或
、 39 
、40 
。