广西02-03年高考数学模拟试题
|
（第一卷）
一、选择题：（每小题5分，满分60分）
1、已知集合A={xx2+2ax+1=0}的真子集只有一个，则a值的集合是
A．（﹣1，1）； B．(﹣∞,﹣1)∪[1，+∞]；C．{﹣1，1}；D．{0}
2、若函数y=f(x)的反函数y=f－1(x)满足f－1(3)=0，则函数y=f(x+1)的图象必过点：
A．（0，3）； B．（－1，3）； C．（3，－1）； D．（1，3）
3、已知复数z1,z2分别满足 z1+i=2，z2－3－3i=3则 z1－z2的最大值为：
A．5； B．10； C．5+
； D．
4、数列
……的前n项和为：
A．
； B．
； C．
； D．
；
5、极坐标方程
sin
=sin2表示的曲线是：
A．圆； B．直线； C．两线直线 D．一条直线和一个圆。
6、已知一个复数的立方恰好等于它的共轭复数，则这样的复数共有：
A．3个； B．4个； C．5个； D．6个。
7、如图，在正方体ABCD—A1B1C1D1中，E、F是异面直
线AC，A1D的公垂线，则EF和ED1的关系是：
A． 异面； B．平行； C．垂直； D．相交。
8、设(2－X)5=a0+a1x+a2x+…+a5x5, 则a1+a3+a5的值为：
A．－120； B．－121； C．－122； D．－243。
9、要从一块斜边长为定值a的直角三角形纸片剪出一块圆形纸片，圆形纸片的最大面积为：
A．
a2； B．
； C．2πa2； D．
10、过点（1，4）的直线在x,y轴上的截距分别为a和b(a,b∈R+)，则a+b的最小值是：
A．9； B．8； C．7； D．6；
11、三人互相传球，由甲开始发球并作为第一次传球。经过5次传球后，球仍回到甲手中，则不同的传球方式共有：
A．6种； B．8种； C．10种； D．16种。
12、定义在R上的偶函数f(x)满足f(x+2)=f(x－2)，若f(x)在[﹣2，0]上递增，则
A．f(1)>f(5.5) ; B．f(1)<f(5.5)
C．f(1)=f(5.5) D．以上都不对。
（第二卷）
二、填空题：（每小题4分，满分16分）
13、（理）：arg(－1+3i)=___________________________________
（文）：arg(－1+
i)=_________________________________
14、等边圆柱的内切球和以此等边圆柱的下底面为底面，上底面圆心为顶点的圆锥的体积之比为：_____________________________________
15、（1－tg46°）(1－tg89°)的值为_______________________
16、对双曲线C1和C2有以下四个命题：（1）有相同的渐近线；（2）有相同的渐近线和离心率；（3）有相同的渐近线且四个焦点共圆；（4）四个焦点共圆且离心率相等；则能使C1和C2是共轭双曲线的命题的序号是________________________
三、解答题：
17、复数z1=cos2a+i2sina, a∈R, 且 z1=
，
（1） 求复数z1，及其辐角主值arg z1；
（2）
若复数z满足：z－z1+z－
=2，在复平面内将z对应的点集绕原点逆时针旋转，求旋转过程中该点集所扫过的图形的面积；（满分12分）
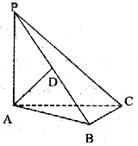18、如图三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=90°，2BC=AC，D为PB中点。
（1） 求异面直线AD与PC所成角的大小；
（2） 求二面角A-PC-B的正弦值。（满分12分）
19、已知等差数列{an}的首项为1，公差为d，前n项和为An；等比数列{bn}的首项为1，公比为q，（q<1）,前n项和为Bn，设Sn=B1+B2+…+Bn,
（1） 用n和q表示Sn；
（2）
|
=1，求数列{an},{bn}的通项公式；（满分12分）
20、某市要给面积为2640万亩的一片荒地绿化造林，若从2003年初开始绿化造林，第一年造林150万亩，以后每年比前一年多绿化75万亩，但每年的成活率仅为80%。
（1） 问：到哪一年底可将这片荒地全都绿化？
（2） 若每万亩绿化造林所植成活树苗的木材量为0.1万立方米，每年树木木材量的自然生长率为20%，那么当这片荒地全部绿化完的那一年底，一共有木材多少万立方米？（保留1位小数，1.29=5.16, 1.28=4.30）（满分12分）
21、已知直线
x+1=0，动圆P与直线相切并与定圆(x－2)2+y2=4相外切。
（1） 求动圆圆心P的轨迹C的方程；
（2）
若过原点的直线与曲线C交于A，B两点，问：是否存在以AB为直径的圆与直线相切？若存在，求出直线AB的方程；若不存在，说明理由。（满分12分）
22、已知二次函数f(x)=ax2+bx+c(a>0, b≠0)
（1） 若f(0)=f(1)=f(﹣1)=1，求f(x)的解析式；
（2）
若b≤a, f(0)≤1,f(1)≤1,f(﹣1)≤1。求证：当x≤1时，f(x)≤
。（满分14分）