2008年普通高等学校招生全国统一考试
数学分类解析—概率统计
一．选择题：
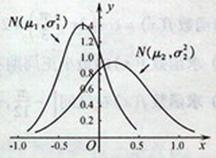
1. 
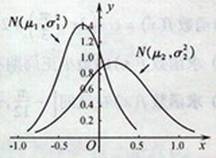(安徽理)（10）．设两个正态分布
和
的密度函数图像如图所示。则有（ A ）
A． 
B．
C．
D．
2.（福建理）(5)某一批花生种子，如果每1粒发牙的概率为
,那么播下4粒种子恰有2粒发芽的概率是 （B）
A.
B.
C. 
D.
3. （福建文）(5)某一批花生种子，如果每1粒发芽的概率为，那么播下3粒种子恰有2粒发芽的概率是 （C）
A.
B.
C.
D.
| 一年级 | 二年级 | 三年级 | |
| 女生 | 373 |
|
|
| 男生 | 377 | 370 |
|
4. （广东理）（3）．某校共有学生2000名，各年级男、女生人数如表1．已知在全校 学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为（ C ）
A．24 B．18 C．16 D．12
5.（湖南理） 4.设随机变量
服从正态分布N(2,9) ,若P (＞c+1)=P(＜c－
,则c=(B)
A.1 B.2 C.3 D.4
6. （江西文）（11）．电子钟一天显示的时间是从00:00到23:59，每一时刻都由四个数字组成，则一天中任一时刻显示的四个数字之和为23的概率为 （C）
A．
B．
C．
D．
7. （辽宁理文）（7）.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( C )
A.
B.
C.
D.
8.（山东理）（7）在某地的奥运火炬传递活动中，有编号为1，2，3，…，18的18名火炬手.若从中任选3人，则选出的火炬手的编号能组成3为公差的等差数列的概率为（B）
（A）
（B）
（C）
（D）
9.（山东理）
(8)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字，右边的数字表示城镇居民百户家庭人口数的个位数字，从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为（b）
（A）304.6 （B）303.6 (C)302.6 (D)301.6
10.（山东文）9．从某项综合能力测试中抽取100人的成绩，统计如表，则这100人成绩的标准差为（ B ）
| 分数 | 5 | 4 | 3 | 2 | 1 |
| 人数 | 20 | 10 | 30 | 30 | 10 |
A．
B．
C．3 D．
10.（陕西文）（3）．某林场有树苗30000棵，其中松树苗4000棵．为调查树苗的生长情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中松树苗的数量为（ C ）
A．30 B．25 C．20 D．15
11.（重庆理）(5)已知随机变量服从正态分布N(3,a2),则P(
＝（D）
(A)
(B)
(C) (D)
12. （重庆文）(5)某交高三年级有男生500人，女生400人，为了解该年级学生的健康情况，从男生中任意抽取25人，从女生中任意抽取20人进行调查.这种抽样方法是（D）
(A)简单随机抽样法 (B)抽签法
(C)随机数表法 (D)分层抽样法
13．（重庆文）(9)从编号为1,2,…,10的10个大小相同的球中任取4个，则所取4个球的最大号码是6的概率为 （B）
(A)
(B)
(C)
(D)
二．填空题：
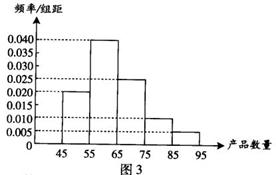1.（广东文） （11）.为了调查某厂工人生产某种产品的能力，随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为
，
，
由此得到频率分布直方图如图，则这20名工人中一天生产该产品数量在
的人数是 13 .
2.（海南宁夏理文）（16）．从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度（单位：mm），结果如下：
甲品种：271 273 280 285 285 287 292 294 295 301 303 303 307
308 310 314 319 323 325 325 328 331 334 337 352
乙品种：284 292 295 304 306 307 312 313 315 315 316 318 318
320 322 322 324 327 329 331 333 336 337 343 356
由以上数据设计了如下茎叶图
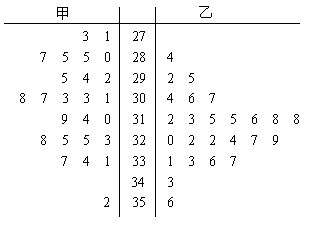
根据以上茎叶图，对甲、乙两品种棉花的纤维长度作比较，写出两个统计结论：
① ；
② ．
以下任填两个：（1）．乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度（或：乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度）．
（2）．甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散．（或：乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中（稳定）．甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大）．
（3）．甲品种棉花的纤维长度的中位数为307mm，乙品种棉花的纤维长度的中位数为318mm．
（4）．乙品种棉花的纤维长度基本上是对称的，而且大多集中在中间（均值附近）．甲品种棉花的纤维长度除一个特殊值（352）外，也大致对称，其分布较均匀．
3. （湖北文）11.一个公司共有1 000名员工，下设一些部门，要采用分层抽样方法从全体员工中抽取一个容量为50的样本，已知某部门有200名员工，那么从该部门抽取的工人数是 10 .
4．（湖北文）14.明天上午李明要参加奥运志愿者活动，为了准时起床，他用甲、乙两个闹钟叫醒自己，假设甲闹钟准时响的概率是0.80，乙闹钟准时响的概率是0.90，则两个闹钟至少有一准时响的概率是 0.98 .
5. （湖南理）15.对有n(n≥4)个元素的总体｛1,2,3,…,n｝进行抽样，先将总体分成两个子总体｛1,2,…，m｝和｛m+1、m+2,…，n｝(m是给定的正整数，且2≤m≤n-2),再从每个子总体中各随机抽取2个元素组成样本，用Pij表示元素i和f同时出现在样本中的概率，则P1m=
;所有Pif(1≤i＜j≤
的和等于 6 .
6. （湖南文）（12）从某地区15000位老人中随机抽取500人，其生活能否自理的情况如下表所示：
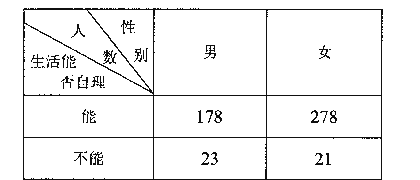
则该地区生活不能自理的老人中男性比女性约多____60____人。
7.（江苏）（2）．一个骰子连续投2次，点数和为4的概率
8.（江苏）（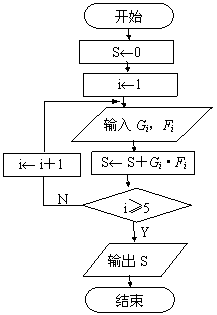
7）．某地区为了解70~80岁老人的日平均睡眠时间（单位：h），现随机地选择50位老人做调查，下表是50位老人日睡眠时间频率分布表：
| 序号 （i） | 分组 睡眠时间 | 组中值 （Gi） | 频数 （人数） | 频率 （Fi） |
| 1 | [4，5） | 4.5 | 6 | 0.12 |
| 2 | [5，6） | 5.5 | 10 | 0.20 |
| 3 | [6，7） | 6.5 | 20 | 0.40 |
| 4 | [7，8） | 7.5 | 10 | 0.20 |
| 5 | [8，9] | 8.5 | 4 | 0.08 |
在上述统计数据的分析中，一部分计算见算法流程图，则输出的S的值为 6.42 ．
9.（上海理文）（7）.在平面直角坐标系中，从六个点：A(0,0)、B(2,0)、C(1,1)、D(0,2)、E(2,2)、F(3,3)中任取三个，这三点能构成三角形的概率是（结果用分数表示）
10.（上海理文）（9）.已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12，13.7，18.3，20，且总体的中位数为10.5，若要使该总体的方差最小，则a、b的取值分别是
10.5和10.5
11.（上海文）8．在平面直角坐标系中，从五个点： 
中任取三个，这三点能构成三角形的概率是（结果用分数表示）．
12. （天津文）（11）．一个单位共有职工200人，其中不超过45岁的有120人，超过45岁的有80人．为了调查职工的健康状况，用分层抽样的方法从全体职工中抽取一个容量为25的样本，应抽取超过45岁的职工 10 人．
13.
三．解答题：
1.（安徽理）(19)．（本小题满分12分）
为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物。某人一次种植了n株沙柳，各株沙柳成活与否是相互独立的，成活率为p，设
为成活沙柳的株数，数学期望
，标准差
为
。
（1）求n,p的值并写出的分布列；
（2）若有3株或3株以上的沙柳未成活，则需要补种，求需要补种沙柳的概率
解：(1)由
得
,从而
的分布列为
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
|
(2)记”需要补种沙柳”为事件A, 则
得
或 
2．（安徽文）（18）．（本小题满分12分）
在某次普通话测试中，为测试汉字发音水平，设置了10张卡片，每张卡片印有一个汉字的拼音，其中恰有3张卡片上的拼音带有后鼻音“g”.
（1）现对三位被测试者先后进行测试，第一位被测试者从这10张卡片总随机抽取1张，测试后放回，余下2位的测试，也按同样的方法进行。求这三位被测试者抽取的卡片上，拼音都带有后鼻音“g”的概率。
（2）若某位被测试者从10张卡片中一次随机抽取3张，求这三张卡片上，拼音带有后鼻音“g”的卡片不少于2张的概率。
解：（1）每次测试中，被测试者从10张卡片中随机抽取1张卡片上，拼音带有后鼻音“g”的概率为
，因为三位被测试者分别随机抽取一张卡片的事件是相互独立的，因而所求的概率为
。
（2）设
表示所抽取的三张卡片中，恰有
张卡片带有后鼻音“g”的事件，且其相应的概率为
则
, 
因而所求概率为 
。
3．（北京理（17），文（18））（本小题共13分）甲、乙等五名奥运志愿者被随机地分到
四个不同的岗位服务，每个岗位至少有一名志愿者．
（1）求甲、乙两人同时参加
岗位服务的概率；
（2）求甲、乙两人不在同一个岗位服务的概率；
（3）设随机变量为这五名志愿者中参加岗位服务的人数，求的分布列．
解：（1）记甲、乙两人同时参加岗位服务为事件
，那么
，
即甲、乙两人同时参加岗位服务的概率是
．
（2）记甲、乙两人同时参加同一岗位服务为事件
，那么
，
所以，甲、乙两人不在同一岗位服务的概率是
．
（3）随机变量可能取的值为1，2．事件“
”是指有两人同时参加岗位服务，
则
．所以
，的分布列是
|
| 1 | 3 |
|
|
|
|
4．（福建理）（20）（本小题满分12分）
某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可继续参加科 目B的考试.已知每个科目只允许有一次补考机会，两个科目成绩均合格方可获得证 书.现某人参加这项考试，科目A每次考试成绩合格的概率均为，科目B每次考试 成绩合格的概率均为.假设各次考试成绩合格与否均互不影响.
（1）求他不需要补考就可获得证书的概率；
（2）在这项考试过程中，假设他不放弃所有的考试机会，记他参加考试的次数为
，求的数学期望E.
解:设“科目A第一次考试合格”为事件A，“科目A补考合格”为事件A2；“科目B第一次考试合格”为事件B，“科目B补考合格”为事件B.
(1)不需要补考就获得证书的事件为A1·B1,注意到A1与B1相互独立，
则
.
答：该考生不需要补考就获得证书的概率为.
(2)由已知得，＝2，3，4，注意到各事件之间的独立性与互斥性，可得
故
答：该考生参加考试次数的数学期望为
.
5．（福建文）（18）（本小题满分12分）三人独立破译同一份密码.已知三人各自破译出密码的概率分别为
且他们是否破译出密码互不影响.
(1)求恰有二人破译出密码的概率；
(2)“密码被破译”与“密码未被破译”的概率哪个大？说明理由.
解：记“第i个人破译出密码”为事件A1(i=1,2,3)，依题意有
且A1，A2，A3相互独立.
（1）设“恰好二人破译出密码”为事件B，则有
B＝A1·A2·
·A1·
·A3+
·A2·A3且A1·A2·，A1··A3，·A2·A3
彼此互斥
于是P(B)=P(A1·A2·)+P（A1··A3）+P（·A2·A3）
＝
＝
.
答：恰好二人破译出密码的概率为.
（2）设“密码被破译”为事件C，“密码未被破译”为事件D.
D＝··，且，，互相独立，则有
P（D）＝P（）·P（）·P（）＝
＝.
而P（C）＝1-P（D）＝，故P（C）＞P（D）.
答：密码被破译的概率比密码未被破译的概率大.
6．（广东理）（17）．（本小题满分13分）随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润（单位：万元）为．
（1）求的分布列；（2）求1件产品的平均利润（即的数学期望）；
（3）经技术革新后，仍有四个等级的产品，但次品率降为
，一等品率提高为
．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？
解：的所有可能取值有6，2，1，-2；
，
，
|
| 6 | 2 | 1 |
|
|
| 0.63 | 0.25 | 0.1 | 0.02 |
故的分布列为：
（2）
（3）设技术革新后的三等品率为
，则此时1件产品的平均利润为
依题意，
，即
，解得
所以三等品率最多为
7．（广东文）（19）.（本小题满分13分）某初级中学共有学生2000名，各年级男、女生人数如下表：
| 初一年级 | 初二年级 | 初三年级 | |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.
（1） 求x的值；
（2） 现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？
（3）
已知y
245,z245,求初三年级中女生比男生多的概率.
解：（1）
（2）初三年级人数为y＋z＝2000－（373＋377＋380＋370）＝500，
现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为：
名
（3）设初三年级女生比男生多的事件为A ，初三年级女生男生数记为（y，z）；
由（2）知 
，且 
,基本事件空间包含的基本事件有：
（245，255）、（246，254）、（247，253）、……（255，245）共11个
事件A包含的基本事件有：（251，249）、（252，248）、（253，247）、(254,246)、(255,245) 共5个 
8．（海南宁夏理）（19）．（本小题满分12分）
两个投资项目的利润率分别为随机变量X1和X2．根据市场分析，X1和X2的分布列分别为
| X1 | 5％ | 10％ |
P | 0.8 | 0.2 |
| X2 | 2％ | 8％ | 12％ |
P | 0.2 | 0.5 | 0.3 |
（1）在两个项目上各投资100万元，Y1和Y2分别表示投资项目A和B所获得的利润，求方差DY1，DY2；
（2）将
万元投资A项目，
万元投资B项目，
表示投资A项目所得利润的方差与投资B项目所得利润的方差的和．求的最小值，并指出x为何值时，取到最小值．（注：
）
解：（1）由题设可知
和
的分布列分别为
| Y1 | 5 | 10 |
P | 0.8 | 0.2 |
| Y2 | 2 | 8 | 12 |
P | 0.2 | 0.5 | 0.3 |
，
，
，
．
（2）
，
当
时，
为最小值．
9．（海南宁夏文）（19）．（本小题满分12分）为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查．6人得分情况如下：
5，6，7，8，9，10．
把这6名学生的得分看成一个总体．
（1）求该总体的平均数；
（2）用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本．求该样本平均数与总体平均数之差的绝对值不超过0.5的概率．
解：（1）总体平均数为
．
（2）设表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”．
从总体中抽取2个个体全部可能的基本结果有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
．
共15个基本结果．
事件包括的基本结果有：，，，，，，．
共有7个基本结果．
所以所求的概率为 
．
10．（湖北理）（17）（本小题满分12分）
袋中有20个大小相同的球，其中记上0号的有10个，记上n号的有n个（n=1,2,3,4）.现从袋中任取一球.ξ表示所取球的标号.
（1）求ξ的分布列，期望和方差；
（2）若η=aξ-b,Eη=1,Dη=11,试求a,b的值.
解：（1）的分布列为：
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
∴
（2）由
，得a2×2.75＝11，即
又
所以
当a=2时，由1＝2×1.5+b,得b=-2;
当a=-2时，由1＝-2×1.5+b，得b=4.
∴
或
即为所求.
11．（湖南理）（16）（本小题满分12分）甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约.乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约.设每人面试合格的概率都是，且面试是否合格互不影响.求：
（1）至少有1人面试合格的概率;
（2）签约人数
的分布列和数学期望.
解 用A，B，C分别表示事件甲、乙、丙面试合格.由题意知A，B，C相互独立，且
P（A）＝P（B）＝P（C）＝.
（1）至少有1人面试合格的概率是
（2）的可能取值为0，1，2，3.
＝
＝
=
=
所以，
的分布列是
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
的期望
12．（湖南文）（16）．（本小题满分12分）甲乙丙三人参加一家公司的招聘面试，面试合格者可正式签约。甲表示只要面试合格
就签约，乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约。设每人面试合格的概率都是
，且面试是否合格互不影响。求：
（1）至少一人面试合格的概率；
（2）没有人签约的概率。
解：用A,B,C分别表示事件甲、乙、丙面试合格．由题意知A,B,C相互独立，
且
（1）至少有一人面试合格的概率是
（2）没有人签约的概率为
13．（江西理）18．（本小题满分12分）因冰雪灾害，某柑桔基地果林严重受损，为此有关专家提出两种拯救果树的方案，每种方案都需分两年实施．若实施方案一，预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4；第二年可以使柑桔产量为第一年产量的1.25倍、1.0倍的概率分别是0.5、0.5．若实施方案二，预计第一年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5；第二年可以使柑桔产量为第一年产量的1.2倍、1.0倍的概率分别是0.4、0.6．实施每种方案第一年与第二年相互独立，令
表示方案实施两年后柑桔产量达到灾前产量的倍数．
（1）写出ξ1、ξ2的分布列；
（2）实施哪种方案，两年后柑桔产量超过灾前产量的概率更大?
（3）不管哪种方案，如果实施两年后柑桔产量达不到、恰好达到、超过灾前产量，预计利润分别为10万元、15万元、20万元．问实施哪种方案的平均利润更大?
解：（1）ξ1的分布列为
| ξ1 | 0.8 | 0.9 | 1 | 1.125 | 1.25 |
| P1 | 0.2 | 0.15 | 0.35 | 0.15 | 0.15 |
ξ2的分布列为
| ξ2 | 0.8 | 0.96 | 1 | 1.2 | 1.44 |
| P2 | 0.3 | 0.2 | 0.18 | 0.24 | 0.08 |
（2）由（1）可得P1＞1的概率P（P1＞1）= 0.15 + 0.15 = 0.3，
P2＞1的概率P（P2＞1）= 0.24 + 0.08 = 0.32，
可见，P（P2＞1）＞P（P1＞1）
∴实施方案2，两年后产量超过灾前概率更大。
（3）设实施方案1、2的平均利润分别为利润1、利润2，根据题意
利润1 = （0.2 +0.15）×10 + 0.35×15 + （0.15 + 0.15）×20
= 14.75（万元）
利润2 = （0.3 + 0.2）×10 + 0.18×15 + （0.24 + 0.08）×20
= 14.1（万元）
∴利润1＞利润2，
∴实施方案1平均利润更大。
14．（江西文）（18）．因冰雪灾害，某柑桔基地果林严重受损，为此有关专家提出一种拯救果树的方案，该方案需分两年实施且相互独立．该方案预计第一年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.2、0.4、0.4；第二年可以使柑桔产量为第一年产量的1.5倍、1.25倍、1.0倍的概率分别是0.3、0.3、0.4．
（1）求两年后柑桔产量恰好达到灾前产量的概率；
（2）求两年后柑桔产量超过灾前产量的概率.
解：（1）令A表示两年后柑桔产量恰好达到灾前产量这一事件
（2）令B表示两年后柑桔产量超过灾前产量这一事件
15．（辽宁理）（18）.某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
| 周销售量 | 2 | 3 | 4 |
| 频数 | 20 | 50 | 30 |
⑴根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵已知每吨该商品的销售利润为2千元,表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求的分布列和数学期望.
解：（1）周销售量为2吨，3吨和4吨的频率分别为0.2,0.5和0.3.
（2）的可能值为8，10，12，14，16，且
P（=8）=0.22=0.04,
P（=10）=2×0.2×0.5=0.2,
P（=12）=0.52+2×0.2×0.3=0.37,
P（=14）=2×0.5×0.3=0.3,
P（=16）=0.32=0.09.
的分布列为
|
| 8 | 10 | 12 | 14 | 16 |
P | 0.04 | 0.2 | 0.37 | 0.3 | 0.09 |
F=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4（千元）
16．（辽宁文）（18）．（本小题满分12分）
某批发市场对某种商品的周销售量（单位：吨）进行统计，最近100周的统计结果如下表所示：
| 周销售量 | 2 | 3 | 4 |
| 频数 | 20 | 50 | 30 |
（1）根据上面统计结果，求周销售量分别为2吨，3吨和4吨的频率；
（2）若以上述频率作为概率，且各周的销售量相互独立，求
（ⅰ）4周中该种商品至少有一周的销售量为4吨的概率；
（ⅱ）该种商品4周的销售量总和至少为15吨的概率．
解：（1）周销售量为2吨，3吨和4吨的频率分别为0.2，0.5和0.3．
（2）由题意知一周的销售量为2吨，3吨和4吨的频率分别为0.2，0.5和0.3，故所求的概率为
（ⅰ）
．
（ⅱ）
．
19．（全国Ⅰ理；文只做（1））20．（本小题满分12分）已知5只动物中有1只患有某种疾病，需要通过化验血液来确定患病的动物．血液化验结果呈阳性的即为患病动物，呈阴性即没患病．下面是两种化验方法：
方案甲：逐个化验，直到能确定患病动物为止．
方案乙：先任取3只，将它们的血液混在一起化验．若结果呈阳性则表明患病动物为这3只中的1只，然后再逐个化验，直到能确定患病动物为止；若结果呈阴性则在另外2只中任取1只化验．
（1）求依方案甲所需化验次数不少于依方案乙所需化验次数的概率；
（2）表示依方案乙所需化验次数，求的期望．
解：（1）对于甲：
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 概率 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
对于乙：
| 次数 | 2 | 3 | 4 |
| 概率 | 0.4 | 0.4 | 0.2 |
．
（2）表示依方案乙所需化验次数，的期望为
20．（全国Ⅱ理）（18）．（本小题满分12分）购买某种保险，每个投保人每年度向保险公司交纳保费
元，若投保人在购买保险的一年度内出险，则可以获得10 000元的赔偿金．假定在一年度内有10
000人购买了这种保险，且各投保人是否出险相互独立．已知保险公司在一年度内至少支付赔偿金10 000元的概率为
．
（1）求一投保人在一年度内出险的概率
；
（2）设保险公司开办该项险种业务除赔偿金外的成本为50 000元，为保证盈利的期望不小于0，求每位投保人应交纳的最低保费（单位：元）．
解：各投保人是否出险互相独立，且出险的概率都是，记投保的10 000人中出险的人数为，则
．
（1）记表示事件：保险公司为该险种至少支付10 000元赔偿金，则
发生当且仅当
， 
，
又
，故
．
（2）该险种总收入为
元，支出是赔偿金总额与成本的和．
支出 
，
盈利 
，
盈利的期望为 
，
由
知，
，
．
（元）．
故每位投保人应交纳的最低保费为15元．
21．（全国Ⅱ文）（19）．（本小题满分12分）
甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹．根据以往资料知，甲击中8环，9环，10环的概率分别为0.6，0.3，0.1，乙击中8环，9环，10环的概率分别为0.4，0.4，0.2．
设甲、乙的射击相互独立．
（1）求在一轮比赛中甲击中的环数多于乙击中环数的概率；
（2）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率．
解：记
分别表示甲击中9环，10环，
分别表示乙击中8环，9环，
表示在一轮比赛中甲击中的环数多于乙击中的环数，
表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数，
分别表示三轮中恰有两轮，三轮甲击中环数多于乙击中的环数．
（1）
，
．
（2）
，
，
，
．
22．（山东理）（18）（本小题满分12分）甲乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分。假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
（1）求随机变量ε分布列和数学期望；
(2) 用A表示“甲、乙两个队总得分之和等于3”这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).
(1)解法一：由题意知，ε的可能取值为0，1，2，3,且
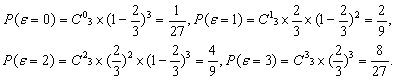
所以ε的分布列为
| ε | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
ε的数学期望为 Eε=
解法二：根据题设可知
因此ε的分布列为
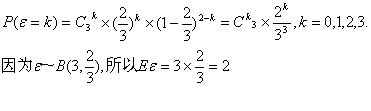
（2）解法一：用C表示“甲得2分乙得1分”这一事件，用D表示“甲得3分乙得0分”这一事件，所以AB=C∪D,且C、D互斥，又
由互斥事件的概率公式得
解法二：用Ak表示“甲队得k分”这一事件，用Bk表示“已队得k分”这一事件，k=0,1,2,3由于事件A3B0,A2B1为互斥事件，故事
P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
=
23．（山东文）18．（本小题满分12分）现有8名奥运会志愿者，其中志愿者
通晓日语，
通晓俄语，通晓韩语．从中选出通晓日语、俄语和韩语的志愿者各1名，组成一个小组．
（1）求
被选中的概率；
（2）求
和
不全被选中的概率．
解：（1）从8人中选出日语、俄语和韩语志愿者各1名，其一切可能的结果组成的基本事件空间
{
，
，
，
，
，
，
，
，
}
由18个基本事件组成．由于每一个基本事件被抽取的机会均等，因此这些基本事件的发生是等可能的．
用
表示“恰被选中”这一事件，则
{，
}
事件由6个基本事件组成，
因而
．
（2）用
表示“
不全被选中”这一事件，则其对立事件
表示“全被选中”这一事件，
由于
{
}，事件有3个基本事件组成，
所以
，由对立事件的概率公式得
．
24．（陕西理）（18）．（本小题满分12分）
某射击测试规则为：每人最多射击3次，击中目标即终止射击，第次击中目标得
分，3次均未击中目标得0分．已知某射手每次击中目标的概率为0.8，其各次射击结果互不影响．
（1）求该射手恰好射击两次的概率；
（2）该射手的得分记为，求随机变量的分布列及数学期望．
解：（1）设该射手第次击中目标的事件为
，则
，
．
（2）可能取的值为0，1，2，3． 的分布列为
|
| 0 | 1 | 2 | 3 |
|
| 0.008 | 0.032 | 0.16 | 0.8 |
25．（陕西文）18．（本小题满分12分）一个口袋中装有大小相同的2个红球,3个黑球和4个白球,从口袋中一次摸出一个球,摸出的球不再放回.
（1）连续摸球2次,求第一次摸出黑球,第二次摸出白球的概率；
（2）如果摸出红球,则停止摸球,求摸球次数不超过3次的概率．
解：（1）从袋中依次摸出2个球共有
种结果，第一次摸出黑球、第二次摸出白球有
种结果，则所求概率
．
（2）第一次摸出红球的概率为
，第二次摸出红球的概率为
，第三次摸出红球的概率为
，则摸球次数不超过3次的概率为
．
26．（四川理）（18）．（本小题满分12分） 设进入某商场的每一位顾客购买甲种商品的概率为
，购买乙种商品的概率为
，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的。
（1）求进入商场的1位顾客购买甲、乙两种商品中的一种的概率；
（2）求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率；
（3）记表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数，求的分布列及期望。
解：记表示事件：进入商场的1位顾客购买甲种商品，
记表示事件：进入商场的1位顾客购买乙种商品，
记
表示事件：进入商场的1位顾客购买甲、乙两种商品中的一种，
记
表示事件：进入商场的1位顾客至少购买甲、乙两种商品中的一种，
（1）
（2）
，
（3）
，故的分布列
，
，
所以
27．（四川文）（18）．（本小题满分12分）设进入某商场的每一位顾客购买甲商品的概率为0.5，购买乙商品的概率为0.6，且顾客购买甲商品与购买乙商品相互独立，各顾客之间购买商品是相互独立的.
(1)求进入该商场的1位顾客购买甲、乙两种商品中的一种的概率；
(2)求进入该商场的3位顾客中，至少有2位顾客既未购买甲种也未购买乙种商品的概率；
解：（1）记A表示事件：进入该商场的1位顾客选购甲种商品.
B表示事件：进入该商场的1位顾客选购乙种商品.
C表示事件：进入该商场的1位顾客选购甲、乙两种商品中的一种.
则
=
=
=0.5×0.4+0.5×0.6＝0.5.
（2）记A2表示事件：进入该商场的3位顾客中恰有2位顾客既未选购甲种商品，也未选购乙种商品.
A2表示事件：进入该商场的3位顾客中都未选购甲种商品，也未选购乙种商品.
D表示事件：进入该商场的1位顾客未选购甲种商品，也未选购乙种商品.
E表示事件：进入该商场的3位顾客中至少有2位顾客既未选购甲种商品，也未选购乙种商品.
则
28．（天津理）18．（本小题满分12分）甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球2次均未命中的概率为
．
（1）求乙投球的命中率；
（2）若甲投球1次，乙投球2次，两人共命中的次数记为，求的分布列和数学期望．
解：（1）设“甲投球一次命中”为事件，“乙投球一次命中”为事件，
由题意得
，
解得
或
（舍去），所以乙投球的命中率为．
（2）由题设和（Ⅰ）知
，
，
，
．
可能的取值为0，1，2，3，故
，
，
，
．
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
的数学期望
．
29．（天津文）18．（本小题满分12分）甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球2次均未命中的概率为．
（1）求乙投球的命中率；
（2）求甲投球2次，至少命中1次的概率；
（3）若甲、乙两人各投球2次，求两人共命中2次的概率．
（1）解法一：设“甲投球一次命中”为事件，“乙投球一次命中”为事件，由题意得，
解得或（舍去），所以乙投球的命中率为．
解法二：设“甲投球一次命中”为事件，“乙投球一次命中”为事件，由题意得
，
于是
或
（舍去），故
．
所以乙投球的命中率为．
（2）解法一：由题设和（Ⅰ）知，，．
故甲投球2次至少命中1次的概率为
．
解法二：由题设和（1）知，，．
故甲投球2次至少命中1次的概率为
．
（3）解：由题设和（1）知，，，，．
甲、乙两人各投球2次，共命中2次有三种情况：甲、乙两人各中一次；甲中2次，乙2次均不中；甲2次均不中，乙中2次．概率分别为
，
，
．
所以甲、乙两人各投球2次，共命中2次的概率为 
．
30．（浙江理）（19）．（本题14分）一个袋中装有若干个大小相同的黑球，白球和红球．已知从袋中任意摸出1个球，得到黑球的概率是；从袋中任意摸出2个球，至少得到1个白球的概率是
．
（1）若袋中共有10个球，（ⅰ）求白球的个数；（ⅱ）从袋中任意摸出3个球，记得到白球的个数为，求随机变量的数学期望
．
（2）求证：从袋中任意摸出2个球，至少得到1个黑球的概率不大于
．并指出袋中哪种颜色的球个数最少．
（1）解：（i）记“从袋中任意摸出两个球，至少得到一个白球”为事件A，设袋中白球的个数为，则
，得到
．故白球有5个．
（ii）随机变量的取值为0，1，2，3，分布列是
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
的数学期望
．
（2）证明：设袋中有
个球，其中
个黑球，由题意得
，
所以
，
，故
．
记“从袋中任意摸出两个球，至少有1个黑球”为事件B，则
．
所以白球的个数比黑球多，白球个数多于
，红球的个数少于
．
故袋中红球个数最少．
31．（浙江文）（19）（本小题满分14分）一个袋中装有大小相同的黑球、白球和红球。已知袋中共有10个球。从袋中任意摸出1个球，得到黑球的概率是；从袋中任意摸出2个球，至少得到1个白球的概率是
。求：
（1）从中任意摸出2个球，得到的都是黑球的概率；
（2）袋中白球的个数。
解：（1）由题意知，袋中黑球的个数为
．
记“从袋中任意摸出两个球，得到的都是黑球”为事件A，则
．
（2）记“从袋中任意摸出两个球，至少得到一个白球”为事件B，
设袋中白球的个数为，则
，得到．
32．（重庆理）（18）（本小题满分13分，（1）小问5分，（2）小问8分.）
甲、乙、丙三人按下面的规则进行乒乓球比赛：第一局由甲、乙参加而丙轮空，以后每一局由前一局的获胜者与轮空者进行比赛，而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为
，且各局胜负相互独立.求：
（1） 打满3局比赛还未停止的概率；
（2）比赛停止时已打局数的分别列与期望E.
解：令
分别表示甲、乙、丙在第k局中获胜.
（1）由独立事件同时发生与互斥事件至少有一个发生的概率公式知，打满3局比
赛还未停止的概率为
（2）的所有可能值为2，3，4，5，6，且
故有分布列
|
| 2 | 3 | 4 | 5 | 6 |
| P |
|
|
|
|
|
从而
（局）.
33. （重庆文）（18）（本小题满分13分，（1）小问8分，（2）小问5分.）
在每道单项选择题给出的4个备选答案中，只有一个是正确的.若对4道选择题中的每一道都任意选定一个答案，求这4道题中：
（1）恰有两道题答对的概率;
（2）至少答对一道题的概率.
解：视“选择每道题的答案”为一次试验，则这是4次独立重复试验，且每次试验中“选择正确”这一事件发生的概率为.
由独立重复试验的概率计算公式得：
(1)恰有两道题答对的概率为
(2)解法一：至少有一道题答对的概率为
解法二：至少有一道题答对的概率为
