09 排列组合二项式定理
一、选择题
1.(安徽7).设![]() 则
则![]() 中奇数的个数为( A )
中奇数的个数为( A )
A.2 B.3 C.4 D.5
2.(安徽12)12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是 ( C )
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
3.(福建9) 某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( A )
A.14 B.24 C.28 D.48
4.(湖南8)某市拟从4个重点项目和6个一般项目中各选2个项目作为本年度启动的项目,
则重点项目A和一般项目B至少有一个被选中的不同选法种数是 ( C )
A.15 B.45 C.60 D.75
5.(江西8)![]() 展开式中的常数项为( D )
展开式中的常数项为( D )
A.1 B.![]() C.
C.![]() D.
D.![]()
6.(辽宁10)一生产过程有4道工序,每道工序需要安排一人照看.现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案共有( B )
A.24种 B.36种 C.48种 D.72种
7.(全国Ⅰ3)![]() 的展开式中
的展开式中![]() 的系数为( C )
的系数为( C )
A.10 B.5 C.![]() D.1
D.1
8.(全国Ⅰ12)将1,2,3填入![]() 的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( B )
的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( B )
A.6种 B.12种 C.24种 D.48种

9.(全国Ⅱ9)![]() 的展开式中
的展开式中![]() 的系数是( A )
的系数是( A )
A.![]() B.
B.![]() C.3 D.4
C.3 D.4
10.(浙江6)在![]() 的展开式中,含
的展开式中,含![]() 的项的系数是 (
A )
的项的系数是 (
A )
(A)-15 (B)85 (C)-120 (D)274
11.(重庆10)若(x+![]() )n的展开式中前三项的系数成等差数,则展开式中x4项的系数为( B
)
)n的展开式中前三项的系数成等差数,则展开式中x4项的系数为( B
)
(A)6 (B)7 (C)8 (D)9
12.(湖北2.) ![]() 的展开式中常数项是 ( B
)
的展开式中常数项是 ( B
)
A.210
B.![]() C.
C.![]() D.-105
D.-105
13.(湖北9).从5名男生和5名女生中选3人组队参加某集体项目的比赛,其中至少有一名女生入选的组队方案数为 ( B )
A.100 B.110 C.120 D.180
14.(陕西12) 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为![]()
![]() (
(![]() ),传输信息为
),传输信息为![]() ,其中
,其中![]() ,
,![]() 运算规则为:
运算规则为:![]() ,
,![]() ,
,![]() ,
,![]() ,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( C )
,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( C )
A.11010 B.01100 C.10111 D.00011
二、填空题
1.(北京12)![]() 的展开式中常数项为______10;各项系数之和为_______.32(用数字作答)
的展开式中常数项为______10;各项系数之和为_______.32(用数字作答)
2.(福建13)(x+![]() )9展开式中x2的系数是
.84(用数字作答)
)9展开式中x2的系数是
.84(用数字作答)
3.(湖南13)记![]() 的展开式中第m项的系数为
的展开式中第m项的系数为![]() ,若
,若![]() ,则
,则![]() =__________.5
=__________.5
4.(湖南15)设![]() 表示不超x的最大整数,(如
表示不超x的最大整数,(如![]() )。对于给定的
)。对于给定的![]() ,
,
定义![]() 则
则![]() ________;
________;
当![]() 时,函数
时,函数![]() 的值域是_________________________。
的值域是_________________________。
![]()
![]()
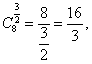 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
所以![]() 故函数
故函数![]() 的值域是
的值域是![]() .
.
5.(辽宁15)![]() 展开式中的常数项为
.35
展开式中的常数项为
.35
6.(全国Ⅱ14)从10名男同学,6名女同学中选3名参加体能测试,则选到的3名同学中既有男同学又有女同学的不同选法共有 种(用数字作答)420
7.(四川13)![]() 展开式中
展开式中![]() 的系数为______
的系数为______![]() _________。
_________。
8.(四川15)从甲、乙等10名同学中挑选4名参加某校公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有_______![]() _________种。
_________种。
9.(天津12) ![]() 的二项展开式中
的二项展开式中![]() 的系数为
(用数字作答).10
的系数为
(用数字作答).10
10.(天津16) 有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行.如果取出的4张卡片所标的数字之和等于10,则不同的排法共有 种(用数字作答).432
11.(浙江17)用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻,这样的六位数的个数是 (用数字作答)。40
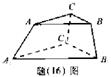
12.(重庆16)某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如题(16)图所示的6个点A、B、C、A1、B1、C1上各安装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有 种(用数字作答).12
13.(陕西14) ![]() 的展开式中
的展开式中![]() 的系数为
84 .(用数字作答)
的系数为
84 .(用数字作答)
14.(陕西16) 某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 96 种.(用数字作答).