03 数列
一、选择题
1.(北京7).已知等差数列![]() 中,
中,![]() ,
,![]() ,若
,若![]() ,则数列
,则数列![]() 的前5项和等于( C
)
的前5项和等于( C
)
A.30 B.45 C.90 D.186
2.(广东4)记等差数列{an}的前n项和为Sn,若S1=4,S4=20,则该数列的公差d= ( B )
A.7 B.6 C.3 D.2
3.(宁夏8)设等比数列![]() 的公比q=2,前n项和为Sn,则
的公比q=2,前n项和为Sn,则![]() =( C )
=( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.(江西5)在数列![]() 中,
中,![]() ,
, ![]() ,则
,则![]() ( A
)
( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(全国Ⅰ7)已知等比数列![]() 满足
满足![]() ,则
,则![]() ( A )
( A )
A.64 B.81 C.128 D.243
6.(福建3)设![]() 是等差数列,若
是等差数列,若![]() ,则数列
,则数列![]() 前8项和为( C )
前8项和为( C )
A.128 B.80 C.64 D.56
7.(上海14)若数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的无穷等比数列,且
的无穷等比数列,且![]() 各项的和为a,则
各项的和为a,则![]() 的值是( B )
的值是( B )
A.1 B.2
C.![]() D.
D.![]()
8.(天津4) 若等差数列![]() 的前5项和
的前5项和![]() ,且
,且![]() ,则
,则![]() ( B
)
( B
)
A.12 B.13 C.14 D.15
9.(浙江4)已知![]() 是等比数列,
是等比数列,![]() ,则公比
,则公比![]() = ( D )
= ( D )
(A)![]() (B)
(B)![]() (C)2
(D)
(C)2
(D)![]()
10.(重庆1)已知{an}为等差数列,a2+a8=12,则a5等于 ( C )
(A)4 (B)5 (C)6 (D)7
11.(陕西4) 已知![]() 是等差数列,
是等差数列,![]() ,
,![]() ,则该数列前10项和
,则该数列前10项和![]() 等于( B )
等于( B )
A.64 B.100 C.110 D.120
二、填空题
1.(安徽15) 在数列![]() 在中,
在中,![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为常数,则
为常数,则![]() -1
-1
2.(宁夏13)已知![]() 为等差数列,
为等差数列,![]() ,
,![]() ,则
,则![]() .15
.15
3.(江苏10)将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
。 。 。 。 。
按照以上排列的规律,第n行(![]() )从左向右的第3个数为
)从左向右的第3个数为 ![]()
4.(四川16)设数列![]() 中,
中,![]() ,
,
则通项![]() ______
______![]() _____。
_____。
三、解答题
1.(安徽21)(本小题满分12分)
设数列![]() 满足
满足![]() 其中
其中![]() 为实数,且
为实数,且![]()
(Ⅰ)求数列![]() 的通项公式
的通项公式
(Ⅱ)设![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)若![]() 对任意
对任意![]() 成立,证明
成立,证明![]()
解 (1) 方法一:
![]()
![]() 当
当![]() 时,
时,![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列。
的等比数列。
![]() ,即
,即 ![]() 。当
。当![]() 时,
时,![]() 仍满足上式。
仍满足上式。
![]() 数列
数列![]() 的通项公式为
的通项公式为 ![]()
![]() 。
。
方法二
由题设得:当![]() 时,
时,
![]()
![]()
![]() 时,
时,![]() 也满足上式。
也满足上式。
![]() 数列
数列![]() 的通项公式为
的通项公式为 ![]()
![]() 。
。
(2) 由(1)得![]()
![]()
![]()
![]()
![]()
![]()
(3) 由(1)知![]()
若![]() ,则
,则![]()
![]()
![]()
由![]() 对任意
对任意![]() 成立,知
成立,知![]() 。下面证
。下面证![]() ,用反证法
,用反证法
方法一:假设![]() ,由函数
,由函数![]() 的函数图象知,当
的函数图象知,当![]() 趋于无穷大时,
趋于无穷大时,![]() 趋于无穷大
趋于无穷大
![]() 不能对
不能对![]() 恒成立,导致矛盾。
恒成立,导致矛盾。![]() 。
。
![]()
方法二:假设![]() ,
,![]() ,
,![]()
即 ![]() 恒成立 (*)
恒成立 (*)
![]() 为常数,
为常数,![]() (*)式对
(*)式对![]() 不能恒成立,导致矛盾,
不能恒成立,导致矛盾,![]()
![]()
2.(北京20)(本小题共13分)
数列![]() 满足
满足![]() ,
,![]() (
(![]() ),
),![]() 是常数.
是常数.
(Ⅰ)当![]() 时,求
时,求![]() 及
及![]() 的值;
的值;
(Ⅱ)数列![]() 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(Ⅲ)求![]() 的取值范围,使得存在正整数
的取值范围,使得存在正整数![]() ,当
,当![]() 时总有
时总有![]() .
.
解:(Ⅰ)由于![]() ,且
,且![]() .
.
所以当![]() 时,得
时,得![]() ,
,
故![]() .
.
从而![]() .
.
(Ⅱ)数列![]() 不可能为等差数列,证明如下:
不可能为等差数列,证明如下:
由![]() ,
,![]() 得
得
![]() ,
,![]() ,
,![]() .
.
若存在![]() ,使
,使![]() 为等差数列,则
为等差数列,则![]() ,即
,即![]() ,
,
解得![]() .
.
于是![]() ,
,![]() .
.
这与![]() 为等差数列矛盾.所以,对任意
为等差数列矛盾.所以,对任意![]() ,
,![]() 都不可能是等差数列.
都不可能是等差数列.
(Ⅲ)记![]() ,根据题意可知,
,根据题意可知,![]() 且
且![]() ,即
,即![]() 且
且![]() ,这时总存在
,这时总存在![]() ,满足:当
,满足:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以由![]() 及
及![]() 可知,若
可知,若![]() 为偶数,则
为偶数,则![]() ,从而当
,从而当![]() 时,
时,![]() ;若
;若![]() 为奇数,则
为奇数,则![]() ,从而当
,从而当![]() 时
时![]() .
.
因此“存在![]() ,当
,当![]() 时总有
时总有![]() ”的充分必要条件是:
”的充分必要条件是:![]() 为偶数,
为偶数,
记![]() ,则
,则![]() 满足
满足
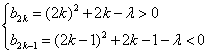 .
.
故![]() 的取值范围是
的取值范围是![]() .
.
3.(福建20)(本小题满分12分)
已知{an}是正数组成的数列,a1=1,且点(![]() )(n
)(n![]() N*)在函数y=x2+1的图象上.
N*)在函数y=x2+1的图象上.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若列数{bn}满足b1=1,bn+1=bn+![]() ,求证:bn ·bn+2<b2n+1.
,求证:bn ·bn+2<b2n+1.
解法一:
(Ⅰ)由已知得an+1=an+1、即an+1-an=1,又a1=1,
所以数列{an}是以1为首项,公差为1的等差数列.
故an=1+(a-1)×1=n.
(Ⅱ)由(Ⅰ)知:an=n从而bn+1-bn=2n.
bn=(bn-bn-1)+(bn-1-bn-2)+···+(b2-b1)+b1
=2n-1+2n-2+···+2+1
=![]() =2n-1.
=2n-1.
因为bn·bn+2-b![]() =(2n-1)(2n+2-1)-(2n-1-1)2
=(2n-1)(2n+2-1)-(2n-1-1)2
=(22n+2-2n+2-2n+1)-(22n+2-2-2n+1-1)
=-5·2n+4·2n
=-2n<0,
所以bn·bn+2<b![]() ,
,
解法二:
(Ⅰ)同解法一.
(Ⅱ)因为b2=1,
bn·bn+2- b![]() =(bn+1-2n)(bn+1+2n+1)-
b
=(bn+1-2n)(bn+1+2n+1)-
b![]()
=2n+1·bn-1-2n·bn+1-2n·2n+1
=2n(bn+1-2n+1)
=2n(bn+2n-2n+1)
=2n(bn-2n)
=…
=2n(b1-2)
=-2n〈0,
所以bn-bn+2<b2n+1
4.(广东21)(本小题满分14分)
设数列{an}满足a1=1,a2=2,an=![]() (an-1+2an-2)(n=3,4,…),数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1
(an-1+2an-2)(n=3,4,…),数列{bn}满足b1=1,bn(n=2,3,…)是非零整数,且对任意的正整数m和自然数k,都有-1![]() bm+bm+1+…+bm+1
bm+bm+1+…+bm+1![]() 1.
1.
(1)求数列{an}和{bn}的通项公式;
(2) 记cn=nanbn(n=1,2,…),求数列{cn}的前n项和Sn.
解:(1)由![]() 得
得 ![]()
![]()
又 ![]() ,
,
![]() 数列
数列![]() 是首项为1公比为
是首项为1公比为![]() 的等比数列,
的等比数列,
![]()
![]()
![]()
 ,
,
由 得
得
![]() ,由
,由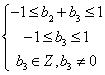 得
得
![]() ,…
,…
同理可得当n为偶数时,![]() ;当n为奇数时,
;当n为奇数时,![]() ;
;
|
|
|
|
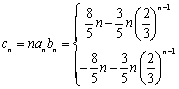
![]()
当n为奇数时,
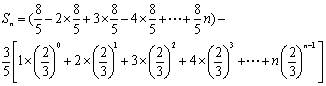
![]()
当n为偶数时,
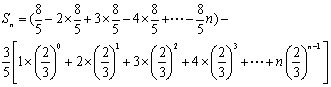
![]()
![]()
令![]() ……①
……①
①×![]() 得:
得: ![]() ……②
……②
①-②得: ![]()
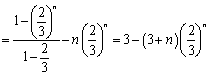
![]()
![]()
|
|
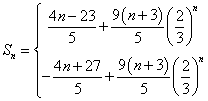
5.(江苏19)(16分)
(1)设![]() 是各项均不为零的等差数列(
是各项均不为零的等差数列(![]() ),且公差
),且公差![]() ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
①当![]() 时,求
时,求![]() 的数值;②求
的数值;②求![]() 的所有可能值;
的所有可能值;
(2)求证:对于一个给定的正整数![]() ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列![]() ,其中任意三项(按原来顺序)都不能组成等比数列。
,其中任意三项(按原来顺序)都不能组成等比数列。
【解析】:本小题考查等差数列、等比数列的综合应用。
(1)①当n=4时, ![]() 中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。
中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0。
若删去![]() ,则
,则![]() ,即
,即![]() 化简得
化简得![]() ,得
,得![]()
若删去![]() ,则
,则![]() ,即
,即![]() 化简得
化简得![]() ,得
,得![]()
综上,得![]() 或
或![]() 。
。
②当n=5时, ![]() 中同样不可能删去
中同样不可能删去![]() ,否则出现连续三项。
,否则出现连续三项。
若删去![]() ,则
,则![]() ,即
,即![]() 化简得
化简得![]() ,因为
,因为![]() ,所以
,所以![]() 不能删去;
不能删去;
当n≥6时,不存在这样的等差数列。事实上,在数列![]() 中,由于不能删去首项或末项,若删去
中,由于不能删去首项或末项,若删去![]() ,则必有
,则必有![]() ,这与
,这与![]() 矛盾;同样若删去
矛盾;同样若删去![]() 也有
也有![]() ,这与
,这与![]() 矛盾;若删去
矛盾;若删去![]() 中任意一个,则必有
中任意一个,则必有![]() ,这与
,这与![]() 矛盾。(或者说:当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)
矛盾。(或者说:当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)
综上所述,![]() 。
。
(2)假设对于某个正整数n,存在一个公差为d的n项等差数列![]() ,其中
,其中![]() (
(![]() )为任意三项成等比数列,则
)为任意三项成等比数列,则![]() ,即
,即![]() ,化简得
,化简得![]() (*)
(*)
由![]() 知,
知,![]() 与
与![]() 同时为0或同时不为0
同时为0或同时不为0
当![]() 与
与![]() 同时为0时,有
同时为0时,有![]() 与题设矛盾。
与题设矛盾。
故![]() 与
与![]() 同时不为0,所以由(*)得
同时不为0,所以由(*)得![]()
因为![]() ,且x、y、z为整数,所以上式右边为有理数,从而
,且x、y、z为整数,所以上式右边为有理数,从而![]() 为有理数。
为有理数。
于是,对于任意的正整数![]() ,只要
,只要![]() 为无理数,相应的数列就是满足题意要求的数列。
为无理数,相应的数列就是满足题意要求的数列。
例如n项数列1,![]() ,
,![]() ,……,
,……,![]() 满足要求。
满足要求。
6.(江西19)等差数列![]() 的各项均为正数,
的各项均为正数,![]() ,前
,前![]() 项和为
项和为![]() ,
,![]() 为等比数列,
为等比数列, ![]() ,且
,且![]()
![]() .
.
(1)求![]() 与
与![]() ;
;
(2)求和:![]() .
.
(1)设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,则
,则![]() 为正整数,
为正整数,
![]() ,
,![]()
依题意有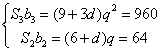 ①
①
解得![]() 或
或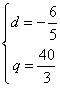 (舍去)
(舍去)
故![]()
(2)![]()
∴![]()
![]()
![]()
![]()
7.(湖南20)数列![]() 满足
满足
![]()
![]()
(I)求![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(II)设![]() ,
,![]() ,
,![]() ,
,
求使![]() 的所有k的值,并说明理由。
的所有k的值,并说明理由。
解:(I)因为![]() 所以
所以![]()
![]() 一般地, 当
一般地, 当![]() 时,
时,
![]()
即![]() 所以数列
所以数列![]() 是首项为0、公差为4的等差数列,
是首项为0、公差为4的等差数列,
因此![]()
当![]() 时,
时,![]()
所以数列![]() 是首项为2、公比为2的等比数列,因此
是首项为2、公比为2的等比数列,因此![]()
故数列![]() 的通项公式为
的通项公式为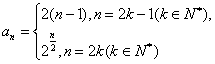
(II)由(I)知,![]()
![]()
![]()
于是![]()
![]()
![]()
![]()
![]()
![]() .
.
下面证明:
当![]() 时,
时,![]() 事实上, 当
事实上, 当![]() 时,
时,
![]() 即
即![]()
又![]() 所以当
所以当![]() 时,
时,![]()
故满足![]() 的所有k的值为3,4,5.
的所有k的值为3,4,5.
8.(辽宁20)(本小题满分12分)
在数列![]() ,
,![]() 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设![]() .
.
(Ⅰ)数列![]() 是否为等比数列?证明你的结论;
是否为等比数列?证明你的结论;
(Ⅱ)设数列![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() .若
.若![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
解:(Ⅰ)![]() 是等比数列.·························································································· 2分
是等比数列.·························································································· 2分
证明:设![]() 的公比为
的公比为![]() ,
,![]() 的公比为
的公比为![]() ,则
,则
![]() ,故
,故![]() 为等比数列.··········································· 5分
为等比数列.··········································· 5分
(Ⅱ)数列![]() 和
和![]() 分别是公差为
分别是公差为![]() 和
和![]() 的等差数列.
的等差数列.
由条件得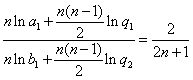 ,即
,即
![]() .···················································································· 7分
.···················································································· 7分
故对![]() ,
,![]() ,…,
,…,
![]() .
.
于是
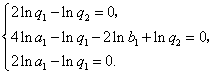
将![]() 代入得
代入得![]() ,
,![]() ,
,![]() .································································ 10分
.································································ 10分
从而有![]() .
.
所以数列![]() 的前
的前![]() 项和为
项和为
![]() .····················································································· 12分
.····················································································· 12分
9.(全国Ⅰ19)(本小题满分12分)
在数列![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)设![]() .证明:数列
.证明:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
解:(1)![]() ,
,
![]() ,
,
![]() ,
,
则![]() 为等差数列,
为等差数列,![]() ,
,
![]() ,
,![]() .
.
(2)![]()
![]()
两式相减,得
![]() .
.
10.(全国Ⅱ18)(本小题满分12分)
等差数列![]() 中,
中,![]() 且
且![]() 成等比数列,求数列
成等比数列,求数列![]() 前20项的和
前20项的和![]() .
.
解:设数列![]() 的公差为
的公差为![]() ,则
,则
![]() ,
,
![]() ,
,
![]() .····························································································· 3分
.····························································································· 3分
由![]() 成等比数列得
成等比数列得![]() ,
,
即![]() ,
,
整理得![]() ,
,
解得![]() 或
或![]() .···································································································· 7分
.···································································································· 7分
当![]() 时,
时,![]() .················································································· 9分
.················································································· 9分
当![]() 时,
时,![]() ,
,
于是![]()
![]() .····················································· 12分
.····················································· 12分
11.(山东20)(本小题满分12分)
将数列![]() 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
记表中的第一列数![]() 构成的数列为
构成的数列为![]() ,
,![]() .
.![]() 为数列
为数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() .
.
(Ⅰ)证明数列![]() 成等差数列,并求数列
成等差数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当![]() 时,求上表中第
时,求上表中第![]() 行所有项的和.
行所有项的和.
(Ⅰ)证明:由已知,当![]() 时,
时,![]() ,
,
又![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() ,
,
又![]() .
.
所以数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列.
的等差数列.
由上可知![]() ,
,
即![]() .
.
所以当![]() 时,
时,![]() .
.
因此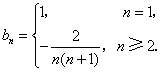
(Ⅱ)解:设上表中从第三行起,每行的公比都为![]() ,且
,且![]() .
.
因为![]() ,
,
所以表中第1行至第12行共含有数列![]() 的前78项,
的前78项,
故![]() 在表中第13行第三列,
在表中第13行第三列,
因此![]() .
.
又![]() ,
,
所以![]() .
.
记表中第![]() 行所有项的和为
行所有项的和为![]() ,
,
则![]() .
.
12.(上海21)(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 是正整数),与数列
是正整数),与数列
![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 是正整数).
是正整数).
记![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求证:当![]() 是正整数时,
是正整数时,![]() ;
;
(3)已知![]() ,且存在正整数
,且存在正整数![]() ,使得在
,使得在![]() ,
,![]() ,
,![]() ,
,![]() 中有4项为100.求
中有4项为100.求![]() 的值,并指出哪4项为100.
的值,并指出哪4项为100.
【解】(1)![]()
![]() ………………..2分
………………..2分
∵ ![]() ………………..4分
………………..4分
【证明】(2)用数学归纳法证明:当![]()
①
当n=1时,![]() 等式成立….6分
等式成立….6分
②
假设n=k时等式成立,即![]()
那么当![]() 时,
时,
![]() ………8分
………8分
![]()
![]() 等式也成立.
等式也成立.
根据①和②可以断定:当![]() …………………...10分
…………………...10分
【解】(3)
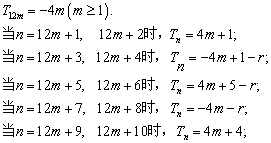
![]() ………………………..13分
………………………..13分
∵ 4m+1是奇数,![]() 均为负数,
均为负数,
∴ 这些项均不可能取到100. ………………………..15分
此时,![]() 为100.
…………………………18分
为100.
…………………………18分
13.(四川21)(本小题满分12分)
设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
(Ⅰ)求![]()
(Ⅱ)证明: ![]() 是等比数列;
是等比数列;
(Ⅲ)求![]() 的通项公式
的通项公式
【解】:(Ⅰ)因为![]() ,所以
,所以![]()
由![]() 知
知
![]()
![]()
得![]() ①
①
所以![]()
![]()
![]()
(Ⅱ)由题设和①式知
![]()
![]()
![]()
所以![]() 是首项为2,公比为2的等比数列。
是首项为2,公比为2的等比数列。
(Ⅲ)![]()
![]()
14.(天津20)(本小题满分12分)
已知数列![]() 中,
中,![]() ,
,![]() ,且
,且![]()
![]() .
.
(Ⅰ)设![]() ,证明
,证明![]() 是等比数列;
是等比数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ)若![]() 是
是![]() 与
与![]() 的等差中项,求
的等差中项,求![]() 的值,并证明:对任意的
的值,并证明:对任意的![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(Ⅰ)证明:由题设![]() ,得
,得
![]() ,
,
即
![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(Ⅱ)解:由(Ⅰ),
![]() ,
,
![]() ,
,
……
![]() .
.
将以上各式相加,得![]() .所以当
.所以当![]() 时,
时,
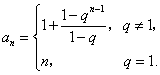
上式对![]() 显然成立.
显然成立.
(Ⅲ)解:由(Ⅱ),当![]() 时,显然
时,显然![]() 不是
不是![]() 与
与![]() 的等差中项,故
的等差中项,故![]() .
.
由![]() 可得
可得![]() ,由
,由![]() 得
得
![]() , ①
, ①
整理得![]() ,解得
,解得![]() 或
或![]() (舍去).于是
(舍去).于是
![]() .
.
另一方面,
![]() ,
,
![]() .
.
由①可得
![]() .
.
所以对任意的![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
15.(浙江18)(本题14分)已知数列![]() 的首项
的首项![]() ,通项
,通项![]() (
(![]() 为常数),且
为常数),且![]() 成等差数列,求:
成等差数列,求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ)数列![]() 的前
的前![]() 项的和
项的和![]() 的公式。
的公式。
(Ⅰ)解:由![]() ,得
,得![]() ,
,
又![]() ,
,![]() ,且
,且![]() ,得
,得
![]() ,
,
解得![]() ,
,![]() .
.
(Ⅱ)解:![]()
![]() .
.
16.(重庆22)(本小题满分12分,(Ⅰ)小问6分.(Ⅱ)小问6分)
设各项均为正数的数列{an}满足![]() .
.
(Ⅰ)若![]() 求a3,a4,并猜想a2008的值(不需证明);
求a3,a4,并猜想a2008的值(不需证明);
(Ⅱ)若![]() 对n≥2恒成立,求a2的值.
对n≥2恒成立,求a2的值.
解:(I)因a1=2,a2=2-2,故
![]()
![]()
由此有a1=2(-2)0, a2=2(-2)4, a3=2(-2)2, a4=2(-2)3,
从而猜想an的通项为
![]() ,
,
所以a2xn=![]() .
.
(Ⅱ)令xn=log2an.则a2=2x2,故只需求x2的值。
设Sn表示x2的前n项和,则a1a2…an=![]() ,由2
,由2![]() ≤a1a2…an<4得
≤a1a2…an<4得
![]() ≤Sn=x1+x2+…+xn<2(n≥2).
≤Sn=x1+x2+…+xn<2(n≥2).
因上式对n=2成立,可得![]() ≤x1+x2,又由a1=2,得x1=1,故x2≥
≤x1+x2,又由a1=2,得x1=1,故x2≥![]() .
.
由于a1=2,![]() (n∈N*),得
(n∈N*),得![]() (n∈N*),即
(n∈N*),即
![]() ,
,
因此数列{xn+1+2xn}是首项为x2+2,公比为![]() 的等比数列,故
的等比数列,故
xn+1+2xn=(x2+2)![]() (n∈N*).
(n∈N*).
将上式对n求和得
Sn+1-x1+2Sn=(x2+2)(1+![]() +…+
+…+![]() )=(x2+2)(2-
)=(x2+2)(2-![]() )(n≥2).
)(n≥2).
因Sn<2,Sn+1<2(n≥2)且x1=1,故
(x2+2)(2-![]() )<5(n≥2).
)<5(n≥2).
因此2x2-1<![]() (n≥2).
(n≥2).
下证x2≤![]() ,若淆,假设x2>
,若淆,假设x2>![]() ,则由上式知,不等式
,则由上式知,不等式
2n-1<![]()
对n≥2恒成立,但这是不可能的,因此x2≤![]() .
.
又x2≥![]() ,故z2=
,故z2=![]() ,所以a2=2
,所以a2=2![]() =
=![]() .
.
17.(湖北21).(本小题满分14分)
已知数列![]()
![]() ,其中
,其中![]() 为实数,
为实数,![]() 为正整数.
为正整数.
(Ⅰ)证明:当![]()
(Ⅱ)设![]() 为数列
为数列![]() 的前n项和,是否存在实数
的前n项和,是否存在实数![]() ,使得对任意正整数n,都有
,使得对任意正整数n,都有
![]() 若存在,求
若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(Ⅰ)证明:假设存在一个实数l,使{an}是等比数列,则有![]() ,即
,即
(![]() )2=
)2=![]() 2
2![]() 矛盾.
矛盾.
所以{an}不是等比数列.
(Ⅱ)证明:∵![]()
![]()
![]()
![]()
![]() 又
又![]() 由上式知
由上式知![]()
![]() 故当
故当![]() 数列{bn}是以
数列{bn}是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅲ)当![]() 由(Ⅱ)得
由(Ⅱ)得![]() 于是
于是
![]()
![]()
当![]() 时,
时,![]() ,从而
,从而![]() 上式仍成立.
上式仍成立.
要使对任意正整数n , 都有![]()
即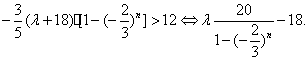
令![]()
当n为正奇数时,![]() 当n为正偶数时,
当n为正偶数时,![]()
![]()
于是可得![]()
综上所述,存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]()
![]()
![]() 的取值范围为
的取值范围为![]()
18.(陕西20)(本小题满分12分)
已知数列![]() 的首项
的首项![]() ,
,![]() ,
,![]() ….
….
(Ⅰ)证明:数列![]() 是等比数列;
是等比数列;
(Ⅱ)数列![]() 的前
的前![]() 项和
项和![]() .
.
解:(Ⅰ)![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() ,又
,又![]() ,
,![]()
![]() ,
,
![]() 数列
数列![]() 是以为
是以为![]() 首项,
首项,![]() 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)知![]() ,即
,即![]() ,
,![]()
![]() .
.
设![]() …
…![]() , ①
, ①
则![]() …
…![]() ,②
,②
由①![]() ②得
②得
![]() …
…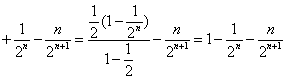 ,
,
![]()
![]() .又
.又![]() …
…![]() .
.
![]() 数列
数列![]() 的前
的前![]() 项和
项和 ![]() .
.