高二数学下学期期末复习题(五) 08年07月
一、填空题。
1.
若![]() ,则实数
,则实数![]() 。
。
2.
设函数 ,已知
,已知![]() ,则
,则![]() 的取值范围为_________.
的取值范围为_________.
3.
函数![]() 在点M(1,0)处的切线方程是 .
在点M(1,0)处的切线方程是 .
4. 函数y=log0.5(-2x2+5x-2)单调递增区间是 .
5.
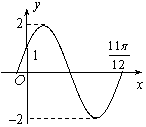 函数y=Asin(ωx+φ)(其中A>0,ω>0,φ<)
函数y=Asin(ωx+φ)(其中A>0,ω>0,φ<)
在一个周期内的图像如图所示.则函数解析
式为:_________________.
6.
设函数f (x)=kx3+3(k-1)x2-k2+1在区间(0,4)
上是减函数,则![]() 的取值范围是______________.
的取值范围是______________.
7. 如果复数z满足+=2,那么的最小值为_________.
8.
设命题p:4x-3≤1; q:![]() ≤0.若﹁ p是﹁
q的必要而不充分的条件,则实数a的取值范围是
.
≤0.若﹁ p是﹁
q的必要而不充分的条件,则实数a的取值范围是
.
9.
已知0<α<![]() ,-
,-![]() <β<0,cos(α-β)=
<β<0,cos(α-β)=![]() ,且tanα=
,且tanα=![]() ,则sinβ=_____.
,则sinβ=_____.
10. 已知f (x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为___________________.
11.
若偶函数![]() 在区间[-1,0]上是减函数,
在区间[-1,0]上是减函数,![]() ,
,![]() 是锐角三角形的两个内角,且
是锐角三角形的两个内角,且![]() ≠
≠![]() ,则
,则![]() 的大小关系为:_______________。
的大小关系为:_______________。
12.
若2sin2![]() +sin2
+sin2![]() =3sin
=3sin![]() ,则sin2
,则sin2![]() +sin2
+sin2![]() 的取值范围是_____________
的取值范围是_____________
13.
已知f (x)=x+lg(![]() ),若
),若![]() 恒成立,则m的取值范围是
.
恒成立,则m的取值范围是
.
14. 已知f (x)是偶函数,且f (x)在(0,+∞)上单调递增,若当x∈[,1]时,
f (ax+1)≤f (x-2)恒成立,则实数a的取值范围是
.
二、解答题
15. 已知![]() ,
,![]() ,分别就下面条件求
,分别就下面条件求![]() 的取值范围:
的取值范围:
(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
16. 已知函数![]() (
(![]() )的最小值正周期是
)的最小值正周期是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的最大值,并且求使
的最大值,并且求使![]() 取得最大值的
取得最大值的![]() 的集合.
的集合.
17.
已知函数f (x)=1-
(1)求g(a)的表达式;
(2)若g(a)=,求实数a的值及此时f (x)的最大值.
18.  如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,AB=
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,AB=
(I)要使矩形AMPN的面积大于32平方米,
则AN的长应在什么范围内?
(II) 若AN的长度不少于
是多少时,矩形AMPN的面积最小?并求出最小面积.
19.
设函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明:曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
20. 设函数![]() ,已知
,已知![]() 和
和![]() 为
为![]() 的极值点.
的极值点.
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)讨论![]() 的单调性;
的单调性;
(Ⅲ)设![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
高二期末复习题(五)答案 08年07月
21. 若![]() ,则实数
,则实数![]() 。-1
。-1
22.
设函数 ,已知
,已知![]() ,则
,则![]() 的取值范围为_________.
的取值范围为_________.
23.
函数![]() 在点M(1,0)处的切线方程是 .
在点M(1,0)处的切线方程是 .
24. 函数y=log0.5(-2x2+5x-2)单调递增区间是 .
25.
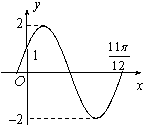 函数y=Asin(ωx+φ)(其中A>0,ω>0,φ<)在一个周期内的图像如图所示.则函数解析式为:_________________.
函数y=Asin(ωx+φ)(其中A>0,ω>0,φ<)在一个周期内的图像如图所示.则函数解析式为:_________________.
y=2sin(2x+)
26. 设函数f (x)=kx3+3(k-1)x2-k2+1在区间(0,4)上是减函数,则![]() 的取值范围是___________________.0≤k<
的取值范围是___________________.0≤k<
27. 如果复数z满足+=2,那么的最小值为_________.
28. 设命题p:4x-3≤1; q:![]() ≤0.若﹁ p是﹁
q的必要而不充分的条件,则实数a的取值范围是
.
≤0.若﹁ p是﹁
q的必要而不充分的条件,则实数a的取值范围是
.
[0,![]() ]
]
29. 已知0<α<![]() ,-
,-![]() <β<0,cos(α-β)=
<β<0,cos(α-β)=![]() ,且tanα=
,且tanα=![]() ,则sinβ=_________.-
,则sinβ=_________.-
30. 已知f (x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为___________________.a<-3或a>6
31.
若偶函数![]() 在区间[-1,0]上是减函数,
在区间[-1,0]上是减函数,![]() ,
,![]() 是锐角三角形的两个内角,且
是锐角三角形的两个内角,且![]() ≠
≠![]() ,则
,则![]() 的大小关系为:_______________。
的大小关系为:_______________。
32. 若2sin2a+sin2b=3sina,则sin2a+sin2b的取值范围是______________[0,]Ç{2}
33.
已知f (x)=x+lg(![]() ),若
),若![]() 恒成立,则m的取值范围是
.
恒成立,则m的取值范围是
.
34. 已知f (x)是偶函数,且f (x)在(0,+∞)上单调递增,若当xÎ[,1]时,f (ax+1)≤f
(x-2)恒成立,则实数a的取值范围是
.
[-2,0]【提示】对xÎ[,1],ax+1≤x-2∴ax+1≤2-x∴x-2≤ax+1≤2-x∴x-3≤ax≤1-x,xÎ[,1] 恒成立∴1-≤a≤-1对xÎ[,1]恒成立.下略.
35. 已知![]() ,
,![]() ,分别就下面条件求
,分别就下面条件求![]() 的取值范围:
的取值范围:
(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
解:(Ⅰ)(1)![]()
![]() ,
,![]() .
.
由![]() 有
有![]() 得
得![]() 与
与![]() ,矛盾!故当
,矛盾!故当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
(Ⅱ)![]() ,
,
![]() ,
,![]()
由![]() 必有
必有![]() ,∴
,∴![]() 或
或![]()
∴![]() (舍去)或
(舍去)或![]() 得
得![]()
故当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() .
.
36. 已知函数![]() (
(![]() )的最小值正周期是
)的最小值正周期是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的最大值,并且求使
的最大值,并且求使![]() 取得最大值的
取得最大值的![]() 的集合.
的集合.
解:(Ⅰ)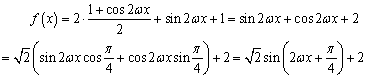
由题设,函数![]() 的最小正周期是
的最小正周期是![]() ,可得
,可得![]() ,所以
,所以![]() .
.
(Ⅱ)由(Ⅰ)知,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 取得最大值1,所以函数
取得最大值1,所以函数![]() 的最大值是
的最大值是![]() ,此时
,此时![]() 的集合为
的集合为![]() .
.
37.
已知函数f (x)=1-
(1)求g(a)的表达式;
(2)若g(a)=,求实数a的值及此时f (x)的最大值.
解:f (x)=2cos2x-2acosx-
(1)①当≤-1,即a≤-2时,g(a)=f (-1)=1;②当≥1,即a≥2时,g(a)=f (1)=1-
③当-1≤≤1,即-2≤a≤2时,g(a)=f ()=-;
(2)g(a)=Þa=1;ymax=f (1)=1-
38.  如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,AB=
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,AB=
(I)要使矩形AMPN的面积大于32平方米,
则AN的长应在什么范围内?
(II) 若AN的长度不少于
是多少时,矩形AMPN的面积最小?并求出最小面积.
解:设AN的长为x米(x >2) ∵![]() ,∴AM=
,∴AM=![]()
∴SAMPN=AN•AM=![]()
(I)由SAMPN >
32 得 ![]() > 32 ,∵x >2,∴
> 32 ,∵x >2,∴![]() ,
,
即(3x-8)(x-8)> 0 ∴![]()
即AN长的取值范围是![]()
(II) 令y=![]() ,则y′=
,则y′=![]()
∴当x > 4,y′> 0,即函数y=![]() 在(4,+∞)上单调递增,
在(4,+∞)上单调递增,
∴函数y=![]() 在[6,+∞]上也单调递增。
在[6,+∞]上也单调递增。
∴当x=6时y=![]() 取得最小值即SAMPN取得最小值27(平方米) 此时AN=
取得最小值即SAMPN取得最小值27(平方米) 此时AN=
39.
设函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明:曲线![]() 上任一点处的切线与直线
上任一点处的切线与直线![]() 和直线
和直线![]() 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
解:(Ⅰ)方程![]() 可化为
可化为![]() .当
.当![]() 时,
时,![]() .
.
又![]() ,于是
,于是 解得
解得![]() 故
故![]() .
.
(Ⅱ)设![]() 为曲线上任一点,由
为曲线上任一点,由![]() 知曲线在点
知曲线在点![]() 处的切线方程为
处的切线方程为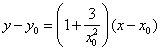 ,即
,即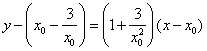 .
.
令![]() 得
得![]() ,从而得切线与直线
,从而得切线与直线![]() 的交点坐标为
的交点坐标为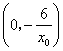 .
.
令![]() 得
得![]() ,从而得切线与直线
,从而得切线与直线![]() 的交点坐标为
的交点坐标为![]() .
.
所以,围成的三角形面积为![]() .
.
40. 设函数![]() ,已知
,已知![]() 和
和![]() 为
为![]() 的极值点.
的极值点.
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)讨论![]() 的单调性;
的单调性;
(Ⅲ)设![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
解:(Ⅰ)因为![]()
![]() ,
,
又![]() 和
和![]() 为
为![]() 的极值点,所以
的极值点,所以![]() ,
,
因此![]() 解方程组得
解方程组得![]() ,
,![]() .
.
(Ⅱ)因为![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .因为当
.因为当![]()
![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 和
和![]() 上是单调递增的;在
上是单调递增的;在![]() 和
和![]() 上是单调递减的.
上是单调递减的.
(Ⅲ)由(Ⅰ)可知![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() .令
.令![]() ,得
,得![]() ,
,
因为![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
故![]() 时,
时,![]() ;
;
因为![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
故![]() 时,
时,![]() .
.
所以对任意![]() ,恒有
,恒有![]() ,又
,又![]() ,
,
因此![]() ,
,
故对任意![]() ,恒有
,恒有![]() .
.