高二数学圆的方程练习
【同步达纲练习】
A级
一、选择题
1.若直线4x-3y-2=0与圆x2+y2-2ax+4y+a2-12=0总有两个不同交点，则a的取值范围是( )
A.-3＜a＜7 B.-6＜a＜4
C.-7＜a＜3 D.-21＜a＜19
2.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有( )
A.1个 B.2个 C.3个 D.4个
3.使圆(x-2)2+(y+3)2=2上点与点(0，-5)的距离最大的点的坐标是( )
A.(5，1) B.(3，-2)
C.(4，1) D.(
+2，-3)
4.若直线x+y=r与圆x2+y2=r(r＞0)相切，则实数r的值等于( )
A.
B.1 C.
D.2
5.直线x-y+4=0被圆x2+y2+4x-4y+6=0截得的弦长等于( )
A.8 B.4 C.2 D.4
二、填空题
6.过点P(2，1)且与圆x2+y2-2x+2y+1=0相切的直线的方程为 .
7.设集合m={(x,y)x2+y2≤25,N={(x,y)｜(x-a)2+y2≤9}，若M∪N=M，则实数a的取值范围是 .
8.已知P(3，0)是圆x2+y2-8x-2y+12=0内一点则过点P的最短弦所在直线方程是 ，过点P的最长弦所在直线方程是 .
三、解答题
9.已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点，若OP⊥OQ(O是原点)，求m的值.
10.已知直线l:y=k(x-2)+4与曲线C：y=1+
有两个不同的交点，求实数k的取值范围.
AA级
一、选择题
1.圆(x-3)2+(y+4)2=2关于直线x+y=0的对称圆的标准方程是( )
A.(x+3)2+(y-4)2=2 B.(x-4)2+(y+3)2=2
C.(x+4)2+(y-3)=2 D.(x-3)2+(y-4)2=2
2.点P(5a+1,12a)在圆(x-1)2+y2=1的内部，则实数a的取值范围是( )
A.｜a｜＜1 B.｜a｜＜
C.｜a｜＜
D.｜a｜＜
3.关于x,y的方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示一个圆的充要条件是( )
A.B=0，且A=C≠0 B.B=1且D2+E2-4AF＞0
C.B=0且A=C≠0，D2+E2-4AF≥0 D.B=0且A=C≠0,D2+E2-4AF＞0
4.过点P(-8，-1)，Q(5，12)，R(17，4)三点的圆的圆心坐标是( )
A.(
，5) B.(5，1) C.(0，0) D.(5，-1)
5.若两直线y=x+2k与y=2x+k+1的交点P在圆x2+2=4的内部，则k的范围是( )
A.- ＜k＜-1 B.-
＜k＜1
C.- 
＜k＜1 D.-2＜k＜2
二、填空题
6.圆x2+y2+ax=0(a≠0)的圆心坐标和半径分别是 .
7.若方程a2x2+(2a+3)y2+2ax+a+1=0表示圆，则实数a的值等于 .
8.直线y=3x+1与曲线x2+y2=4相交于A、B两点，则AB的中点坐标是 .
三、解答题
9.求圆心在直线2x-y-3=0上，且过点(5，2)和(3，-2)的圆的方程.
10.光线l从点P(1，-1)射出，经过y轴反射后与圆C：(x-4)2+(y-4)2=1相切，试求直线l所在的直线方程.
【素质优化训练】
一、选择题
1.直线
x+y-2=0截圆x2+y2=4得的劣弧所对的圆心角为(全国高考题)( )
A. 
B.
C.
D.
2.对于满足x2+(y-1)2=1的任意x,y，不等式x+y+d≥0恒成立，则实数d的取值范围是( )
A.［-1，+∞］ B.(-∞，-1)
C.［ +1,+∞］ D.(-∞, +1)
3.若实数x，y满足x2+y2=1,则
的最小值等于( )
A. 
B. 
C.
D.2
4.过点P(1，2)的直线l将圆x2+2-4x-5=0分成两个弓形，当大、小两个弓形的面积之差最大时，直线l的方程是( )
A.x=1 B.y=2 C.x-y+1=0 D.x-2y+3=0
5.一辆卡车宽2.7米，要经过一个半径为4.5米的半圆形隧道(双车道，不得违章)，则这辆卡车的平顶车篷篷顶距离地面的高度不得超过( )
A.1.8米 B.3米 C.3.6米 D.4米
二、填空题
6.若实数x,y满足x2+y2-2x+4y=0，则x-2y的最大值是 .
7.若集合A={(x、y)｜y=-｜x｜-2}，B={(x,y)｜(x-a)2+y2=a2}满足A∩B=
，则实数a的取值范围是
.
8.过点M(3，0)作直线l与圆x2+y2=16交于A、B两点，当θ= 时，使△AOB的面积最大，最大值为 (O为原点).
三、解答题
9.令圆x2+y2-4x-6y+12=0外一点P(x,y)向圆引切线，切点为M，有｜PM｜=｜PO｜,求使｜PM｜最小的P点坐标.
10.已知圆C：(x+4)2+y2=4和点A(-2，0)，圆D的圆心在y轴上移动，且恒与圆C外切，设圆D与y轴交于点M、N，求证：∠MAN为定值.
11.已知直角坐标平面内点Q(2，0)，圆C：x2+y2=1，动点M到圆C的切线长与｜MQ｜的比等于常数λ(λ＞0)，求动点M的轨迹方程，并说明轨迹是什么曲线.
12.自点A(-3，3)发出的光线l射到x轴上，被x轴反射，其反射光线m所在直线与圆x2+y2-4x-4y+7=0相切，求光线l与m所在直线方程.
13.AB是圆O的直径，且｜AB｜=2a,M是圆上一动点，作MN⊥AB，垂足为N，在OM上取点P，使｜OP｜=｜MN｜，求点P的轨迹.
参考答案：
【同步达纲练习】
A级
1.B 2.C
3.B 4.D 5.C
6.x=2或3x-4y-2=0 7.-2≤a≤2 8.x+y-3=0，x-y-3=0 9.m=3 10.(
,)
AA级
1.B 2.D
3.D 4.D 5.B
6.(- 
,0), 
7.-1 8.(- 
，
) 9.(x-2)2+(y-1)2=10 10.3x+4y+1=0或4x+3y-1=0
【素质优化训练】
1.C 2.A
3.B 4.D 5.C
6.10 7.-2(+1)＜a＜2(+1) 8.θ=arccot2 或π-arccot2, 8 9.P(
,
) 10.60°
11.M的轨迹方程为(λ2-1)(x2+y2)-4λ2x+(1+4x2)=0，当λ=1时，方程为直线x=
.
当λ≠1时，方程为(x-
)2+y2=
它表示圆，该圆圆心坐标为(,0)半径为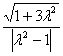
12.l的方程为：3x+4y-3=0或4x+3y+3=0 M的方程为3x-4y-3＝0或4x-3y+3＝0
13.x2+(y±)2=()2轨迹是分别以CO，CD为直径的两个圆.