西安中学2000~2001学年度第一学期期末高二解析几何试题
一、选择题:
1.已知点M(3,4),N(12,7),P在直线MN上,且![]() ,则点P的坐标是( )
,则点P的坐标是( )
A.(6,5) B.(9,6) C.(0,3) D.(0,3)或(6,5)
2.圆![]() 上到直线x+y+1=0的距离等于
上到直线x+y+1=0的距离等于![]() 的点共有( )
的点共有( )
A.一个 B.两个 C.三个 D.四个
3.过点(0,-2)的直线l的倾斜角α满足![]() ,则l的方程是
,则l的方程是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.点(a,b)关于直线x+y=1对称的点的坐标是
A.(1-a,1-b) B.(1-b,1-a) C.(-a-b) D.(-b,-a)
5.直线ax+by-1=0在y轴上的截距是-1,而且它的倾斜角是直线![]() 的倾斜角的两倍,则
的倾斜角的两倍,则
A.![]() ,b=1 B.
,b=1 B.![]() ,b=
,b=![]() ,b=1 D.
,b=1 D.![]() ,b=-1
,b=-1
6.设P是圆![]() 上的点,则P点到直线3x+4y-2=0的最长距离是( )
上的点,则P点到直线3x+4y-2=0的最长距离是( )
A.9 B.
7.椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,CD是过
,CD是过![]() 的弦,则
的弦,则![]() 周长是
周长是
A.10 B.
8.若椭圆![]() 两准线间的距离是焦距的3倍,则它的离心率是( )
两准线间的距离是焦距的3倍,则它的离心率是( )
A.3 B.![]() C.
C.![]() D.
D.![]()
9.已知椭圆![]() 上一点P到它的右准线的距离是10,则P点到它的左焦点的距离是( )
上一点P到它的右准线的距离是10,则P点到它的左焦点的距离是( )
A.14 B.
10.已知集合![]() 与
与![]() 满足M∩N=N,则r的取值范围是
满足M∩N=N,则r的取值范围是
A.![]() B.(0,1) C.
B.(0,1) C.![]() D.(0,2)
D.(0,2)
11.已知点![]() 为椭圆
为椭圆![]() 上的点,
上的点,![]() ,
,![]() 是椭圆的两焦点,点Q在
是椭圆的两焦点,点Q在![]() 上,且
上,且![]() ,那么点Q分有向线段
,那么点Q分有向线段![]() 的比是
的比是
A.3:4 B.4:
12.已知两点P(-2,-2)和Q(0,-1),取一点R(2,m)使PR+RQ最小,则m为
A.![]() B.
B.![]()
二、填空题:
1.平行于直线x-y-2=0。且与它的距离为![]() 的直线方程为_____________。
的直线方程为_____________。
2.经过点A(3,1),B(-7,1),的圆与x轴相交两点的弦长为8,则此圆的方程为________。
3.焦点在x轴上,其长轴端点与相近的焦点相距为1,与相近的一条准线距离为![]() 的椭圆方程__________________。
的椭圆方程__________________。
4.设![]() 是椭圆
是椭圆![]() 的左焦点,P是此椭圆上的动点,A(1,1)是一定点,则
的左焦点,P是此椭圆上的动点,A(1,1)是一定点,则![]() 的最大值是____________________。
的最大值是____________________。
三、解答题:
1.当直线y=kx经过圆![]() 的圆心时,求直线被圆截得的线段长及k的值。
的圆心时,求直线被圆截得的线段长及k的值。
2.已知A(0,0),B(8,0),C(7,6)是△ABC的三个顶点
(1)求它的外心M,垂心H,重心G的坐标
(2)求证:MGH三点共线
3.已知点P(0,1),过P作一直线,使它夹在两已知直线![]() ,和
,和![]() 之间的线段被点P平分,求此直线的方程
之间的线段被点P平分,求此直线的方程
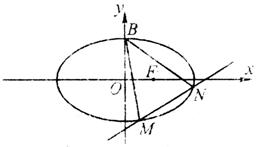
4.已知椭圆的中心在原点,焦点在轴上,直线l:6x-5y-28=0与椭圆交于M,N两点,B为短轴的上端点,且短轴长为整数,若△MBN的重心恰为椭圆的右焦点F。
(1)求此椭圆的方程:
(2)设此椭圆的左焦点为![]() ,问在椭圆上是否存在一点P,使得
,问在椭圆上是否存在一点P,使得![]() ,并证明你的结论。
,并证明你的结论。
2000~2001学年度第一学期期末高二解析几何答案
一、选择题:(每题4分,共48分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | D | B | D | B | C | C | B | C | B | D |
二、填空题:(每空4分,共16分)
1.x-y+4=0 x-y-8=0 2.![]()
3.![]() 4.
4.![]()
三、解答题:(第1题5分,)
1.圆的方程为![]()
∴圆心(1,-2)半径r=1,于是k=-2,直线被圆截得的弦为直径。
∴其长为2。
2.简解:
(1)外心![]() ,垂心
,垂心![]() ,重心G(5,2)
,重心G(5,2)
(2)∵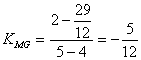 ,
,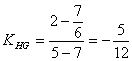
∴M、H、G三点共线。
3.设直线1与![]() ,
,![]() 分别交于A(a,b)和B(m,n)则
分别交于A(a,b)和B(m,n)则
a-3b+10=0,
∴![]() ,
,![]()
由上述四式解得![]() ,即B(4,0)
,即B(4,0)
∴直线l过B(4,0),P(0,1)两点,它的方程是
![]() ,即x+4y-4=0
,即x+4y-4=0
4.(1)设椭圆方程为![]() ,M、N、B的坐标分别为
,M、N、B的坐标分别为![]() 、
、![]() 、B(0,b),则
、B(0,b),则
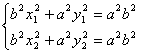 两式相减得,
两式相减得,
![]() ……①
……①
由![]() ,
,![]()
得![]() ,
,![]() 代入①得
代入①得
![]() 或b=
或b=
两点M、N在直线l上得![]()
∴
由②、③得(∵2b∈Z)b=4,c=2,![]()
∴椭圆方程为![]()
(2)先证明![]() ,则∠
,则∠![]()
∴使∠![]() 的点P不存在。
的点P不存在。