高二数学下学期期末考试卷
高二数学试卷(实)
命题人:周湖平 2008、6、20
第I卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在复平面内,复数![]() 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.设集合A={-1, 0, 1},集合B={0, 1, 2, 3},定义A*B={(x, y) x∈A∩B, y∈A∪B},则A*B中元素个数是( )
A.7 B
3、![]() =( )
=( )
A、![]() B、3 C、-1 D、-3
B、3 C、-1 D、-3
4、函数![]() 的图像过点(-1,3),则函数
的图像过点(-1,3),则函数![]() 的图像关于
的图像关于![]() 轴对称的图形一定过点( )
轴对称的图形一定过点( )
A (1,-3) B (-1,3) C (-3,-3) D (-3,3)
5、已知![]() 的图象过点(2,1),则函数
的图象过点(2,1),则函数![]() 的值域为( )
的值域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.在股票买卖过程中,经常用到两种曲线:一种是即时价格曲线![]() (实线表示),另一种是平均价格曲线
(实线表示),另一种是平均价格曲线![]() (虚线表示)(如
(虚线表示)(如![]() 是指开始买卖后三小时的即时价格为10元;
是指开始买卖后三小时的即时价格为10元;![]() 表示三个小时内的平均价格为10元)。下列给出的四个图像中,可能正确的是( )
表示三个小时内的平均价格为10元)。下列给出的四个图像中,可能正确的是( )
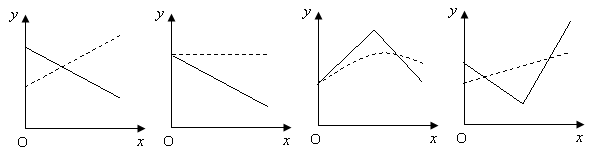
A B C D
7.设方程 ![]() 的两个根为
的两个根为![]() ,则 ( )
,则 ( )
A ![]() B
B
![]() C
C ![]() D
D ![]()
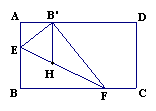 8.有一矩形纸片ABCD,按图所示方法进行任意折叠,使每次折叠后点B都落在边AD上,将B的落点记为
8.有一矩形纸片ABCD,按图所示方法进行任意折叠,使每次折叠后点B都落在边AD上,将B的落点记为![]() ,其中EF为折痕,点F也可落在边CD上,过
,其中EF为折痕,点F也可落在边CD上,过![]() 作
作![]() H∥CD交EF于点H,则点H的轨迹为( )
H∥CD交EF于点H,则点H的轨迹为( )
A.四分之一圆 B.四分之一椭圆
C.双曲线的一部分 D.抛物线的一部分
9.已知实数x满足x<1,n是大于1的整数,记![]() ,则( )
,则( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]() 的大小不定
的大小不定
10.已知f ( x )是定义在实数集R上的不恒为零的函数,且对于任意a、b∈R,满足f (ab)=af ( b )+bf ( a ),f ( 2 )=2,记,,其中n∈N*,考查下列结论:①f ( o )=f ( 1 ) ②f ( x )是R上的偶函数 ③数列{an}为等比数列 ④数列{bn}等差数列,其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
11.有编号分别为1,2,3,4,5的5个红球和5个黑球,从中取出4个,则取出的球的编号互不相同的概率为 ( )
A. ![]() . B.
. B. ![]() . C.
. C. ![]() D.
D. ![]()
12、已知方程![]() 的两实根
的两实根![]() 满足
满足![]() ,
,![]() ,则
,则![]() ( )
( )
A.有最大值但无最小值 B. 有最小值但无最大值
C. 既有最大值也有最小值 D. 既无最大值也无最小值
第II卷(选择题 共90分)
二、填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)
13.已知 ![]() ,且非p是非q的充分条件,则a的取值范围为
,且非p是非q的充分条件,则a的取值范围为
![]() .
.
14.值域为{2,5,10},其对应关系为![]() 的函数的个数
的函数的个数![]() .
.
15.已知![]() 则
则![]() 的最小值是
的最小值是 ![]() .
.
16.给出下列四个命题
①已知函数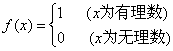 ,则f(x)为偶函数
,则f(x)为偶函数
②函数![]() 与函数
与函数![]() 互为反函数.
互为反函数.
③函数![]() 在
在![]() 处取得极大值
处取得极大值
④已知函数![]() 的图象在M(1,f(1))处的切线方程是
的图象在M(1,f(1))处的切线方程是![]() +2,则
+2,则![]() 3.
3.
其中真命题的代号是:_____________________(写出所有真命题的代号)
三、解答题(本大题共6小题,共74分,解答写出必要的文字说明,注明过程及演算步骤)
17.(本小题满分12分)
已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
18.(本小题满分12分)
 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和
平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,
求他们在同一分数段的概率.
19.(本小题满分12分)
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
设随机变量ξ表示密码中不同数字的个数.
(Ⅰ)求P(ξ=2)
(Ⅱ)求随机变量ξ的分布列和它的数学期望.
20、(本小题满分12分)
|
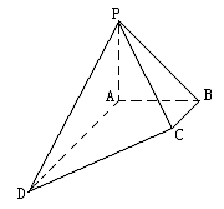
(Ⅰ) 求点D到平面PBC的距离;
(Ⅱ) 求二面角![]() 的大小.
的大小.
21.(本小题满分12分)
(12分)设a为常数,![]() .
.
(1)若![]() 对
对![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
(2)求![]() 有极值的条件及相应的极值.
有极值的条件及相应的极值.
22.(本小题满分14分)
已知函数fn(x)(n∈N*)具有性质:
![]() fn(0)=
fn(0)=![]() ,
,
n[fn(![]() )-fn(
)-fn(![]() )]=[fn(
)]=[fn(![]() )-1]fn(
)-1]fn(![]() ),k=(0,1,2,…,n-1).
),k=(0,1,2,…,n-1).
(1)当n为一定值时,记ak=![]() ,求ak的表达式(k=0,1,2,…,n);
,求ak的表达式(k=0,1,2,…,n);
(2)对n∈N*,证明:![]() <fn(1)≤
<fn(1)≤![]()
参考答案
一、选择题:(本题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | A | B | C | C | D | D | A | C | D | A |
二、填空题(本题共4小题,每小题4分,共16分)
13.![]() 14.27 15.
14.27 15.![]() 16.① ③_
16.① ③_
三、解答题
17.解:由![]() ,得:
,得:![]() ,
,
![]()
![]() ,
,![]()
![]() .
.![]()
当![]() 时,原不等式的解集
时,原不等式的解集![]() 不是
不是![]() 的子集.
的子集. ![]()
当![]() 时,∵
时,∵![]() ,
,
![]()
(1)当![]() 时,
时,![]() ,则
,则![]() ,此时,不等式的解集
,此时,不等式的解集![]() ;
;![]()
(2)当![]() 时,
时,![]() ,故
,故![]() ;
;![]()
(3)当![]() 时,
时,![]() ,则
,则![]() ,此时,不等式的解集
,此时,不等式的解集![]() 不是
不是![]() 的子集;
的子集; ![]()
(4)当![]() 时,
时,![]() ,此时,不等式的解集
,此时,不等式的解集![]() 不是
不是![]() 的子集.综上,
的子集.综上,![]() .
.
![]()
18.解:(Ⅰ)因为各组的频率和等于1,故第四组的频率:![]() ……2分
……2分
直方图如右所示……………………………….4分
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 ![]()
所以,抽样学生成绩的合格率是![]() %......................................6分
%......................................6分
利用组中值估算抽样学生的平均分
![]() ………………….8分
………………….8分
=![]() =71
=71
估计这次考试的平均分是71分………………………………………….9分
(Ⅲ)![]() ,
,![]() ,
,![]() ”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
![]()
![]() …………12分
…………12分
19.解:(Ⅰ)密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.
![]() …………………………………………………………………4分
…………………………………………………………………4分
(Ⅱ)由题意可知,ξ的取值为2,3,4三种情形.
若ξ= 3,注意表格的第一排总含有数字1,第二排总含有数字2则密码中只可能取数字1,2,3或1,2,4.
![]() 若
若![]()
(或用![]() 求得). ………………………………………………8分
求得). ………………………………………………8分
![]() 的分布列为:
的分布列为:
| ξ | 2 | 3 | 4 |
| p |
|
|
|
![]() ……………………………………………12分
……………………………………………12分
20.解:解法一
((Ⅰ)如图,在四棱锥![]() 中,
中,
∵BC∥AD,从而点D到平面PBC间的距离等于点A到平面PBC的距离.
∵∠ABC=![]() ,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,∴BC⊥平面 PAB,………2分
,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,∴BC⊥平面 PAB,………2分
∴平面PAB⊥平面PBC,交线为PB,过A作AE⊥PB,垂足为E,则AE⊥平面PBC,
|
即点D到平面PBC的距离为![]() .………………6分
.………………6分
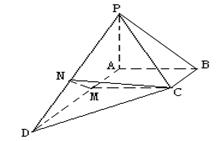
(Ⅱ) ∵PA⊥底面ABCD,∴平面PAD⊥底面ABCD,
引CM⊥AD于M,MN⊥PD于N,则CM⊥平面PAD,
∴MN是CN在平面PAD上的射影,由三垂线定理可知CN⊥PD,
∴∠CNM是二面角![]() 的平面角.…………9分
的平面角.…………9分
依题意![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
可知![]() ,∴
,∴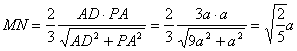 ,
,
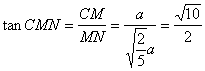 ,∴二面角
,∴二面角![]() 的大小为
的大小为![]() …… 12分
…… 12分
解法二:如图, A为原点,分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系.
|
∴![]() ,
,
∴![]() . 则
. 则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面PBC的一个法向量为![]() ,则
,则
![]() 令
令![]() ,得
,得![]() ,
,
则点D到平面PBC的距离等于
![]() .……………6分
.……………6分
(Ⅱ) ∵AB⊥PA,AB⊥AD,∴AB⊥底面PDA,∴平面PDA的一个法向量为![]() .
.
设平面PDC的一个法向量为![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() 令
令![]() ,得
,得![]() ,∴
,∴![]() .
.
∵二面角![]() 是锐二面角,∴二面角
是锐二面角,∴二面角![]() 的大小为
的大小为![]() .……12分
.……12分
21.解.(1)易得![]() ,故原条件化为
,故原条件化为![]() 对
对![]() 恒成立.令
恒成立.令![]() ,则
,则![]() ,当
,当![]() 时显然有
时显然有![]() ,故
,故![]() 上单调递增,从而
上单调递增,从而![]() .故所求a的取值范围是
.故所求a的取值范围是![]() …………6分
…………6分
(2)![]() .
.
①若![]() ,则
,则![]() 时
时![]() ,即
,即![]() 在
在![]() 单减;
单减;![]() 时,
时,![]() ,即
,即![]() 在
在![]() 单增,从而
单增,从而![]() 有极小值
有极小值![]() -2a
-2a
②若![]() ,则
,则![]() 时
时![]() ,即
,即![]() 在其定义域上是增函数,从而无极值.
在其定义域上是增函数,从而无极值.
综上所述,当且仅当![]() 时
时![]() 有极小值
有极小值![]() .………………12分
.………………12分
22.解: (1)因为n[fn(![]() )-fn(
)-fn(![]() )]=[fn(
)]=[fn(![]() )-1]·fn(
)-1]·fn(![]() ),所以
),所以![]() -
-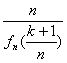 =1, ………2分
=1, ………2分
即(n+1)ak-nak+1=1. ………………3分 所以![]() =1+
=1+![]() .………………5分
.………………5分
因为n为定值,所以数列{ak-1}是以a0-1为首项,1+![]() 为公比的等比数列,可得ak=1+(1+
为公比的等比数列,可得ak=1+(1+![]() )k(k=0,1,2,…,n). ………………6分
)k(k=0,1,2,…,n). ………………6分
(2)证明:因为ak=![]() ,所以fn(1)=
,所以fn(1)=![]() =
=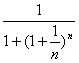 ).要证
).要证![]() <f(1)≤
<f(1)≤![]() ,只需证2≤(1+
,只需证2≤(1+![]() )n<3. ………………8分
)n<3. ………………8分
因为(1+![]() )n=1+C
)n=1+C![]()
![]() +C
+C![]()
![]() +…+C
+…+C![]()
![]() =1+1+…≥2. ………………10分
=1+1+…≥2. ………………10分
又(1+![]() )n=1+C
)n=1+C![]()
![]() +C
+C![]()
![]() +…+C
+…+C![]()
![]() =1+1+
=1+1+![]() +…+
+…+![]() ≤1+1+
≤1+1+![]() +
+![]() +…+
+…+![]() <1+1+
<1+1+![]() +
+![]() +…+
+…+![]() =3-(
=3-(![]() )n<3, 所以原命题成立. ………………14分
)n<3, 所以原命题成立. ………………14分