高二数学下学期期末联考试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试用时120分钟．祝各位同学考试顺利！
第Ⅰ卷
一、选择题：每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若
，则“
”是“
”的（ ）．
（A）必要非充分条件； （B）充分非必要条件；
（C）充要条件； （D）既不充分也不必要条件．
2．经过点（0，0），且与以（2，－1）为方向向量的直线垂直的直线方程为（ ）．
（A）
；
（B）
；
（C）
；
（D）
．
3．已知动点P（
，
）满足
，则点P的轨迹是（ ）．
（A）椭圆； （B）双曲线； （C）抛物线； （D）两相交直线．
4．（文科）给出以下四个命题：
①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行；
②如果一条直线和一个平面内的两条直线都垂直，那么这条直线垂直于这个平面；
③如果两条直线都平行于一个平面，那么这两条直线互相平行；
④如果两条直线同垂直一个平面，那么这两条直线平行．
其中真命题的个数是（ ）．
（A）4； （B）3； （C）2； （D）1．
（理科）对于任意的直线
与平面
，在平面内必有直线
，使与（ ）．
（A）平行； （B）相交； （C）垂直； （D）互为异面直线．
5．若关于的不等式
的解集为
，则实数
的取值范围为（ ）．
（A）
； （B）
； （C）
； （D）
．
6．已知直线：
与以A（1，4）、B（3，1）为端点的线段相交，则实数的取值范围是（ ）．
（A）
； （B）
； （C）
； （D）或．
7．已知圆C：
及直线：
．当直线被圆C截得的弦长为
时，则
（ ）．
（A）
； （B）
； （C）
； （D）
．
8．已知点A（3，2），F为抛物线
的焦点，点P在抛物线上移动，当
取得最小值时，点P的坐标是（ ）．
（A）（0，0）； （B）（2，2）； （C）（－2，－2） （D）（2，0）．
9．（文科）已知
，
，
，则
的最小值是（ ）．
（A）
；
（B）
； （C） 
；
（D）5．
（理科）已知
，则
有（ ）．
（A）最大值
； （B）最小值； （C）最大值1； （D）最小值1．
10．点P是双曲线
上的一点，
和
分别是双曲线的左、右焦点，
，则
的面积是（ ）．
（A）24； （B）16； （C）8； （D）12．
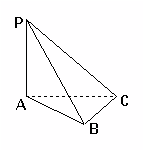11．如图1，PA⊥平面ABC，∠ACB＝
，且PA ＝AC＝BC＝，则异面直线PB与AC所成的角是（ ）．
（A）
； （B）
；
（C）
； （D）
．
图1
12．（文科）已知椭圆
的左，右焦点分别为、，点P在椭圆上，且
，则此椭圆的离心率的最小值为（ ）．
（A）
； （B）
； （C）
； （D）
．
（理科）已知E、F是椭圆
的左、右焦点，是椭圆的一条准线，点P在上，则∠EPF的最大值是（ ）．
（A）
； （B）
； （C）
； （D）
．
第Ⅱ卷
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13．，
是空间两条不同直线，
是两个不同平面，下面有四个命题：
①若
，
，
，则
；
②若，，，则；
③若，，
，则
；
④若，
，，则．
其中真命题的编号是 ．（写出所有真命题的编号）
14．对于圆
上任一点
，不等式
恒成立，则实数的取值范围
．
15．设
满足约束条件：
则目标函数
的最大值是
．
16．已知抛物线
的对称轴为
，焦点为（1，1），则此抛物线的准线方程是
．
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（12分）设，解关于的不等式：
．
18．（12分）过抛物线
的焦点的一条直线和此抛物线相交于两个点A、B，经过点A和抛物线顶点的直线交准线于点M．
求证：（Ⅰ）
；
（Ⅱ）直线MB平行于抛物线的对称轴．
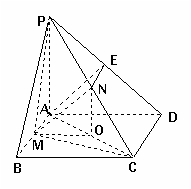
19．（12分）如图2，已知四边形ABCD为矩
形，PA⊥平面ABCD，M、N分别为AB、PC的中点．
（Ⅰ）求证：MN⊥CD．
（Ⅱ）在棱PD上是否存在一点E，使得 图2
AE∥平面PMC？若存在，请确定点E的位置；若不存在，请说明理由．
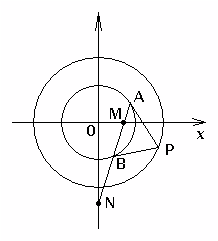20．（12分）如图3，过圆
上的动
点P向圆
（
）引两条切线
PA、PB，切点分别为A、B，直线AB与轴、
轴分别交于M、N两点，求△MON面积的最小值．
21．（12分）已知
，
，
求证：
．
22．（14分）文科做（Ⅰ）、（Ⅱ）；理科做（Ⅰ）、（Ⅲ）． 图3
已知点B（2，0），
，O为坐标原点，动点P满足
．
（Ⅰ）求点P的轨迹
的方程；
（Ⅱ）当为何值时，直线：
与轨迹相交于不同的两点M、N，且满足
？
（Ⅲ）是否存在直线：
与轨迹相交于不同的两点M、N，且满足？若存在，求出的取值范围；若不存在，请说明理由．
答案与提示:
一、选择题
1—5 BDBCB； 6—12 BCBBD BB．
提示：
1．由
；
反之由
不能推得
．
故“”是“”的充分非必要条件．选（B）．
2．由题设知已知直线的斜率为
，∴所求直线的斜率为2；
又所求直线过原点，故为所求．选（D）．
3．由题设知动点P到定点（1，0）的距离和它到定直线
的距离的比是常数，根据双曲线的第二定义可得点P的轨迹为双曲线．选（B）．
4．（文科）①、④正确，选（C）．
（理科）对于任意的直线与平面，若在平面内，则存在直线m⊥；
若不在平面内，且⊥，则平面内任意一条直线都垂直于；
若不在平面内，且与不垂直，则它的射影在平面内为一条直线，在平面内必有直线垂直于它的射影，则⊥．故选（C）．
5．由
知
．选（B）．
6．由A（1，4）、B（3，1）在直线上或其异侧得
．
解得．选（B）．
7．设截得的弦为AB，圆心为
，作
于H，则由平几知识得
．
由此得
，解得
．选（C）．
8．点A在抛物线含焦点区域，过A作AP垂直于抛物线的准线交抛物线于点P，则由抛物线的定义知点P（2，2）为所求点．选（B）．
9．（文科）
，选（B）．
（理科）令
，则
．
在
上是单调递增函数，故的最小值是
．选（B）．
10．由得
，
．
∴
＝12．选（D）．
11．如图，过B作BD∥CA，且满足BD＝CA，
则∠PBD为PB与AC所成的角．
易得四边形ADBC为正方形，
由PA⊥平面ABC得BD
PD．
在Rt△PDB中，
，
，
．选（B）．
12．（文科）由题设和焦半径公式得
．
．∴
．即
．选（B）．
（理科）不妨设右准线交轴于点A，由平几知识知过E、F的圆且与相切于点P时，∠EPF最大．由圆幂定理得
．
易得∠FPA＝，∠EPA＝，从而∠EPF＝为所求最大值，故选（B）．
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13．①、④； 14．
）； 15．
； 16．
．
提示：13．②、③为假命题；①、④为真命题．
14．设点
，由题设得
．
即
恒成立．而
，
∴
．故的取值范围为）．
15．如图，作出不等式表示的可行域（阴影部分）
和直线：，将向右上方平行移动，使其经过可
行域内的点Ａ
时，取得最大值．
故当
，
时，
．
16．对称轴与抛物线的交点（0，0）为抛物线的顶点，且抛物线的准线垂直于对称轴，焦点（1，1）关于顶点（0，0）的对称点（－1，－1）在准线上，故所求准线方程为．
三、解答题
17．不等式整理得 
．
当
时，不等式为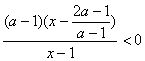 
．……………（3分）
①当
时，
，原不等式解集为
；……………（6分）
②当
时，不等式解集为
；……………（9分）
③当
时，
，原不等式解集为
．……………（12分）
18．（Ⅰ）AB方程为
，代入抛物线方程得
．……………（3分）
由韦达定理得．……………（5分）
（Ⅱ）OA方程为
，与准线方程联立解得M
．………（8分）
∴
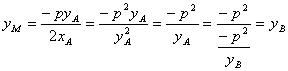．……………（11分）
故直线MB平行于抛物线的对称轴．……………（12分）
19．（Ⅰ）取AC的中点O，连结NO，MO，
由N为PC的中点得NO∥PA．……………（2分）
又PA⊥平面ABCD，∴NO⊥平面ABCD．……………（4分）
又∵OM⊥AB，由三垂线定理得AB⊥MN．
又∵CD∥AB，∴MN⊥CD．……………（6分）
（Ⅱ）存在点E，使得AE∥平面PMC．
此时点E为PD的中点．……………（8分）
证明如下：取PD的中点E，连结NE，
由N是PC的中点得NE∥CD，
．
又 MA ∥CD，
，
∴MA∥NE，MA＝NE．
由此可知四边形MNEA是平行四边形，
∴AE∥MN．
由
平面PMC，
平面PMC，
∴AE∥平面PMC．……………（12分）
20．设
为圆上任一点，则
，
．
由题设知O、A、P、B在以OP为直径的圆上，该方程为
．……………（4分）
而AB是圆和以OP为直径的圆的公共弦，将这两圆方程相减得
直线AB的方程为
．
∴
，
．……………（8分）
．
故△MON面积的最小值为
．……………（12分）
21．∵
，……（3分）
∵，∴
，
即
．……………（6分）
∴
，……………（11分）
故．……………（12分）
22．（Ⅰ）设点
，则
，
．
由题设得
．………（3分）
即点P到两定点（0，）、（0，－）的距离之和为定值
，故轨迹是以（0，
）为焦点，长轴长为的椭圆，其方程为
．……（6分）
（Ⅱ）设点M 
、N
，线段MN的中点为
，
由得
垂直平分
．
联立
消去得
．
由
得
．………（10分）
∴
，
．即
．
由⊥得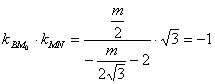
．
故
为所求．………（14分）
（Ⅲ）若存在直线与椭圆相交于不同的两点M 、N，且满足
，令线段MN的中点为，则垂直平分．
联立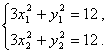
两式相减得
．
∴
．
又由⊥得
．∴
，
．
即
．………（10分）
又点
在椭圆的内部，故
．即
．
解得
.又点在直线上，∴
．
∴
（当且仅当
时取等号）．
故存在直线满足题设条件，此时的取值范围为
．………（14分）