高二数学下期期末考试试题
高2009级数学试题(理科)
考试时间120分钟 满分150分
命题人:魏华 审题人:邱旭
一、选择题:本大题共12小题,每题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的答案填在后面的括号内
1.某研究所有编号为1,2,3,4的四个饲养房,分别饲养有18、54、24、48只白鼠供试验用,某项试验需抽取24只白鼠,你认为最合适的抽样方法为( )
(A)在每个饲养房各抽取6只
(B)为所有白鼠都加上编有不同号码的项圈,用随机抽样法确定24只
(C)在四个饲养房分别抽取3、9、4、8只
(D)先确定这四个饲养房应分别抽出3、9、4、8只样品,再由各饲养房自己加号码项圈,用简单随机抽样确定各自抽出的对象
2.要从四个学校中选出6人作“市优干”,每校至少一名,这6个名额有( )种分配方法.
(A)15 (B)20 (C)10 (D)6
3.3名男生2名女生排成一排,女生甲始终排在女生乙的左边的排法种数是( )
(A)120 (B)60 (C)48 (D)24
4.![]() 的展开式中,常数项为15,则
的展开式中,常数项为15,则![]() 等于( )
等于( )
(A)3 (B)4 (C)5 (D)6
5.将编号为1,2,3,4,5,6的六个小球排成一列,要求1号球与2号球必须相邻,5号球与6号球不相邻,则不同的排法种数有( )
(A)36 (B)142 (C)48 (D)144
6.![]() 的值为( )
的值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.在大小等于![]() 的二面角
的二面角![]() 内,放一半径为3的球O,球O与半平面
内,放一半径为3的球O,球O与半平面![]() 分别切于A、B两点,则过A、B两点的球面距离等于( )
分别切于A、B两点,则过A、B两点的球面距离等于( )
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.在正方体![]() 中,P是侧面
中,P是侧面![]() 内
内
一动点,若P到直线BC与到直线![]() 的距离相等,则动
的距离相等,则动
点P的轨迹所在曲线是( )
(A)直线 (B)圆
(C)双曲线 (D)抛物线
9.一个四面体共一个顶点的三条棱两两互相垂直,其长分别为![]() ,且四面体的四个顶点在同一个球面上,则这个球的表面积为( )
,且四面体的四个顶点在同一个球面上,则这个球的表面积为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.从正方体的六个面中选取3个面,其中2个面不相邻的概率是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.已知![]() ,则
,则![]() ( )
( )
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
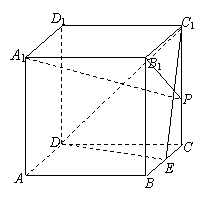
12.在棱长为4的正方体![]() 中,
中,
点E、F分别在棱![]() 和
和![]() 上,且
上,且![]() ,
,
则![]() 的最大值为( )
的最大值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
高二数学下期期末考试试题
高2009级数学答卷
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:本大题共4小题,每题4分,共16分,把答案填在题中的横线上
13.设随机变量![]() 的分布列为:
的分布列为:
|
| 0 | 1 | 2 |
|
|
|
|
|
则![]() 的数学期望
的数学期望![]() 的最大值为
.
的最大值为
.
14.在![]() 的展开式中,系数最小的项是
.
的展开式中,系数最小的项是
.
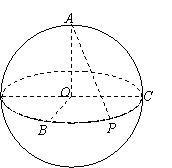
15.如图,A、B、C是球O的球面上三点,且OA、OB、OC
两两垂直,P是球O的大圆上BC弧上的中点,则直线AP与OB
所成角的弧度数是 .
16.已知![]() ,若
,若![]() 为满足
为满足![]() 的一随机整数,则
的一随机整数,则![]() 是
是![]() 的概率是_____________.
的概率是_____________.
三、解答题:本大题共6小题,共74分
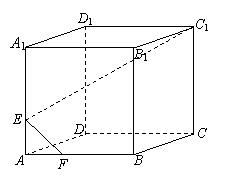
17.(12分)在长方体![]() 中,
中,![]() ,
,![]() 分
分![]() 所成比为2,
所成比为2,
 (1)求点
(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
18.(12分)甲、乙两人参加一次英语口语考试,已知在编号为1~10的10道试题中,甲能答对编号为1~6的6道题,乙能答对编号为3~10的8道题,规定每位考生都从备选题中抽出3道试题进行测试,至少答对2道才算合格,
(1)求甲答对试题数![]() 的概率分布及数学期望;
的概率分布及数学期望;
(2)求甲、乙两人至少有一人考试合格的概率.
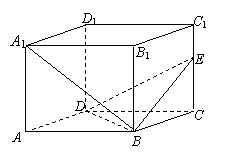
 19.(12分)如图所示的正方体
19.(12分)如图所示的正方体![]() 中,E是BC的中点,在
中,E是BC的中点,在![]() 上求一点P,使面
上求一点P,使面![]() 面
面![]() .
.
20.(12分)如图,直四棱柱![]() 的高为3,底面是边长为4的菱形 ,且
的高为3,底面是边长为4的菱形 ,且![]() ,
,![]() ,
,
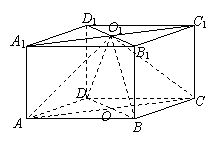 (1)求证:平面
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
21.(12分)一种信号灯,只有符号“√”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“√”和“×”两者之一,其中出现“√”的概率为![]() ,出现“×”的概率为
,出现“×”的概率为![]() ,若第
,若第![]() 次出现“√”,记为
次出现“√”,记为![]() ,若第
,若第![]() 次出现“×”,则记为
次出现“×”,则记为![]() ,令
,令![]() ,
,
(1)求![]() 的概率;
的概率;
(2)求![]() ,且
,且![]() 的概率.
的概率.
22.(14分)设![]() ,试比较
,试比较![]() 与
与![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
高二期末测试题(理科)参考答案
一、选择题(每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选项 | D | C | B | D | D | D | A | D | A | B | C | B |
二、填空题(每题4分,共16分)
13、![]() ;
14、
;
14、![]() ; 15、
; 15、![]() ; 16、
; 16、![]()
 三、解答题(共74分)
三、解答题(共74分)
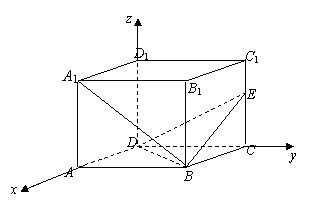
17、解:(1)如图建立空间直角坐标系:
![]() 。(3分)
。(3分)
设面![]() 的法向量为
的法向量为![]() ,
,
所以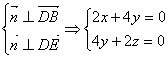 ,
,
令![]() ,则
,则![]() 。
(6分)
。
(6分)
 。
(8分)
。
(8分)
(2)![]() (9分)
(9分)
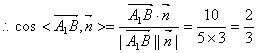 。
(11分)
。
(11分)
所以直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() 。
(12分)
。
(12分)
18、解:(1)![]() ;
(1分)
;
(1分)
![]() ;
(2分)
;
(2分)
![]() ;
(3分)
;
(3分)
![]() 。
(4分)
。
(4分)
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
所以![]() 的分布列为
(5分)
的分布列为
(5分)
![]() 。
(6分)
。
(6分)
(2)![]() (甲合格)=
(甲合格)=![]() ;
(8分)
;
(8分)
![]() (乙合格)=
(乙合格)=![]() ;
(10分)
;
(10分)
所求![]() =
=![]() 。
(12分)
。
(12分)
19、解:以D为原点,DA为![]() 轴,DC为
轴,DC为![]() 轴,DD1为
轴,DD1为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
设正方体棱长为2,且![]() ,则
,则
![]() ,
,![]() ,
,
设![]() 且
且![]() 平面
平面![]() ,则
,则
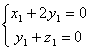 ,取
,取![]() 。
(4分)
。
(4分)
又![]() ,
,![]() ,
,
设![]() 且
且![]() 平面
平面![]() ,则
,则
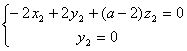 ,取
,取![]() 。
(8分)
。
(8分)
由面![]() ⊥面
⊥面![]() ,得
,得![]()
即![]() 解得
解得![]() 。
。
故![]() 为
为![]() 的中点。
(12分)
的中点。
(12分)
(注:几何证法:由EC1⊥A1B1,在面BCC1B1内,过B1作B1P⊥EC1交CC1于P,易知P为CC1中点。酌情给分)
20、解:(1)![]() 是直四棱柱,
是直四棱柱,
![]() 面
面![]() ,又
,又![]() 面
面![]() ,所以
,所以![]() 。
(2分)
。
(2分)
又![]() 是菱形,
是菱形,![]()
所以![]() 面
面![]() 。
(4分)
。
(4分)
即![]() 面
面![]() ,又
,又![]() 面
面![]() ,
,
所以平面![]() 平面
平面![]() 。
(6分)
。
(6分)
(2)过O作![]() 于H,连接
于H,连接![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角。 (8分)
的平面角。 (8分)
在![]() 中,
中,![]() 。
(10分)
。
(10分)
又![]() 。
。
![]() 。
。
故二面角![]() 的大小为
的大小为![]() 。
(12分)
。
(12分)
(注:向量解法,酌情给分)
21、解:(1)![]() 即前四次中有三次出现“√”,一次出现“×”,
即前四次中有三次出现“√”,一次出现“×”,
所以概率为![]() 。
(4分)
。
(4分)
(2)![]() ,
(7分)
,
(7分)
![]() ,
(10分)
,
(10分)
所以所求概率为![]() 。
(12分)
。
(12分)
22、证明:![]() ,
,![]() (2分)
(2分)
比较![]() 与
与![]() 的大小,即比较
的大小,即比较![]() 与
与![]() 的大小。 (3分)
的大小。 (3分)
猜想:![]() (当且仅当
(当且仅当![]() 时,等号成立)
(5分)
时,等号成立)
(5分)
下面用数学归纳法加以证明:
(1)当![]() 时,易证。(略)
(7分)
时,易证。(略)
(7分)
(2)假设当![]() 时,猜想成立,即
时,猜想成立,即![]() (8分)
(8分)
当![]() 时,
时,![]() (注:
(注:![]() )
)
要证猜想成立,只需证明![]() (11分)
(11分)
即证![]() 亦即
亦即![]()
由![]() 易得上式成立,即
易得上式成立,即![]() 时,猜想成立。
(13分)
时,猜想成立。
(13分)
综上(1)(2)可知,猜想成立。 (14分)
(另证:令![]() ,要证
,要证![]() ,即证
,即证![]() ,由二项式定理展开,易得证。酌情给分)
,由二项式定理展开,易得证。酌情给分)