高二数学不等式单元测试

高二数学不等式单元测试（不等式⑵）

班级　　　　 学号　　　 　 姓名　　　　　

一、选择题(本大题共12小题，每小题4分，共48分)

1.已知a、b、c∈R,则下面推理中正确的是　　　　　　　　  　　　　　　　　　　 (　　　　 )

A.a＞bam²＞bm²B.＞a＞b　　C.a³＞b³,ab＞0＜ D.a²＞b²,ab＞0＜

2.设x+3y－2=0，则函数z=3^x+27^y+3的最小值是　　　　　　　 　　　　　　　　　　(　　　　 )

A.3　　　　　　　　　　  B.3+2　　　　　　　　　 C.6　　　　　　　　　　 　　　　　  D.9

3.若a＞b＞1,P=,Q=(lga+lgb),R=lg(),则　　 　　　　　　　　　　　(　　　　 )

A.R＜P＜Q　　　　　　　　　　B.P＜Q＜R　　　　　　　 　C.Q＜P＜R　　　　　　　 　D.P＜R＜Q

4. 若log_x(2x²+1)＜log_x(3x)＜0成立，则x的取值范围是　　　　　　　　　　　　 　(　　　　 )

A.(0，)　　　　　　 　　　　B.(0，)　　　　　　 C.(，1)　　　　　 　　　D.(，)

5. 若a、b都是正数，则关于x的不等式－b＜＜a的解集是　　　　　　　  　　 (　　　　 )

A.(－,0)∪(0,)　　　　　　　B.(－,0)∪(0,)　　 C.(－∞,－)∪(,+∞)　　　 D.(－,)

6. 已知h＞0，设甲:两实数a、b满足a－b＜2h；乙:两实数a、b满足a－1＜h且b－1＜h,则(　　　　 )

A.甲是乙的充分但不必要条件　　　　　　　　　  B.甲是乙的必要但不充分条件

C.甲是乙的充要条件　　　　　　  　　　　　　　D.甲既不是乙的充分条件，也不是乙的必要条件

7.若满足x－2＜a的x都适合不等式x²－4＜1，则正数a的取值范围是　　　 　　　　(　　　　 )

A.(0，－2］　　　 　　　B.(－2，+∞)　　　C.［－2,+∞)　　　 D.(－2,+2)

8.当x∈［－1,3］时，不等式a≥x²－2x－1恒成立，则a的最大值和最小值分别为　　 (　　　　 )

A.2，－1　　　　　　　　　　 B.不存在，2　　　 C.2，不存在　　　　　　　　　D.－2，不存在

9. 若关于x的不等式(a²－1)x²－(a－1)x－1＜0对于x∈R成立，则实数a的取值范围是 (　　　　 )

A.(－，1］ 　　　B.［－，1］　　　　　C.(－，1)　　　　　　　 D.(－∞,－)∪［1,+∞)

10.设关于x的不等式恒成立,则a的取值范围是　　　　　  　　 (　　　　 )

A.　　  B.　　　　　  　 C.　　　　　　 D.

11. ，下列不等式一定成立的是　　　　　　　　　　　　　　　　　　　  （　　　　 ）

（A）；（B）；

（C）；

（D）.

12.已知函数,为方程的两根,且,给出下列不等式,其中成立的是　　　　　　　　　　　　　　 　　　　　　　　　　　　 (　　　　 )

①　　　 ②　　  ③　　　　④

A.①④　　　　　 B.③④　　　　　　　　 C.①②　　　　　　　 D.②④

选择题答题卡

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题(本大题共5小题，每小题4分，共20分)

13.若正数a、b满足ab=a+b+3，则ab的取值范围是__________.

14.已知两个正实数x、y满足x+y=4,则使不等式+≥m恒成立的实数m的取值范围是__________.

15.已知三个不等式:①ab＞0；②－＜－；③bcad.以其中两个作为条件，余下一个作为结论，可以组成__________个正确的命题.

16.在下列各命题中:

①a+b－a－b≤2b；　　 ②a、b∈R⁺,且x≠0,则ax+≥2；

③若x－y<ε,则x<y+ε；④当且仅当ab<0或ab=0时,a－b≤a+b中的等号成立.

其中真命题的序号为__________.

  　17. 三个同学对问题“关于的不等式＋25＋－5≥在[1，12]上恒成立，求实数的取值范围”提出各自的解题思路．

甲说：“只须不等式左边的最小值不小于右边的最大值”．

乙说：“把不等式变形为左边含变量的函数，右边仅含常数，求函数的最值”．

丙说：“把不等式两边看成关于的函数，作出函数图像”．

参考上述解题思路，你认为他们所讨论的问题的正确结论，即的取值范围是 　　　　 ．

三、解答题(本大题共5小题，共32分)

18.实数a、b、c、d满足下列三个条件:

①d>c；②a+b=c+d；③a+d<b+c.

请将a、b、c、d按照从大到小的次序排列,并证明你的结论.

19.若,解关于x的不等式.

20.已知函数f(x)=,g(x)=x²－3ax+2a²(a＜0)，若不存在实数x使得f(x)＞1和g(x)＜0同时成立，试求a的范围.

21.已知,求的最小值.

22.设实数适合且，求证：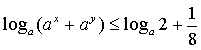

蓬安中学高2009级数学单元测试（不等式⑵）答案

一.选择题

CDBDCB　ABAAAB

解析：1. A中若m=0不成立.B中若c＜0不成立. C中a³－b³＞0(a－b)(a²+ab+b²)＞0∵a²+ab+b²=(a+)²+b²＞0恒成立，故a－b＞0.∴a＞b.又∵ab＞0,∴＜.D中a²＞b²(a+b)(a－b)＞0，不能说明a＞b.故选C.

2. ∵3^x＞0,27^y＞0,∴z=3^x+27^y+3≥2+3=2+3=2+3=9(仅当3^x=27^y，即x=3y时取“=”).

3. a＞b＞1lga＞0,lgb＞0.

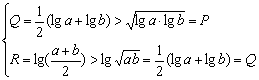
R＞Q＞P.

4. 对于log_x(3x)＜0，若x＞1,则3x＜1,矛盾，故0＜x＜1.又2x²+1＞3x＞1,∴＜x＜.

5. －b＜＜a－b＜＜0或0＜x＜ax＜－或x＞.

6. a－b=(a－1)－(b－1)≤a－1+b－1＜2h.故应选B.

7. x－2＜a的解是2－a＜x＜2+a,x²－4＜1的解是－＜x＜－或＜x＜.由题意得或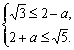由于a是正数，前一不等式组无解，后一不等式组的解是0＜a≤－2.答案:A

8. 分离参数法求参数的最值，转化求函数的最大值.设f(x)=x²－2x－1=(x－1)²－2.当x∈［－1,3］时，f(x)最大值为2，故a≥2.故选B.

9. 当a²－1≠0时，需a²－1＜0且Δ＜0；当a²－1=0,即a=±1时，代入验证.答案:A

10.恒成立, 恒成立,.

11.且

故：B 不一定成立；C 应相等； D 应 “”.

12.设由已知是的两根,得

即；

..

二.填空题：

13. :ab=a+b+3≥2+3，即ab－2－3≥0.解得≥3或≤－1(舍去).∴ab≥9(当且仅当a=b=3时，取等号).答案:［9,+∞)

14. ∵(x+y)·(+)=5++≥9,又∵x+y=4，∴(+)_min=.∴m≤,即(－∞,］.答案:(－∞,］

15. 由②，＞0,又ab＞0bc－ad＞0，即bc＞ad，说明由①②③.同理可证明其他情况.答案:0

16. :∵a+b－a－b≤(a+b)－(a－b)=2b=2b,∴①是真命题.

∵a、b∈R⁺,x≠0,∴ax与同号.∴ax+=ax+≥2=2.∴②是真命题.

∵x－y<ε,∴x－y≤x－y<ε.∴x－y<ε.移项得x<y+ε,∴③是真命题.

当a=－1,b=2时,有ab<0. a－b=1－2=－1,a+b=－1+2=1,则此时a－b≠a+b.∴④是假命题.

∴真命题的序号为①②③.答案:①②③

17.由＋25＋－5≥，而，等号当且仅当时成立；且，等号当且仅当时成立；所以，，等号当且仅当时成立；故；

三.解答题：18.

　　　 由①得b>d>c>a.

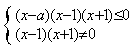
19.解：由当时,解集为；当时,解集为；当时,解集为.

20. 解:由f(x)＞1，得＞1,化简整理得＜0.解得－2＜x＜－1或2＜x＜3.

即f(x)＞1的解集为A={x－2＜x＜－1或2＜x＜3}.

由g(x)＜0得x²－3ax+2a²＜0,即(x－a)(x－2a)＜0(a＜0).则g(x)＜0的解集为B={x2a＜x＜a,a＜0}.

根据题意，有A∩B=.

因此，a≤－2或－1≤2a＜0.

故a的范围是{aa≤－2或－≤a＜0}.

21.解：由a>b>0知a-b>0,

当且仅当都成立时,即当时, 取得最小值16.

22.证明：

.

第一个等号成立的条件：；第二个等号成立的条件：,所以证明的不等式等号不成立