高二数学学生学业水平测试模拟试题（一）
数 学
1．考试采用书面答卷闭卷方式，考试时间90分钟，满分100分。
2．本试卷分第I卷（选择题）和第II卷（非选择题）两部分。其中，第I卷（选择题）的答案须填在第I卷后的答题卡上。
第I卷（选择题 共45分）
一选择题（本大题共18小题，每小题3分，共54分。每小题的四个选项中，只有一个选项符合题目要求。请将正确答案填在第I卷后的答题卡上。）
1：已知
则有
A．
B. 
C.
D. 
2.在三角形ABC中,
,则三角形ABC的形状是
Ａ．直角三角形 Ｂ．锐角三角形
Ｃ．钝角三角形 Ｄ．正三角形
３．已知函数
的定义域为
，
的值域为
，则
Ａ．
Ｂ． 
Ｃ ．（－２，２） Ｄ．
４．下面程序输出的结果为
A． 9， 4
B. 4, 5
C. 9, －1
D. －1, 9
5.有一种波,其波形为函数
的图像,若其在区间[0,t]上至少有2个波峰(图像的最高点,则正整数t的最小值是
A.5
B
6.在△ABC中，三内角A、B、C所对应的边长分别为a、b、c，且A、B、C成等差数列，
，则△ABC的外接圆半径为 A．
B
7.从5个男生、2个女生中任选派人,则下列事件中必然事件是 ( )
A.3个都是男生 B. 至少有1个男生
C.3个都是女生 D.至少有1个女生
8.某赛季甲、乙两面名篮球运动员每场比赛得分的茎叶图如下图所示:
| 甲 |
| 乙 |
| 8 6 4 3 8 6 3 9 8 3
1 | 0 1 2 3 3 4 5 4 5 | 2 5 4 5 1 1 6 6 7 9 4 9 0 |
则下列说法正确的是
A. 甲总体得分比乙好,且最高得分甲比乙高;
B. 甲总体得分比乙好,且最高得分乙比甲高;
C. 乙体得分比甲好,且最高得分乙比甲高;
D. 乙体得分比甲好,且最高得分甲比乙高;
9.已知点A(2,0),B(0,3),C(-1,-2),则
的顶点D的坐标为
A.(1,-5) B.(-3,1)
C.(1,-3) D.(-5,1)
10.在数列
中,a
=,
,则a
的值为
A.1002 B
11.下面的三视图(依次为正视图、侧视图、俯视图)表示的几何体是
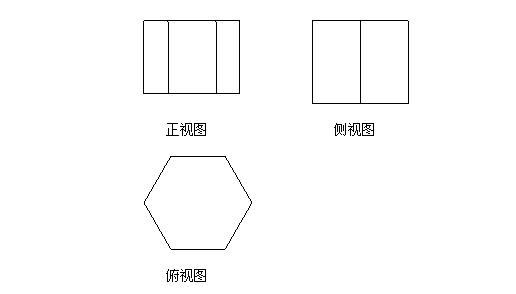
A.六棱柱 B.六棱锥 C.六棱台 D.六边形
12.若直线2x+3y+8=0,x-y-1=0和x+ky=0相交于一点,则k=
A.-
B.
C.-2 D.2
13.以点C(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆C的半径R的取值范围是
A.(0,20 ) B.(0,
)
C.(0,2)
D.(0,10)
14.若
与
互余,则
的值为
A.1 B
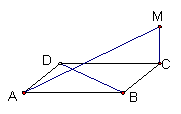
15.如图,如果MC⊥菱形ABCD所在的平面,那么MA与BD的位置关系是
A.平行, B.垂直相交
C.异面 D.相交但不垂直
16.圆锥平行于底面的截面面积是底面积的一半,则此截面分圆锥的高为上 、 下两段 的比为 A.
B.1:
.1:4
17.实数x、y满足不等式组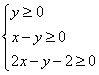 
,则
的取值范围 ( )
A.[-1,
] B.[-,] C.
D.
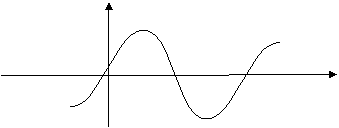
18.函数
的图像如图所示,则y的表达式为( )
|
A.
|
B. 
C. 
|
|
D. 
选择题 答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 得分 | |
| 答案 | ||||||||||
第II卷(非选择题共46分)
二、填空题(本大题共计4小题，每小题4分，共计16分，把答案填在题中横线上)
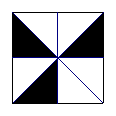19．如图所示，随机往正方形中扔一颗豆子（落在正方形外不算），则它落到阴影部分的概率是
20．某厂去年生产某种规格的电子元件a个，计划从今年开始的m年内，每年生产此种元件的产量比上一年增长p%，则此种规格电子元件年产量y随年数x的变化的函数关系是
21．某公司有1000名员工，其中，高层管理人员占50人，属高收入者；中层管理人员占200人，属中等收入者；一般员工占750人，属低收入者。要对这个公司员工的收入情况进行调查，欲抽取80名员工，则中层管理人员应抽取 人
22．若函数
唯一的一个零点同时在区间（0，16）、（0，8）、（0，4）、（0，2）内，下列结论：
（1）函数在区间（0，1）内有零点；
（2）函数在区间（0，1）或（0，2）内有零点；
（3）函数在区间[2，16]内无零点；
（4）函数在区间（1，16）内无零点。
其中正确的有 （写出所有正确结论的序号）。
三、解答题（本大题共3小题，每小题10分，共30分，解答应写出文字说明及演算步骤）
23．（本小题满分10分）已知函数
(1)用定义证明是偶函数；
(2)用定义证明在（—
，0）上是减函数；
(3)在所给坐标系中，作出函数的图像，并写出函数当x
[—1，2]时的最大值与最小值。
24．（本小题满分10分）
如图，在长方体
，已知底面两邻边
和
的长分别为3和4，对角线
与平面
所成的角为
，求：
（I） 长方体的高
；
（II） 长方体的表面积；
（III） 几何体
的体积。
25．（本小题满分10分）
某企业用银行无息贷款，投资280万元引进一条高科技生产流水线，预计第一年可获收入100万元，以后每年的收入增长10万元，但还需用于此流水线的保养维护费用每年45万元。
1) 若第
年该生产线的收入为
万元，年所获得总收入为
万元，求，
2) 求至少要多少年才能收回投资。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
参考答案
一：选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | A | C | A | C | B | B | D | A | C |
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 得分 | |
| 答案 | A | A | C | B | C | A | D | C |
二：填空题
19：
20：
21：16 22：（3）
三：解答题
23：（1），（2）略（3）最大值
，最小值
24：（1）高为5；（2）表面积94（平方单位）（3）体积30（立方单位）
25：（1）
，
（2）至少4年才能收回投资
说明：试卷是 画龙点睛 试卷一（合肥龙睛公司）2008.6.24