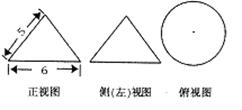
高二数学滚动测试题一2008.8.1
一:填空题(每题5分,共70分)
1、集合A={1,2,3,4},B={1,3,5,7},则A∩B= 。
2、幂函数y=xα在第一象限内恒过点 。
3、已知函数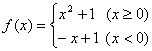 ,则
,则![]() =
。
=
。
4、函数y = lg (x – 1)的定义域为 。
5、在ΔABC中,角A、B、C的对边分别为a、b、c,且a2+b2=c2 –![]() ab,则∠C= 。
ab,则∠C= 。
6、已知向量![]() =(m – 1,– 4)与向量
=(m – 1,– 4)与向量![]() =(–3,4)共线,则实数m= 。
=(–3,4)共线,则实数m= 。
7、已知数列{ a n}的首项a1=![]() ,且满足
,且满足![]() (n∈N*),则a6= 。
(n∈N*),则a6= 。
8、已知各项均为正数的等比数列{ a n}中,a1•a89=16,则a44•a45•a46= 。
9、过点(–1,3)且与直线x – 2y + 3 = 0垂直的直线方程为 。
10、以点(–2,–4)为圆心,且与直线4x+3y – 10=0相切的圆的方程是 。
|
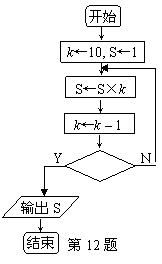
 12、若流程图所给的程序运行的结果为S=720,那么判断框中应填入的关于k的判断
12、若流程图所给的程序运行的结果为S=720,那么判断框中应填入的关于k的判断
条件是 。
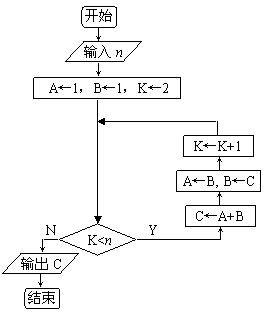
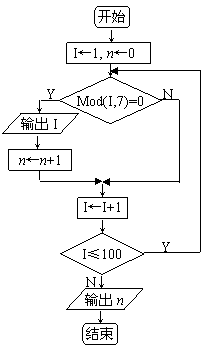
13、按下图所示流程图输入n=5,
 则输出的C=
。
则输出的C=
。
|
14、若不等式ax2+2ax – 4<2x2+4x对任意实数x均成立,则实数a的取值范围是 。
二:解答题(共六大题,共计90分)
15、(本题满分14分)
(1)已知函数y = x 2 – 2ax + 1在[1,2]上的最小值为g (a),试求g (a)的解析式;
(2)用条件语句描述求函数y = x 2 – 2ax + 1在[1,2]上的最小值的一个算法。
16、(本题满分14分)
在直四棱柱ABCD – A1B
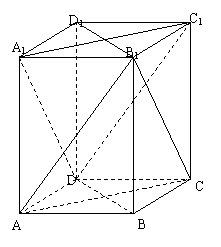 求证:(1)平面B
求证:(1)平面B
(2)平面B
17、(本题满分14分)已知函数f (x)=2acos2x + bsinxcosx,且f (0)=2, ![]() ;
;
(1)求函数f (x)的最大值与最小值;
(2)求函数f (x)的单调递增区间。
18、(本题满分14分)
设计一个算法,输出自然数1到100中能被7整除的数,并统计其个数。
(要求用自然语言写出算法,并画出流程图)
19、(本题满分18分)
小猴子摘了x个桃子,第一天吃了一半,觉得不过瘾,又吃了一个;第二天又吃了剩下的一半多一个;每天都如此;十天后剩下了1个桃子。记第10天剩下的桃子为a1、第9天剩下的桃子为a2、第8天剩下的桃子为a3、……、以此类推,这样a1、a2、a3、……构成一个数列{ a n}。
(1)试求a n与a n – 1 的关系式;
(2)求数列{ a n }的通项公式,并求x的值;
(3)试设计一个算法(用伪代码表示),并画出流程图。
20、(本题满分16分)
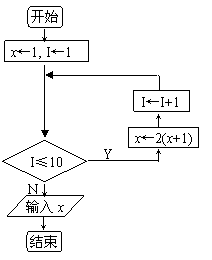
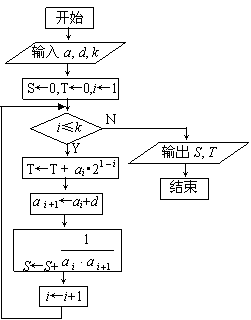 如图所示,流程图给出了无穷整数数列
如图所示,流程图给出了无穷整数数列![]() 满足的条件,
满足的条件,![]() ,且当k=5时,输出的S=
,且当k=5时,输出的S=![]() ;当k=10时,输出的S=
;当k=10时,输出的S=![]() 。
。![]()
(1)试求数列![]() 的通项公式
的通项公式![]() ;
;
(2)当k= n时,试求T的值。
![]()
高二数学滚动测试题一参考答案
一:填空题
1、{1,3} 2、(1,1) 3、– 5 4、(1,+∞) 5、150o 6、4 7、![]() 8、64
8、64
9、2x+y
– 1=0 10、(x+2)2+(y+4)2=36 11、12![]() 12、k≤7或k<8 13、5 14、
12、k≤7或k<8 13、5 14、![]()
二:解答题
15、解:(1)当a≤1时,函数在[1,2]上单调递增,则x=1时,y取最小值,
所以g(a)=2–
当a∈[1,2]时,函数在[1,a]上单调递减,在[a,2]上单调递增,所以x=a时,
y取最小值,所以g (a)=1 – a 2; …………2分
当a≥2时,函数在[1,2]上单调递减,所以x =2时,y取最小值,
所以g (a)=5
–
所以,g (a)=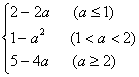 …………2分
…………2分
|
…………4分
16、证明(1)因为ABCD – A1B
而A![]() 平面B
平面B![]() 平面B
平面B
同理,A1D∥平面B
因为A![]() 平面DC
平面DC
(2)因为ABCD – A1B
而AC![]() 平面ABCD,所以AC⊥B1B,因为底面ABCD是菱形,所以AC⊥BD,
平面ABCD,所以AC⊥B1B,因为底面ABCD是菱形,所以AC⊥BD,
因为B1B、BD![]() 平面B1BDD1,B1B∩BD=B,所以AC⊥平面B1BDD1…………12分
平面B1BDD1,B1B∩BD=B,所以AC⊥平面B1BDD1…………12分
因为AC![]() 平面B
平面B
17、解:(1)∵f (0)=2cos20+bsin0cos0=
∵![]() , ∴b=2 …………3分
, ∴b=2 …………3分
(2)由(1)知 f (x)=2cos2x + 2sinxcosx=1+cos2x+sin2x=![]() …………3分
…………3分
∴f (x)max= ![]() +1, f (x)min=
+1, f (x)min= ![]() – 1
…………2分
– 1
…………2分
![]()
∴![]() ,
,![]()
 ∴函数f (x)的单调递增区间为
∴函数f (x)的单调递增区间为![]() 。
…………3分
。
…………3分
|
19、解:(1)由题意知:a n – 1 =![]() a n
– 1,
a n
– 1,
a n =
 (2)由(1)知:a n +2=2(a n – 1 +2)
(2)由(1)知:a n +2=2(a n – 1 +2)
所以{ a n +2}构成以a 1+2=3为首项,
公比为2的等比数列,…………2分
所以a n =3•2n – 1 – 2 …………2分
|
伪代码:
…………4分 ……4分
20、解(1)由题设知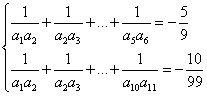 …………4分
…………4分
又![]() 是等差数列,设公差为d,
是等差数列,设公差为d,
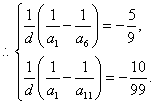 即
即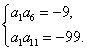 …………3分
…………3分
两式相减得:![]()
又![]() ,
,![]() 舍,
舍,
![]() …………2分
…………2分
(2)![]() ①
…………2分
①
…………2分
①式两边同乘![]() 得
得![]() ② …………2分
② …………2分
②-①得![]()
![]() =
=![]()
![]() .
…………3分
.
…………3分