高二数学直线和圆的方程单元测试(直线和圆的方程⑴)
班级 学号 姓名
一.选择题(3 ![]() 12).
12).
1.下列命题正确的是( )
A.若直线的斜率存在,则必有倾斜角α与它对应 ;B.若直线的倾斜角存在,则必有斜率与它对应;
C.直线的斜率为k,则这条直线的倾斜角为arctank; D.直线的倾斜角为α,则这条直线的斜率为tanα .
2.过点![]() 与
与![]() 的直线
的直线![]() 的倾斜角为( )
的倾斜角为( )
A.![]() B.
B.![]() C.
C.![]()
![]() D.
D.![]()
3.过点![]() 的直线的倾斜角为
的直线的倾斜角为![]()
![]() ,则实数
,则实数![]() 的值为( )
的值为( )
A.2 B.
4.直线![]() 的倾斜角的范围是( )
的倾斜角的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.下列说法中不正确的是( )
A.点斜式![]() 适用于不垂直于x轴的任何直线
适用于不垂直于x轴的任何直线
B.斜截式![]() 适用于不垂直于x轴的任何直线
适用于不垂直于x轴的任何直线
C.两点式![]() 适用于不垂直于x轴和y轴的任何直线
适用于不垂直于x轴和y轴的任何直线
D.截距式![]() 适用于不过原点的任何直线
适用于不过原点的任何直线
6.过点![]() 的直线与x、y轴分别交于P、Q,若M为线段PQ的中点,则这条直线的方程为
的直线与x、y轴分别交于P、Q,若M为线段PQ的中点,则这条直线的方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.直线![]() 到直线
到直线![]() 的角为 ( )
的角为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.直线![]() 与直线
与直线![]() 互相垂直,
互相垂直,![]() R,则
R,则![]() 的最小值为 ( )
的最小值为 ( )
A.1 B.
9.已知点(2,-1)和(-3,2)在直线![]() 的异侧,则
的异侧,则![]() 的取值范围是( )
的取值范围是( )
A.(4,7) B.(-4,7) C.(-7,4) D.(-4,4)
10.若点A(4,a)到直线4x-3y-1=0的距离不大于3,则 ( )
A.-1<a<9 B.0≤a≤
11.已知点P(-1,1)、Q(2,2),若直线L:![]() 与线段PQ的延长线相交,则m的取值范围为( )
与线段PQ的延长线相交,则m的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
12.若动点![]() 、
、![]() 分别在直线
分别在直线![]() 上移动,则线段AB的中点M到原点的距离的最小值为(
)
上移动,则线段AB的中点M到原点的距离的最小值为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题:(3 ![]() 5)
5)
13.过点A(4,1)且在两坐标轴上的截距互为相反数的直线的方程是
14. 一条直线过点![]() ,且与两坐标轴围成的三角形的面积为
,且与两坐标轴围成的三角形的面积为![]() 的直线的方程为
的直线的方程为
15.已知实数![]() 、
、![]() 满足
满足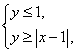 则
则![]() 的最大值是
的最大值是
16.不等式组 所表示的平面区域的面积是 _____________;
所表示的平面区域的面积是 _____________;
17.已知两直线![]() :
:![]() ,
,![]() :
:![]() ,当这两条直线的夹角在区间
,当这两条直线的夹角在区间![]() 内变化时,
内变化时, ![]() 的取值范围是
.
的取值范围是
.
三.解答题:
18.(9分) 直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,把直线
,把直线![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() ,求得到的直线方程。
,求得到的直线方程。
19.(10分)已知![]() 的顶点A(3,-1),过点B的内角平分线的方程是
的顶点A(3,-1),过点B的内角平分线的方程是![]() ,过点C的中线方程为
,过点C的中线方程为![]() .求直线BC的方程.
.求直线BC的方程.
20. (10分) 已知等腰直角三角形的斜边所在直线方程是:![]() ,直角顶点
,直角顶点![]() (
(![]() ),求两条直角边所在的直线方程和此三角形面积.
),求两条直角边所在的直线方程和此三角形面积.
21. (10分) 营养学家指出,成人良好的日常饮食应该至少提供
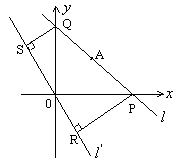 22. (10分)已知过点
22. (10分)已知过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,过
两点,过![]() 作直线
作直线![]() 的垂线,垂直分别为
的垂线,垂直分别为![]() (如图);求四边形
(如图);求四边形![]() 面积的最小值和此时直线
面积的最小值和此时直线![]() 的方程。
的方程。
附加题:(20分)已知函数![]() ,函数
,函数![]() 的图象与
的图象与![]() 的图象关于点(1,2)对称. ① 求
的图象关于点(1,2)对称. ① 求![]() 的解析式;② 解关于
的解析式;② 解关于![]() 的不等式:
的不等式:![]() .
.
答案
一.ADBBD CDBBB AC
二.13:![]() 或
或![]() 14:
14:![]() 15: 4 17:
15: 4 17:![]()
16.解:由![]() 得交点
得交点![]() ,从而所表示的平面区域的面积是
,从而所表示的平面区域的面积是![]()
三.解答题:
18. 解:易求得点M的坐标为(2,0)。设![]() 的斜率为k,倾斜角为α,则tanα=k=2 由题知旋转后的直线的倾斜角为α+45°,斜率为tan(α+45°)∴tan(α+45°)=k′=
的斜率为k,倾斜角为α,则tanα=k=2 由题知旋转后的直线的倾斜角为α+45°,斜率为tan(α+45°)∴tan(α+45°)=k′=![]() =-3∴所求直线的方程为y-0=-3(x-2) 即为3x+y-6=0
=-3∴所求直线的方程为y-0=-3(x-2) 即为3x+y-6=0
19.解:设B(m,n),由过B的平分线方程得![]() ,又
,又![]() AB中点
AB中点![]() 在过C的中线上,
在过C的中线上,
∴![]() ,由
,由 得
得![]() ,则B(10,5).又
,则B(10,5).又![]()
![]() ,过点B的角平分线的斜率
,过点B的角平分线的斜率![]() ,
,![]()
![]() ,∴BC的方程为
,∴BC的方程为![]() ,即
,即![]()
20. 解:∵直线AB方程为3x-y+2=0 ∴KAB=3设与直线AB成45°角的直线斜率为k,则![]()
解之得:k=![]() 或k=-2 故两直角边所在直线方程为:x-2y-2=0和2x+y-6=0
由于点C到AB的距离d=
或k=-2 故两直角边所在直线方程为:x-2y-2=0和2x+y-6=0
由于点C到AB的距离d=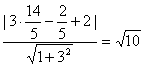 而AB=2d=2
而AB=2d=2![]() ∴所求三角形面积为S=
∴所求三角形面积为S=![]()
21.解:设每天食用x kg食物A,y kg食物B,总成本为z,那么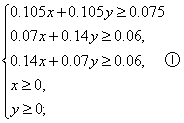
目标函数为z=28x+21y.二元一次不等式组①等价于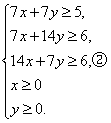
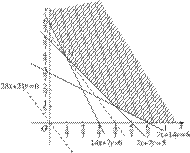
作出二元一次不等式组②所表示的平面区域,如下图阴影部分即可行域.
如图所示,当直线z=28x+21y经过可行域上的点M时,截距最小,即z最小.
解方程组![]() ,得M的坐标为
,得M的坐标为![]() ,
,![]() . 所以z min=28x+21y=16.
. 所以z min=28x+21y=16.
由此可知,每天食用食物A约
22.解1:∵![]() 及直线
及直线![]() 的斜率为
的斜率为![]() , ∴直线
, ∴直线![]() 为:
为:![]() ,即
,即![]()
∴![]() ,
,![]() 又∵
又∵![]() ∵
∵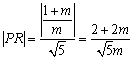 ,
,![]()
 ∵直线
∵直线![]() ,即
,即![]() ∴
∴![]()
∴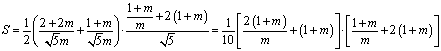
![]()
![]() (当且仅当
(当且仅当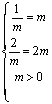 ,即
,即![]() 时取“
时取“![]() ”)
”)
故: ![]() ,此时直线
,此时直线![]() 的方程为:
的方程为:![]() ,
, ![]()
解2:可设直线![]() 的方程为:
的方程为:![]() ,则
,则![]()
∴直线![]() 为:
为:![]() ,即
,即![]() 于是
于是![]() ,
,![]()
又∵直线![]() ,即
,即![]() ∴
∴![]()
∴![]()
∵直线![]() 过点
过点![]() ∴
∴![]() ∴
∴![]() ,
,![]() ,
,![]()
(当且仅当 ,即
,即![]() 时取“
时取“![]() ”)
”)
∴![]() ,此时直线
,此时直线![]() 的方程为:
的方程为:![]() ,即
,即![]()
附加题:解:①设![]() 图象上的点,它关于(1,2)的对称点为
图象上的点,它关于(1,2)的对称点为![]()
则 ![]() ,∵
,∵ ![]() 上 ∴
上 ∴
![]() ,即有
,即有 ![]()
即 ![]()
② 由已知有 ![]() ∴
∴ ![]() ,即
,即 ![]()
∴ ![]() 或
或
![]() ∴
∴ 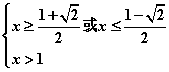 或
或
![]()
∴
不等式解集为![]()