高二数学第二学期期末模拟试卷

高二数学第二学期期末模拟试卷

一、填空题

1．完成下面的三段论：　　　　　　　　　大前提：互为共轭复数的乘积是实数

小前提：与是互为共轭复数　　结　论：　　　　　　　　　　　　

是实数

2、设P为曲线C：上的点，且曲线C在点P处切线倾斜角的取值范围为，则点P横坐标的取值范围为_______。[-1，-]

3．已知如下结论：“等边三角形内任意一点到各边的距离之和等于此三角形的高”，将此结论拓展到空间中的正四面体（棱长都相等的三棱锥），可得出的正确结论是：　　　　　

　　　　　　　　　　　 正四面体体内任意一点到各面的距离之和等于此正四面体的高。

4．从4位男教师和3位女教师中选出3位教师，派往郊区3所学校支教，每校1人，要求这3位教师中男、女教师都要有，则不同的选派方案有　　　　种（用数字作答）180

5．设随机变量~，且，则　　　　  。2m-1

6．已知,则( 的值等于　　　　  。-256

7．通过随机询问250名不同性别的大学生在购买食物时是否看营养说明书，得到如下2×2联表：

	女	男	总计
读营养说明书	90	60	150
不读营养说明书	30	70	100
总计	120	130	250

从调查的结果分析，认为性别和读营养说明书的有关的可能性在___________以上。99.9%

8．抛掷一颗质地均匀的骰子，将向上一面的点数看作随机变量X，则X的方差是　　． 

9．从一副不含大小王的52张扑克牌中不放回地抽取2次，每次抽1张，已知第1次抽到A，那么第2次也抽到A的概率为_______． 

10．函数在（0，2）内的单调增区间为　 　　 　．［，］

11．设z=x+yi（），且的最小值是_________．

12、在的展开式中，含x的系数为　　　　　 　　　　 ．-9

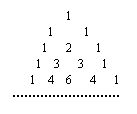13．如右图，在杨辉三角形中，

从上往下数共有n(n∈N^*)行，

在这些数中非1的数字之和为　　　　　　　  2ⁿ-2n

14．函数由下表定义：

x	1	2	3	4	5
f (x)	3	4	5	2	1

若，,则的值________________．1

二、解答题

15．已知为复数，.

解：设则

为纯虚数

于是x=3y　

∴y=5　即y=±5　

故

16．在一次面试中，每位考生从4道题a,b,c,d中任抽两题做，假设每位考生抽到各题的可能性相等，且考生相互之间没有影响．

（1）若甲考生抽到a,b题，求乙考生与甲考生恰好有一题相同的概率；

（2）设某两位考生抽到的题中恰好有X道相同，求随机变量X的概率分布和期望E(X)．

解：（1）

答：乙考生与甲考生恰有一题相同的概率为．

（2）的可能取值为　

　　  ，

所以随机变量的概率分布为

　

X	0	1	2
P	1/6	2/3	1/6

的期望

17．某电脑公司有6名产品推销员，其工作年限与年推销金额数据如下表:

推销员编号	1	2	3	4	5
工作年限/年	3	5	6	7	9
推销金额/万元	2	3	3	4	5

(Ⅰ)求年推销金额与工作年限x之间的相关系数；

(Ⅱ)求年推销金额关于工作年限的线性回归方程；

(Ⅲ)若第6名推销员的工作年限为11年，试估计他的年推销金额.

（参考数据：；由检验水平0.01及,查表得.）

解： (Ⅰ)由=10，20，5.2，

　　 可得.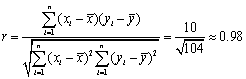

∴年推销金额与工作年限x之间的相关系数约为0.98．　　

(Ⅱ) 由(Ⅰ)知，,

　　 ∴可以认为年推销金额与工作年限x之间具有较强的线性相关关系.

设所求的线性回归方程为，

则，.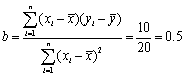

∴年推销金额关于工作年限的线性回归方程为.　

　 (Ⅲ) 由(Ⅱ) 可知,当时,

万元.

∴可以估计第6名推销员的年推销金额为5.9万元．　

18．已知a+b+c=0且a>b>c。求证：

证明：∵a+b+c=0且a>b>c　　

∴a>0，c<0

<a

b²-ac<3a²

（-a-c）²-ac<3a²

2 a²-ac-c²>0

（2a+c）（a-c）>0

∵a>0，c<0

∴a-c>0

∵a+b+c=0且a>b

∴a>-a-c即2a+c>0

∴（2a+c）（a-c）>0成立

故原不等式得证。

19．已知a_n=4n+5，b_n=3ⁿ，求证：对任意正整数n，都存在正整数p，使得a_p= 成立．

解法一：①当时，，即存在，使，结论成立；

②假设当（）时，存在正整数，使，即成立．

∴当时，存在正整数，使得，即当时，结论成立。

由①②可得，对，存在正整数，使.

法二：∵

，

又，∴

∴对任意正整数，存在，使。

20．已知是实数，函数。

（Ⅰ）若，求的值及曲线在点处的切线方程；

（Ⅱ）求在区间上的最大值。

解：（Ⅰ），

因为，

所以．

又当时，，，

所以曲线在处的切线方程为．

（Ⅱ）解：令，解得，．

当，即时，在上单调递增，从而

．

当，即时，在上单调递减，从而

．

当，即时，在上单调递减，在上单调递增，从而

综上所述，