高二数学第二学期期末考试

高二数学第二学期期末考试

一．填空题（每小题5分，共70分）

1．　已知全集I=N,集合A={1,2,3,4,5,6}, B={2,3,5},则=____▲_____；

2．　函数f(x)=的定义域是_____▲______；

3．　计算= 　　　　　  ▲　　　　  ；

　　　　　

4．计算sin(-570°)的值是____▲____；

5．已知直线l：x－2y=0和l：x+3y=0，则直线l和l的夹角是　　 ▲　　  ；

6．如果logm＋logn＝4，那么m＋n的最小值是　　  ▲　　　　；

7．已知三角形的顶点为A（2，4）、B（1，－2）、C（－2，3）则BC边上的高AD所在直线的方程是　　　　　   ▲　　　　　　  ；

　　　　　　　　　　　　 

8．在等比数列｛a｝中，a＞0，aa+2aa+aa＝25，

则a＋a＝　　　▲　　  ；

　　　　　 

9．设a=0.3，b=2，c=log2，则a、b、c的大小关系

是　　　 　 ▲　　　　；

　　　　　　　　　 

10．若数列﹛a﹜的前n项由流程图（右图所示）的输出依次给出，

则数列的通项公式a＝　　　  ▲　　　　；

11．直线与曲线相切于点，

则b的值为____▲____；

　　　　　　　　 

12．关于直线 m、n 和平面 a、b 有以下四个命题：

① 当 m∥a ，n∥b ，a∥b 时，m∥n，

② 当 m∥n，m Ì a ，n⊥b 时，a⊥b，
③ 当 a∩b = m，m∥n 时，n∥a 且 n∥b，　

④ 当 m⊥n，a∩b = m时，n⊥a 或n⊥b。
其中假命题的序号是______▲________；

　　　　　　　 

13．已知sin－cos=m－1，则实数m的取值范围是　　　  ▲　 　　 ；

　　　　　　　　　　 

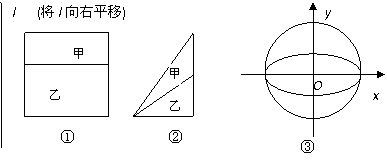
14．我们可以运用下面的原理解决一些相关图形的面积问题：如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k，那么甲的面积是乙的面积的k倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是与，运用上面的原理，图③中椭圆的面积为　 ▲　 。

 

 

 

 

二．解答题（本大题共六小题，满分90分）

15．（本题满分14分）

设锐角三角形ABC的内角A、B、C的对边分别为a、b、c，a＝2bsinA。

（1）　　　 求角B的大小；

（2）　　　 若a＝3，c＝5，求b的值。

16．（本题满分14分）

已知向量，，记．

（1）求f(x)的解析式并指出它的定义域；

（2）若，且，求．

17． （本题满分15分）

如图，直四棱柱ABCD—A₁B₁C₁D₁的高为3，底面是边长为4且∠DAB=60°的菱形，AC∩BD=0，A₁C₁∩B₁D₁=O₁，E是O₁A的中点.

（1）求二面角O₁－BC－D的大小；

（2）求点E到平面OBC的距离.

　　　　　　　　　　　　　　　　　　　　　　　

18．(本题满分15分)

某人抛掷一枚硬币，出现正反的概率都是，构造数列，

使，记

（1）求时的概率；

（2）求恰有2次连续出现2次反面且时的概率。

19．（本题满分16分）

统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升）关于行驶速度（千米/小时）的函数解析式可以表示为：已知甲、乙两地相距100千米。

（1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

（2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

20．（本题满分16分）

已知直线与圆交于不同点A_n、B_n,其中数列满足：.

（1）求数列的通项公式；

（2）设求数列的前n项和。

高二（下）数学期末考试答案

三．填空题（每小题5分，共70分）

1．{1，4，6}　　　 2．X＜　　　 3． 　　　4． 　　　5．

6．18　　 7．3x－5y+14=0　　　8．5　　　9．a＜b＜c　　　　10．n(n+1)

11．3　　　12．①③④　　 13．－1≤m≤3　　　14．ab

四．解答题（本大题共六小题，满分90分）

15．（本题满分14分）

（1）由a=2bsinA得，＝2sinA，sinB＝，又B锐角，∴B＝

　　（2）由B＝得cosB＝，∴b＝a＋c－2accosB

＝27＋25－2×3×5× ＝7，　∴b＝

16．（本题满分14分）

（1）由f(x)=a·b=（1－tanx）(1+sin2x+cos2x)=2cos2x，∴f(x)．

定义域为．

（2）∵f(+)=2cos(2+)，∴cos(2+)＝，又∈（0，），∴cos2=，cos2＝－（舍），∴f()=2 cos2=

17． （本题满分15分）

（1）过O作OF⊥BC于F，连接O₁F，

∵OO₁⊥面AC，∴BC⊥O₁F，

∴∠O₁FO是二面角O₁－BC－D的平面角

∵OB=2，∠OBF=60°，∴OF=.

在Rt△O₁OF在，tan∠O₁FO=∴∠O₁FO=60°

即二面角O₁—BC—D为60°　　

（2）在△O₁AC中，OE是△O₁AC的中位线，∴OE∥O₁C

∴OE∥O₁BC，∵BC⊥面O₁OF，∴面O₁BC⊥面O₁OF，交线O₁F.

　 过O作OH⊥O₁F于H，则OH是点O到面O₁BC的距离，

点E到面O₁BC的距离等于OH，

　 ∴OH=∴点E到面O₁BC的距离等于

18．(本题满分15分)

（1）

（2）

19．（本题满分16分）

（1）若千米/小时，每小时耗油量为升/小时.

共耗油升.

所以，从甲地到乙地要耗油17.5升.

（2）设当汽车以千米/小时速度匀速行驶时耗油量最少，，耗油量为S升.

则，

，

令，解得，.

列表：

		极小值11.25

所以，当汽车以80千米/小时的速度匀速行驶时，耗油量最少，为11.25升.

20．（本题满分16分）

（1）圆心到直线的距离，

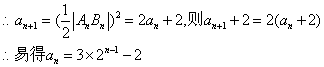
（2）　　

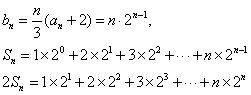
两式相减得，